|
| | Le dernier jeu pour la préparation aux IMOs 2012: |  |
|
+14alidos Ahmed Taha (bis) Maths_BT amigo-6 darkpseudo Coulomb yasserito momo1729 boubou math Mehdi.O az360 diablo902 Oty nmo 18 participants | |
| Auteur | Message |
|---|
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 09 Mar 2012, 23:45 Ven 09 Mar 2012, 23:45 | |
| Bravo , a toi de Proposé .... | |
|   | | az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 09 Mar 2012, 23:47 Ven 09 Mar 2012, 23:47 | |
| on passe maintenant au combinatoire !!
Probleme 7 :
une feuille de papier est déchirée en trois parties . ensuite l'une de ces parties est déchériée de nouveau en 3 parties . est ainsi de suite . peut-on oubtenir a fin de compte un total de cent parties ?
| |
|   | | diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 09 Mar 2012, 23:53 Ven 09 Mar 2012, 23:53 | |
| - az360 a écrit:
- on passe maintenant au combinatoire !!
Probleme 7 :
une feuille de papier est déchirée en trois parties . ensuite l'une de ces parties est déchériée de nouveau en 3 parties . est ainsi de suite . peut-on oubtenir a fin de compte un total de cent parties ?
Solution du 7:Au début, on a une feuille, notons une étape =x après 1x on aura 5 après 2x on aura 7 après nx on aura 3+2n =1 la réponse est NON | |
|   | | diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Sam 10 Mar 2012, 00:03 Sam 10 Mar 2012, 00:03 | |
| Problème 8:ABC est un triangle (BC<AC).M est le milieu de [AB].AP(res.BQ) est la hauteur issue de A(res.B) (dans le triangle ABC). Supposons que (QP) coupe (AB) dans T.Si H est l'orthocentre du triangle ABC,prouver que &space;\perp&space;(CM)}) | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Sam 10 Mar 2012, 21:23 Sam 10 Mar 2012, 21:23 | |
| Solution au problème 8:On note R l'intersection des cercles cironscrits de PHQ et AHB. M est clairement le centre du cercle passant par A,B,P et Q. On a donc : angle{BRP}=360-angle{PRQ}-angle{ARQ}-angle{BRA}=360-angle{PHQ}-(angle{HPQ}+angle{HPQ})-angle{PHQ}=2angle{BAP}=angle{BMP} ainsi le quadrilatère BMRP est cyclique de même AMRQ l'est. Donc par le théorème des axes radicaux on obtient le fait que R est l'intersection de TH et MC et ainsi puisque le quadrilatère PHQC est cylique on a angle{CRH}=angle{HPC}=90, ce qui donne le résultat voulu. Problème 9 : Soit a>2, et définissions : :a_{n+1}=(\frac{a_n^2}{a_{n-1}^2}-2)a_n) . Prouver que : :\sum_{i=0}^{k}\frac{1}{a_i}<&space;\frac{1}{2}(2+a-\sqrt{a^2-4})) . | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mer 14 Mar 2012, 18:21 Mer 14 Mar 2012, 18:21 | |
| Bonjour , je pense enfin avoir réussi ( Hamdoullillah ) a Prouver le jolie problème proposé par Diablo , je propose cette démonstration alternative : soit N , l'intersection de (TH) et (CM) , E l'intersection de (TH) et (BP) , I la projection orthogonale de M sur (BP) , par thales on a I est le milieu de [BP] . Pour prouver que les deux droites sont perpendiculaire il suffit de prouver que le quadrilatère HNQC est inscriptible , ce qui revient a montrer que les angles NCQ=x et NHQ=y sont égaux (x=y) . Pour ce faire , il suffit de démontrer que tan(x)=tan(y) ou encore pour ce faciliter la tanche , tan(C-x)=tan(C-y) , (car on remarque que l'angle BHP=AHQ=C et EHP=C-x) , avec l’intervention du point I , on parvient facilement a calculer tan(C-y) en fonction de paramètres fixes , on trouve : =\frac{tan(C)tan(B)}{tan(C)+2tan(B)}) , cependant en ce qui concerne le calcule de tan(C-x) c'est bien plus ardu .... On constate sur la figure que les points T,P,Q sont alignés ainsi que les points T,E et H , en combinant les deux égalités obtenue en appliquant le théorème de Ménélaus au triangles ABC et BAP , en parvient a isolé la variable BE (qui nous manque pour calculer tan(C-y) dans le triangle BHP rectangle en P ) et a l'exprimer en fonction de ces même paramètre fixe , on trouve }{tan(C)+2tan(B)}) , d'ou )=(\frac{BP}{HP}).(\frac{tan(B)}{tan(C)+2tan(B)})=\frac{tan(C)tan(B)}{tan(C)+2tan(B)}&space;.) , ce qui achève la démonstration ... sauf erreur . | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 16 Mar 2012, 13:12 Ven 16 Mar 2012, 13:12 | |
| - Mehdi.O a écrit:
- Problème 9 :
Soit a>2, et définissions :
:a_{n+1}=(\frac{a_n^2}{a_{n-1}^2}-2)a_n)
. Prouver que :
:\sum_{i=0}^{k}\frac{1}{a_i}<&space;\frac{1}{2}(2+a-\sqrt{a^2-4})) . . Je propose une suite de ce que j'ai avancé ultérieurement: une démonstration pénible. Un résultat préliminaire:La condition initiale  fait rappel à l'inégalité arithmético-géométrique, car on se souvient bien que  : x+\frac{1}{x}>2) . Je profite de cette persuasion pour écrire  tel que x est un réél positif strictement supérieur à 1. On écrit ainsi  ,  et (x^2+\frac{1}{x^2})) . On peut conjecturer que :a_n=(x+\frac{1}{x})(x^2+\frac{1}{x^2})\cdots(x^{2^{n-1}}+\frac{1}{x^{2^{n-1}}})=\prod_{m=0}^{n-1}(x^{2^m}+\frac{1}{x^{2^m}})) . Et on peut apporter à ce résultat une preuve en utilisant tout simplement une récurrence facile. De plus, on a :\frac{1}{a_n}=\frac{1}{(x+\frac{1}{x})(x^2+\frac{1}{x^2})\cdots (x^{2^{n-1}}+\frac{1}{x^{2^{n-1}}})}) . Ce qui peut s'écrire comme: :\frac{1}{a_n}=\frac{x.x^2\cdots x^{2^{n-1}}}{(x^2+1)(x^4+1)\cdots (x^{2^n}+1)}) . Mais, puisqu'on a :1+2+2^2+\cdots+2^{n-1}=2^n-1) . Il résulte que :\frac{1}{a_n}=\frac{x^{2^n-1}}{(x^2+1)(x^4+1)\cdots (x^{2^n}+1)}) . Revenons à l'inégalité:Je commence par simplifier le côté droit de l'inégalité: On a =\frac{1}{2}\big(2+x+\frac{1}{x}-\sqrt{x^2+\frac{1}{x^2}-2}\big)=\frac{1}{2}\big(2+x+\frac{1}{x}-\sqrt{(x-\frac{1}{x})^2}\big)=\frac{1}{2}\big(2+x+\frac{1}{x}-x+\frac{1}{x}\big)=\frac{1}{2}(2+\frac{2}{x})) . (car x est supérieur à 1) En résumé: =1+\frac{1}{x}) . L'inégalité à démontrer devient équivalente à :1+\frac{x}{x^2+1}+\cdots+\frac{x^{2^k-1}}{(x^2+1)(x^4+1)\cdots (x^{2^k}+1)}<1+\frac{1}{x}) . Ou encore à :\frac{x^2}{x^2+1}+\cdots+\frac{x^{2^k}}{(x^2+1)(x^4+1)\cdots (x^{2^k}+1)}<1) . Il suffit de voir que :\frac{x^{2^n}}{(x^2+1)(x^4+1)\cdots (x^{2^n}+1)}=\frac{x^{2^n}+1-1}{(x^2+1)(x^4+1)\cdots (x^{2^n}+1)}}=\frac{x^{2^n}+1}{(x^2+1)(x^4+1)\cdots (x^{2^n}+1)}-\frac{1}{(x^2+1)(x^4+1)\cdots (x^{2^n}+1)}}) . C'est à dire :\frac{x^{2^n}}{(x^2+1)(x^4+1)\cdots (x^{2^n}+1)}=\frac{1}{(x^2+1)(x^4+1)\cdots (x^{2^{n-1}}+1)}}-\frac{1}{(x^2+1)(x^4+1)\cdots (x^{2^n}+1)}}) . En sommant les inégalités membre par membre, en allant de l'entier 1 à l'entier k, on trouve que :\frac{x^2}{x^2+1}+\cdots+\frac{x^{2^k}}{(x^2+1)(x^4+1)\cdots (x^{2^k}+1)}=\frac{1}{x+1}-\frac{1}{(x^2+1)(x^4+1)\cdots (x^{2^k}+1)}) . Ainsi, il suffit de montrer que :\frac{1}{x+1}-\frac{1}{(x^2+1)(x^4+1)\cdots (x^{2^k}+1)}<1) . La dernière inégalité se démontre facilement, en posant 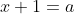 et :(x^2+1)(x^4+1)\cdots (x^{2^k}+1)=b_k) . En effet, elle équivaut à :b_k<a(b_k+1)) . Ce qui est trivialement vrai, car :b_k<b_k+1) et  . D'où le résultat. CQFD. Sauf erreur.
Dernière édition par nmo le Ven 16 Mar 2012, 13:21, édité 1 fois | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 16 Mar 2012, 13:20 Ven 16 Mar 2012, 13:20 | |
| Problème 10:Soit I le centre du cercle inscrit dans un triangle ABC. Soient D, E et F les pieds des bissectrices (AI), (BI) et (CI). Soient X, Y et Z trois points quelquonques sur les segments [EF], [FD] et [DE] respectivement. Montrez que )+d(Y,(BC))+d(Z,(CA))\le XY+YZ+ZX) . Où )) est la distance entre le point M et la droite (D). Bonne chance. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Lun 19 Mar 2012, 12:24 Lun 19 Mar 2012, 12:24 | |
| - nmo a écrit:
- Problème 10:
Soit I le centre du cercle inscrit dans un triangle ABC.
Soient D, E et F les pieds des bissectrices (AI), (BI) et (CI).
Soient X, Y et Z trois points quelquonques sur les segments [EF], [FD] et [DE] respectivement.
Montrez que )+d(Y,(BC))+d(Z,(CA))\le XY+YZ+ZX) . .
Où )) est la distance entre le point M et la droite (D). est la distance entre le point M et la droite (D).
Bonne chance. Cela fait longtemps que le problème est ici sans solution. Je propose la mienne, espérant qu'elle soit juste et sans erreurs: Faites attention, car je vais utiliser plusieurs notations: On note )) , ) et )) . On note aussi )) , ) et )) . On défini finalement  la hauteur du trapèze dont les bases ont pour longueurs  et  . De même, on défini  et  . (Remarquez que D appartient au segment de longueur  , et respectivement pour les autres). Il est aisé de voir que ^2) , ^2) et que ^2) . Il est facile de voir à l'aide de l'inégalité de Caushy-Schwartz que (c-\gamma))^2\le (f^2+(c-\gamma)^2)(d^2+(a-\alpha)^2)) . C'est à dire que  . De même, on minimise les deux autres produits  et  . On aura en sommant ces trois inégalités et en ajoutant  , le résultat important suivant: +\sum_{cyc}(ac)+\sum_{cyc}(\alpha.\gamma)-(\sum_{cyc}a)(\sum_{cyc}\alpha)\le\sum_{cyc}(XY.YZ)-c.\gamma-a.\alpha-b.\beta) . C'est à dire que +2\sum_{cyc}(ac)+2\sum_{cyc}(\alpha.\gamma)-2(\sum_{cyc}a)(\sum_{cyc}\alpha)\le2\sum_{cyc}(XY.YZ)-2c.\gamma-2a.\alpha-2b.\beta) . Et ainsi +\sum_{cyc}a^2+2\sum_{cyc}(ac)+\sum_{cyc}\alpha^2+2\sum_{cyc}(\alpha.\gamma)-2(\sum_{cyc}a)(\sum_{cyc}\alpha)\le2\sum_{cyc}(XY.YZ)+f^2+c^2-2c.\gamma+\gamma^2+d^2+a^2-2a.\alpha+\alpha^2+e^2+b^2-2b.\beta+\beta^2) . Donc ^2+(\sum_{cyc}a)^2+(\sum_{cyc}\alpha)^2-2(\sum_{cyc}a)(\sum_{cyc}\alpha)\le2\sum_{cyc}(XY.YZ)+f^2+(c-\gamma)^2+d^2+(a-\alpha)^2+e^2+(b-\beta)^2=2\sum_{cyc}(XY.YZ)+\sum_{cyc}(XY^2)) . Ce qui équivaut à ^2+(\sum_{cyc}a-\sum_{cyc}\alpha)^2\le(\sum_{cyc}XY)^2) .==>(1) Je vais compléter la solution plus tard... La porte est ouverte à n'importe quel membre pour compléter la solution, ou chercher une solution alternative. Afin de ne pas bloquer le jeu, je proposerai dans un instant un autre problème. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mer 21 Mar 2012, 20:10 Mer 21 Mar 2012, 20:10 | |
| J'ai édité l'ancien problème d'arithmétiques que j'ai proposé: Problème 11:Trouvez toutes les fonctions 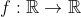 qui satisfont la relation suivante: \in\mathbb{R}^2):f(f(x+y).f(x-y))=x^2-y.f(y)) . Bonne chance. | |
|   | | boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mer 21 Mar 2012, 21:43 Mer 21 Mar 2012, 21:43 | |
| Solution du Problème 11Considérons l'assertion : :f(f(x+y).f(x-y))=x^2-yf(y)) ainsi : :f(f(y).f(-y))=-yf(y)) et aussi :f(f(y).f(-y))=yf(-y)) on conclue que pour y non nul =-f(-y)) d'une autre part: :f(f(x+y).f(y-x))=y^2-xf(x)\Rightarrow&space;f(-f(x+y).f(x-y))=y^2-xf(x)\Rightarrow&space;-f(f(x+y).f(x-y))=y^2-xf(x)\Rightarrow&space;f(f(x+y).f(x-y))=xf(x)-y^2) on tenant compte de l'équation initiale,on trouve que : -y^2=x^2-yf(y)) on prenant x=y,il nous vient : =2x^2\Rightarrow&space;x(f(x)-x)=0) d’où f(x)=x pour x différant de 0 et le cas de x=0 est facile à traité .
Dernière édition par boubou math le Ven 23 Mar 2012, 12:19, édité 2 fois | |
|   | | boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mer 21 Mar 2012, 22:04 Mer 21 Mar 2012, 22:04 | |
| Problème 12Déterminer tous les triplets (x,y,z) de rationnels strictement positifs tels que les trois nombres  soient tous entiers. J'ajouterai ce lemme qui va sans doute faciliter la tache: Lemme - Spoiler:
Considérons =x^{n}+a_{n-1}x^{n-1}+.....+a_{1}x_{1}+a_{0}) avec n entier naturel non nul et &space;:a_i\in&space;\mathbb{Z}) Prouver que si  est une racine de P alors forcement t est entier .
| |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 23 Mar 2012, 16:18 Ven 23 Mar 2012, 16:18 | |
| - boubou math a écrit:
- Problème 12
Déterminer tous les triplets (x,y,z) de rationnels strictement positifs tels que les trois nombres

soient tous entiers. C'est pour la troisième fois que j’essayerai de poster ma solution ici, espérant qu'elle soit juste: On peut aisément prouver qu'il existe des entiers naturels a, b, et c et un entier d tel que  ,  et  . On a  est un entier, et donc  . On a  est un entier, et donc  . On a =d.\frac{ab+bc+ca}{abc}) est un entier, et donc  . Il résulte qu'on a  ,  et  .==>(*) Ce qui implique que  ,  et  . Ainsi, on peut démontrer aisément que :d|(a+n)(b+n)(c+n)-n^3) . Et, en particulier, on a  ,  et  . On suppose que d a un diviseur premier noté p, alors on trouve immédiatement que  ,  et  . Soit  ,  et  . Il s'ensuit qu'il existe des entiers r, s et t tel que 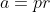 , 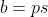 et 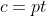 . La relation * déjà trouvée devient  ,  et  . Donc ) ,  et ) . Et puisque p est un diviseur premier de d, alors p est inférieur ou égal à d. On distingue donc deux cas: $Premier cas: p est strictement inférieur à d. La dernière relation s'écrit  ,  et  . (Sans oublier que r<a, s<b et t<c) Ainsi de suite, on pourrait créer une suite infinie et strictement décroissante d'entiers naturels vérifiant  ,  et  . Cela créerait alors une descente infinie d'entiers naturels, d'où la contradiction désirée. $Second cas: p=d. (i.e: d est premier) On a donc  ,  et  . Ce qui veut dire que x, y et z sont des entiers naturels. Maintenant, si x et y et z sont tous les trois strictement supérieurs à 3 on remarque que  est strictement inférieur à 1. Dans ce cas,  ne serait pas un entier. Ainsi, l'un des trois nombres x, y et z est inférieur ou égal à 3. Par symétrique des rôles, on suppose que z est inférieurs ou égal à trois. Et on doit analyser par conséquent 3 sous-cas: ---Si z=3, on doit chercher x et y tels que  soit un entier. Soit n un entier tel que  , c'est à dire que 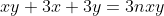 . Cette égalité impose que  . Et puisque 3 est premier, il s'ensuit qu'il divise l'un des facteur du produit: soit y par symétrique des rôles. Posons y=3m, l'égalité devient 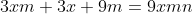 et ainsi 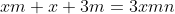 . On remarque que m divise x, ainsi x=hm où h est un entier naturel. On reprends dans l'égalité, il résulte que 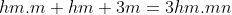 et ainsi 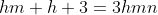 . On déduit que h divise 3 et donc h=3 ou h=1. -Si x=3m=y, l'équation de départ devient  ou bien 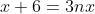 . On remarque que x divise 6, c'est à dire que x=6 ou x=3 ou x=2 ou x=1. Mais seul le cas x=3 (et donc y=3) qui marche. -Et si x=m (y=3x), l'équation de départ devient  ou bien 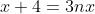 . On remarque que x divise 4, c'est à dire que x=4 ou x=2 ou x=1. Donc (x,y)=(4,12) ou (x,y)=(2,6) ou (x,y)=(1,3). Mais, le cas (x,y)=(2,6), seul, qui répond au problème. ---Si z=2, on doit chercher x et y tels que  soit un entier. La démarche suivie ressemble un peu à la précédente: Soit n un entier tel que  , c'est à dire que 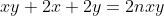 . L'un des nombre x et y doit être pair, soit y cet entier et posons y=2m. On aura 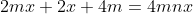 ou bien 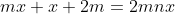 . On remarque que m divise x, et puis que x=2m ou bien x=m. -Si x=2m=y, l'équation de départ devient  et donc 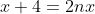 . On trouve donc que x est un des diviseurs de 4, donc x=4 ou x=2 ou x=1. On trouve que le cas x=4 (et donc y=4) est le seul qui marche. -Et si x=m (y=2x), l'équation de départ devient  ou bien 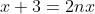 . On trouve donc que x divise 3, donc x=3 ou x=1. Donc (x,y)=(3,6) ou (x,y)=(1,2). Mais, le cas (x,y)=(3,6), seul, qui répond au problème. ---Si z=1, on doit chercher x et y tels que 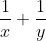 est un entier. Or, si  où n est un entier naturel, alors 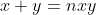 . Ce qui mène vers x divise y et y divise lui aussi x, ainsi x=y. On cherche donc x tel que  soit un entier. Donc x=1 et x=2 répondent au problème. ---Conclusion: Les triplets qui satisfont le problème sont (3,3,3); (2,3,6); (4,4,2); (1,1,1); (2,2,1) et leurs permutations. CQFD. Sauf erreurs. J'attends des jugement sur mon travail, ainsi qu'une solution alternative en usant du lemme proposé par boubou math.
Dernière édition par nmo le Sam 24 Mar 2012, 00:07, édité 1 fois | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 23 Mar 2012, 16:28 Ven 23 Mar 2012, 16:28 | |
| En attendant une confirmation de l'ensemble des solutions, je propose un nouvel exercice: Problème 13:Soient a, b et c des réels strictement positifs tel que  . Montrez que  . Bonne chance. | |
|   | | diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 23 Mar 2012, 19:12 Ven 23 Mar 2012, 19:12 | |
| - nmo a écrit:
C'est pour la troisième fois que j’essayerai de poster ma solution ici, espérant qu'elle soit juste:
On peut aisément prouver qu'il existe des entiers naturels a, b, et c et un entier d tel que  , ,  et et  . .
On a  est un entier, et donc est un entier, et donc  . .
On a  est un entier, et donc est un entier, et donc  . .
On a =d.\frac{ab+bc+ca}{abc}) est un entier, et donc est un entier, et donc  . .
Il résulte qu'on a  , ,  et et  .==>(*) .==>(*)
Ce qui implique que  , ,  et et  . .
Ainsi, on peut démontrer aisément que :d|(a+n)(b+n)(c+n)-n^3) . .
Et, en particulier, on a  , ,  et et  . .
On suppose que d a un diviseur premier noté p, alors on trouve immédiatement que  , ,  et et  . Soit . Soit  , ,  et et  . .
Il s'ensuit qu'il existe des entiers r, s et t tel que 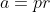 , , 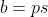 et et 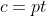 . .
La relation * déjà trouvée devient  , ,  et et  . .
Donc ) , ,  et et ) . .
Et puisque p est un diviseur premier de d, alors p est inférieur ou égal à d. On distingue donc deux cas:
$Premier cas: p est strictement inférieur à d.
La dernière relation s'écrit  , ,  et et  . (Sans oublier que r<a, s<b et t<c) . (Sans oublier que r<a, s<b et t<c)
Ainsi de suite, on pourrait créer une suite infinie et strictement décroissante d'entiers naturels vérifiant  , ,  et et  . .
Cela créerait alors une descente infinie d'entiers naturels, d'où la contradiction désirée.
$Second cas: p=d. (i.e: d est premier)
On a donc  , ,  et et  . .
Ce qui veut dire que x, y et z sont des entiers naturels.
. - boubou math a écrit:
- Problème 12
Déterminer tous les triplets (x,y,z) de rationnels strictement positifs tels que les trois nombres

soient tous entiers.
J'ajouterai ce lemme qui va sans doute faciliter la tache:
Lemme
- Spoiler:
Considérons =x^{n}+a_{n-1}x^{n-1}+.....+a_{1}x_{1}+a_{0}) avec n entier naturel non nul et &space;:a_i\in&space;\mathbb{Z}) Prouver que si  est une racine de P alors forcement t est entier .
Salut, Démonstration du lemme: avec (m,n)=1 On a m|a_0 et n|1 d'où t est forcement entier Considérons un polynome de 3 degrés et ses coefficients sont entiers et x,y,z ses solutions =ax^3+bx^2+cx+d) donc d'après viète x+y+z=-b/a, \sum xy= c/a et xyz=-d/a d'où a|b,c,d ,sans perte de généralité on peut supposer que a=1 donc x,y et z sont des entiers | |
|   | | boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 23 Mar 2012, 22:01 Ven 23 Mar 2012, 22:01 | |
| Excellente Solution Nmo, il fallait juste réessayer les solutions à la fin,tu trouveras que le triplet (1,1,2) n'est pas solution. je propose une autre solution se basant sur le lemme déjà cité : Preuve du Lemme :Soit  une racine du Polynôme P, avec p^q=1 et aussi q>0. On alors =\frac{p^n}{q^n}+a_{n-1}\frac{p^{n-1}}{q^{n-1}}+......+a_1\frac{p}{q}+a_0=0\Rightarrow&space;p^n=-q.a_{n-1}.p^{n-1}-....-q^{n-1}a_1.p-a_0.q^{n}\Rightarrow&space;p^n=-q(a_{n-1}.p^{n-1}+....+a_1.p.q^{n-2}+a_0.q^{n-1})) d’où  avec p^q=1 il nous vient q=1 implique t est entier . Revenons à l’exercice :Notons  tel que a,b et c sont des entiers naturels strictement positifs . On a ainsi =bc) donc d'après Viète x,y et z Sont les racine du polynôme =\alpha&space;^3-a\alpha&space;^2+bc\alpha&space;-c) En tenant compte du lemme x,y et z sont des entiers strictement positifs. Donc le problème se réduit à trouver tous les entiers strictement positifs tels que  Le reste de la preuve ne diffère pas trop de ce tu as déjà mentionné .
Dernière édition par boubou math le Sam 24 Mar 2012, 08:38, édité 1 fois | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Sam 24 Mar 2012, 00:16 Sam 24 Mar 2012, 00:16 | |
| - boubou math a écrit:
- Excellente Solution Nmo, il fallait juste réessayer les solutions à la fin,tu trouveras que le triplet (1,1,2) n'est pas solution.
Bien vu, c'est édité... - Spoiler:
Pour les curieux, essayez de faire le problème quivant: Déterminez trois entiers m, n et p tel que le produit (\frac{1}{m}+\frac{1}{n}+\frac{1}{p})) soit un entier. Bonne chance.
| |
|   | | momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Sam 24 Mar 2012, 15:45 Sam 24 Mar 2012, 15:45 | |
| - nmo a écrit:
- Spoiler:
Pour les curieux, essayez de faire le problème quivant: Déterminez trois entiers m, n et p tel que le produit (\frac{1}{m}+\frac{1}{n}+\frac{1}{p})) soit un entier. Bonne chance.
Je choisis les entiers 1, 1 et 1 
Dernière édition par momo1729 le Sam 24 Mar 2012, 15:48, édité 1 fois | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Sam 24 Mar 2012, 16:07 Sam 24 Mar 2012, 16:07 | |
| - momo1729 a écrit:
- nmo a écrit:
- Spoiler:
Pour les curieux, essayez de faire le problème quivant: Déterminez trois entiers m, n et p tel que le produit (\frac{1}{m}+\frac{1}{n}+\frac{1}{p})) soit un entier. Bonne chance.
Je choisis les entiers 1, 1 et 1  Si tu es curieux, essaie de trouver tous les couples qui vérifie ce que j'ai dit. De plus, cet exercice n'est pas l'exercice courant. On peut discuter par messagerie privée. | |
|   | | momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 25 Mar 2012, 08:50 Dim 25 Mar 2012, 08:50 | |
| - nmo a écrit:
- En attendant une confirmation de l'ensemble des solutions, je propose un nouvel exercice:
Problème 13:
Soient a, b et c des réels strictement positifs tel que  . .
Montrez que  . .
Bonne chance. Je propose cette solution qui n'est pas la mienne. Posons  , etc. ainsi on a  et il nous faut :  Soit  , etc. Remarquons que :  d’où le résultat.
Dernière édition par momo1729 le Dim 25 Mar 2012, 08:53, édité 1 fois | |
|   | | momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 25 Mar 2012, 08:52 Dim 25 Mar 2012, 08:52 | |
| Problème 14Trouver toutes les fonctions de l'ensemble des réels strictement positifs vers lui-même satisfaisant pour tous  :  | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 25 Mar 2012, 23:12 Dim 25 Mar 2012, 23:12 | |
| bonsoir : on pose ,P(x,y) l'assertion : f(x)f(yf(x))=f(x+y) . 1) si f est constante alors f(x)=1 quelque soit x >0 . Maintenant ,si f est non constante , alors existe un ''a'' >0 , tel que: f(a) >1 . P(a, a\f(a)-1) , on obtient : f(a)=1 impossible , ainsi f(x)=<1 quelque soit x >0 , d'ou f est décroissante ( f(x) >=f(x+y)) ,D'ou il existe un c >0 tel que : quelque soit x >0 dans l'intervalle ]0,c[ f(x)=1 et quelque soit x dans l'intervalle ]c ,+infini[ f(x) < 1 , P(2c\3,2c\3) entraîne a 1<1contradiction . On en déduit que : 0<f(x)<1 quelque soit x > 0 d'ou : f(x+y) < f(x) ainsi f est strictement décroissante (car: x+y >x quelque soit x,y>0 ) , en particulier f est injective . ainsi P(x,y): f(x)f(yf(x))=f(x+y)=f(yf(x)+(x+y-yf(x)))=f(yf(x)) .f(f(yf(x))(x+y-yf(x)) (x+y(1-f(x))>0) il s'ensuit que : x=f(yf(x))(x+y-yf(x)) quelque soit x,y > 0 (par l'injectivité de f) . en prenant x=1 et y=t\f(1) . on obtient : f(t)=1\(1+ut) quelque soit t >0 avec u=1\f(1)-1 . réciproquement les solutions de l'équation sont de type f(x)=1\(cx+1) avec c >=0 .
Dernière édition par Oty le Lun 02 Avr 2012, 01:00, édité 7 fois | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 25 Mar 2012, 23:58 Dim 25 Mar 2012, 23:58 | |
| Problème 15 : Dans un triangle ABC ,on choisit trois points D , E et F appartenant aux segments BC , AC , AB respectivement , de tel manière que : AF=BD=CE et l' angle BDF=CED=AFE .Montrer que ABC est équilatéral . | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Sam 31 Mar 2012, 21:29 Sam 31 Mar 2012, 21:29 | |
| Bonsoir , voici ma démonstration pour le problème 15 : il est facile de prouver que les triangles  et  sont semblable , ce qui nous permet d'établir ces trois égalités : 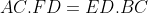 (1) , 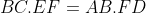 (2) , 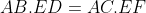 . On pose :  ,  et  . Maintenant on va essayé d'exprimé les ces trois égalités en fonction des longueurs des cotés du triangles ainsi que ses angles et ses paramètres fixe ; avec la loi des sinus dans les trois petits triangles on parvient a établir c'est nouvelle égalité : }{sin(x))}.BF=\frac{sin(\widehat{B})}{sin(x)}.(c-y)) , }{sin(x)}.(a-y)) et }{sin(x)}.(b-y)) . On remplace dans les 3) égalité établie au préliminaire , notant que : ( =b.sin(C)&space;,&space;a.sin(C)=c.sin(A)&space;,&space;b.sin(A)=a.sin(B)) ,loi des sinus ) qui vont nous permettre de faire des simplification , on sommant j'ai obtenue cette jolie égalité : -y(a+b+c)=(a^2+b^2+c^2)-y(a.\frac{sin(A)}{sin(B)}+b.\frac{sin(B)}{sin(C)}+c.\frac{sin(C)}{sin(A)})) ; mais avec la loi des sinus encore , on remplace les rapport entre les sinus par les rapport entre les longueurs des cotés , après simplification on obtient finalement cette surprenante égalité :  , qui est équivalente a : ^2}{b}+\frac{(b-c)^2}{c}+\frac{(c-a)^2}{a}=0) , d'ou le résultat , sauf erreur ...
Dernière édition par Oty le Mar 01 Mai 2012, 17:07, édité 1 fois | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Sam 31 Mar 2012, 22:21 Sam 31 Mar 2012, 22:21 | |
| Problème 16 : Résoudre dans N² l'équation :  . Bonne chance  . | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  | |
| |
|   | | | | Le dernier jeu pour la préparation aux IMOs 2012: |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
