| | Le dernier jeu pour la préparation aux IMOs 2012: |  |
|
+14alidos Ahmed Taha (bis) Maths_BT amigo-6 darkpseudo Coulomb yasserito momo1729 boubou math Mehdi.O az360 diablo902 Oty nmo 18 participants |
|
| Auteur | Message |
|---|
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 04 Mai 2012, 20:35 Ven 04 Mai 2012, 20:35 | |
| Moi aussi je n'ai pas bien compris cette partie-là. Ni comment il peut "facilement" prouver que 2^201=-1(mod 2011). On pourrait lui demander... mais la solution qui utilise le symbole de Legendre est superbe, tu ne trouves pas ? (c'est aussi la solution officielle qu'ils donnent sur le polycopié d'Animath).
Dernière édition par momo1729 le Ven 04 Mai 2012, 20:40, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 04 Mai 2012, 20:39 Ven 04 Mai 2012, 20:39 | |
| - momo1729 a écrit:
- Moi aussi je n'ai pas bien compris cette partie-là. Ni comment il peut "facilement" prouver que 2^201=1(mod 2011). On pourrait lui demander... mais la solution qui utilise le symbole de Legendre est superbe, tu ne trouves pas ? (c'est aussi la solution officielle qu'ils donnent sur le polycopié d'Animath).
C'est pour cela que j'avais l'impression de l'avoir vu quelque part! Moi aussi, j'ai apprécié la seconde solution... Et voici le problème courant: - darkpseudo a écrit:
- Exo :
Plus facile , sois ABC un triangle A' et B' les milieux de [BC] et [AC] , M le point d'intersection de (AA') et (BB') ; A'MB'C est CIRCONSCRIPTIBLE , montrez que ABC est isocèle . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 06 Mai 2012, 10:21 Dim 06 Mai 2012, 10:21 | |
| - darkpseudo a écrit:
- Exo :
Plus facile , sois ABC un triangle A' et B' les milieux de [BC] et [AC] , M le point d'intersection de (AA') et (BB') ; A'MB'C est CIRCONSCRIPTIBLE , montrez que ABC est isocèle . Je propose une solution à ce problème: On pose premièrement AC=b, BC=a et AB=c. Puisque M est l'intersection des deux médianes (AA') et (BB'), alors M est le centre de gravité du triangle ABC. On a  et  . De plus, on a  et  . Et puisque MB'CA' est circonscriptible, il vient que  . Et ainsi  .==>(1) Or, on a selon le théorème de la médiane: -a^2}) et -b^2}) . La relation 1 devient -a^2}+3b=\sqrt{2(a^2+c^2)-b^2}+3a) donc -a^2}-\sqrt{2(a^2+c^2)-b^2}=3a-3b) . Et ainsi -a^2-2(a^2+c^2)+b^2}{\sqrt{2(b^2+c^2)-a^2}+\sqrt{2(a^2+c^2)-b^2}}=3a-3b) ou encore (b+a)}{\sqrt{2(b^2+c^2)-a^2}+\sqrt{2(a^2+c^2)-b^2}}=-(b-a)) . La dernière relation équivaut à 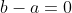 car -a^2}+\sqrt{2(a^2+c^2)-b^2}}\neq-1) . Et finalement 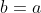 . Ce qui veut dire que ABC est un triangle isocèle. CQFD. Sauf erreurs. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 06 Mai 2012, 10:30 Dim 06 Mai 2012, 10:30 | |
| Je propose un nouveau problème: Problème 28:Trouvez toutes les fonctions f continues et strictement monotone qui satisfont =1) et :f(f(x))=(f(x))^2) . Bonne chance. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 | |
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Lun 07 Mai 2012, 18:58 Lun 07 Mai 2012, 18:58 | |
| Je pense que le théorème de bijection n est pas suffisant pour dire que la fonction admet f:x->x² comme solution
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Lun 07 Mai 2012, 20:38 Lun 07 Mai 2012, 20:38 | |
| - Mehdi.O a écrit:
- nmo a écrit:
- Je propose un nouveau problème:
Problème 28:
Trouvez toutes les fonctions f continues et strictement monotone qui satisfont =1) et et :f(f(x))=(f(x))^2) . .
Bonne chance. D'après le théorème de bijection, f est bijective et donc surjective, ainsi f:x|->x², mais celle-ci n'est pas strictement monotone, donc aucune fonction ne vérifie l'EF. Essaie avec la fonction f définie par: :f(x)=\begin{cases}1\;\;;1\le x\\x^2;0\le x\le1\\0\;\;;x\le0\end{cases}) . Au plaisir! | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mer 09 Mai 2012, 16:37 Mer 09 Mai 2012, 16:37 | |
| La fonction que tu donnes n'est pas strictement monotone... | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mer 09 Mai 2012, 16:59 Mer 09 Mai 2012, 16:59 | |
| - darkpseudo a écrit:
- Indice
- Spoiler:
Considérer le polynôme sum a_(i)*X^(i)
Pourrais-tu clarifier pourquoi les racines p-ième de l'unité sont racine de ce polynôme ? Merci | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mer 09 Mai 2012, 18:32 Mer 09 Mai 2012, 18:32 | |
| Car par exemple pour j la racine troisième , tu vas les rassembler de la manière suivante :
sum a_i ( i=0 mod 3 ) * 1 + sum a_i ( i=1mod 3 ) *j + sum a _i (i=2mod3 ) * j^(2) et vu que ces tois sommes sont les mêmes ( hypothèse de l'énoncé ) tu auras (1+j+j^(2))*(sum a_i (i=0mod 3 )) = 0 car 1+j+j^(2)=0 | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Jeu 10 Mai 2012, 12:31 Jeu 10 Mai 2012, 12:31 | |
| Désolé pour cette question dont je viens de m'apercevoir qu'elle est stupide...
@ amigo :
f est surjective, donc tout y dans R admet un antécédent x par f. On a donc : f(y)=f(f(x))=f(x)^2=y^2 . Et comme on a pris y quelconque, on voit bien que f est la fonction x|-> x^2. | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Jeu 10 Mai 2012, 12:41 Jeu 10 Mai 2012, 12:41 | |
| J ai eu l idée en premier mais je croyais que l ex est plus difficile que ca! | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Lun 14 Mai 2012, 01:04 Lun 14 Mai 2012, 01:04 | |
| si personne n'y voit d'inconvénient je propose un peu de combinatoire assez intéressante . Problème 29 : De combien de façon on peut représenté le nombre 27 comme somme de : a1+a2+...+a6 avec 0=<ai=<9 (et ai dans N ) . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Sam 16 Juin 2012, 01:02 Sam 16 Juin 2012, 01:02 | |
| il est temps de ranimer ce sujet maintenant que le bac est passé  , le probleme 29 : est encore sans solution . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 19 Juin 2012, 00:17 Mar 19 Juin 2012, 00:17 | |
| - Oty a écrit:
- si personne n'y voit d'inconvénient je propose un peu de combinatoire assez intéressante . Problème 29 : De combien de façon on peut représenté le nombre 27 comme somme de : a1+a2+...+a6 avec 0=<ai=<9 (et ai dans N ) .
- Oty a écrit:
- il est temps de ranimer ce sujet maintenant que le bac est passé
 , le probleme 29 : est encore sans solution . , le probleme 29 : est encore sans solution . Je pense que ce problème est d'une difficulté monstrueuse de telle sorte que personne n'a pu proposer une solution. Merci d'en proposer une, pour qu'on puisse continuer! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 | |
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 | |
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 19 Juin 2012, 16:32 Mar 19 Juin 2012, 16:32 | |
| Nouveau Problème : trouver tous les entiers solution de l’équation : ) | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 19 Juin 2012, 18:59 Mar 19 Juin 2012, 18:59 | |
| ... 
Dernière édition par yasserito le Mar 19 Juin 2012, 23:13, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 19 Juin 2012, 19:14 Mar 19 Juin 2012, 19:14 | |
| - yasserito a écrit:
- Premiérement,il est facile de demontrer que 1997 est un nombre premier.
on remarque d'abord que (0,0) est solution a l'équation .
Soit maintenant (x,y) solution a l'équation tel que (x,y)=/=(0,0) alors x²+y²=/=0
Supposons que x²+y²=1997 ,alors x-y=1 ainsi y²+y=998 impossible
Alors on a (x²+y²)^1997=1
Alors selon Gauss on obtient x²+y²/(x-y)
Et puisque x²+y²>lx-yl car (x-1/2)²+(y+1/2)²>1/2 et (x+1/2)²+(y-1/2)²>1/2
Alors x-y=0 alors x²+y²=0.contradiction
Alors le seul couple solution a l'equation est (0,0).
Sauf erreur. Tu as tort! Ce n'est pas le seul couple de solution. Essaye le couple: (1997,-1997). Il marche sûrement! Je présenterai ma méthode dans quelque instant!
Dernière édition par nmo le Mar 19 Juin 2012, 19:21, édité 1 fois | |
|
  | |
Maths_BT
Habitué
 Nombre de messages : 19 Nombre de messages : 19
Age : 28
Localisation : Meknès
Date d'inscription : 08/06/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 19 Juin 2012, 19:19 Mar 19 Juin 2012, 19:19 | |
| (0.0) tout à fait juste  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 19 Juin 2012, 19:22 Mar 19 Juin 2012, 19:22 | |
| - Maths_BT a écrit:
- (0.0) tout à fait juste
 Certes, mais il se peut que l'équation admet d'autres solutions! | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 19 Juin 2012, 20:47 Mar 19 Juin 2012, 20:47 | |
| - nmo a écrit:
- Maths_BT a écrit:
- (0.0) tout à fait juste
 Certes, mais il se peut que l'équation admet d'autres solutions! il y a 12 couples je pense | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 19 Juin 2012, 22:21 Mar 19 Juin 2012, 22:21 | |
| Je me permet de faire une résolution partielle:
On remarque que 1997^(2)-4y(y+1997) doit être un carré parfait ( condition sur le discriminant de l'equation du second degré en x).
or on a 1997^(2)+4y(y+1997)=(1997+2y)^(2) .
Notons le premier carré a^(2) et le second b^(2) connaître a et b permet de résoudre le problème on a alors :
a^(2)+b^(2)=2*1997^(2) => ((a+b)/2)^(2)+((a-b)/2)^(2)=1997^(2) ceçi est un triplet pythagoricien chaque couple d'entiers donc la somme des carré donne 1997 permet alors d'avoir une solution. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 19 Juin 2012, 22:39 Mar 19 Juin 2012, 22:39 | |
| - Oty a écrit:
- Nouveau Problème : trouver tous les entiers solution de l’équation :
) Voici ma solution: On écrit l'équation sous la forme =0) . Il s'agit donc d'une équation du second degré dont l'inconnue est y. Le discriminent de cette équation est bel et bien ) . Et pour que les solutions de l'équation de départ soient des entiers, il faut et il suffit que ce discriminent soit un carré parfait! Ainsi, il existe un entier t tel qu'on ait  ou encore  .==>(*) L'égalité s'écrit une nouvelle fois =0) . Encore une fois, on doit calculer le discriminent =16(2\times1997^2-t^2)) . Et pour que x soit un entier, il faut et il suffit encore une fois que  soit un carré parfait. Ainsi, il existe un entier s tel qu'on ait  ou bien  . Ainsi, on s'intéresse à la décomposition de l'entier  en deux carrés. On est sûr selon le théorème de deux carrés de Fermat que le nombre de décomposition différente de cet entiers en deux carré est 2. Une qui saute aux yeux, c'est  . Et l'autre c'est  après la recherche. Du fait, on a trois cas =(1997^2,1997^2)) , =(1657^2,2287^2)) ou =(2287^2,1657^2)) . Maintenant, on cherche les valeurs possibles de x. ***Le premier cas: =(1997^2,1997^2)) . On a donc  et  . Ainsi  ou encore =0) . Ce qui donne deux cas: 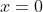 ou 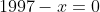 . _Si 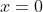 . En reportant dans l'équation initiale, on aura  . Donc  , soit =0) . Ainsi 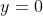 ou 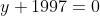 . Et finalement 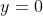 ou 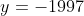 . On tire ainsi les deux solutions (0,0) et (0,-1997). _Si 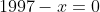 , c'est à dire que 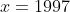 . En reportant dans l'équation initiale, on aura =1997^2-1997y) . Donc  . D'où 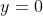 ou 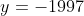 . On tire ainsi deux autres solutions (1997,0) et (1997,-1997). ***Le second cas: =(1657^2,2287^2)) . On a donc  et  . Et notre équation devient  . En réduisant par 4, cela équivaut à  . Et on a  et 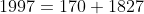 . Donc la dernière équation équivaut à 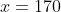 ou 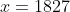 . _Si 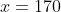 . En reportant dans l'équation initiale, on aura ) . Donc  , soit  Et on a \times145) et +145) . l'équation dans ce cas équivaut à 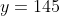 ou 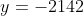 . On tire ainsi deux autres solutions (170,145) et (170,-2142). _Si 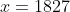 . En reportant dans l'équation initiale, on aura ) . Donc  , soit  . Et comme précédemment, on tombe sur 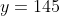 ou 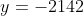 . Ce qui donne encore deux solutions (1827,145) et (1827,-2142). ***Le troisième cas: =(2287^2,1657^2)) . On a donc  et  . Et notre équation devient  . En réduisant par 4, cela équivaut à  . Et on a \times2142) et +2142) . Donc la dernière équation équivaut à 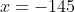 ou 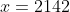 . _Si 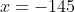 . En reportant dans l'équation initiale, on aura ^2+y^2=1997(-145-y)) . Donc  , soit  . Et on a \times(-1827)) et +(-1827)) . l'équation dans ce cas équivaut à 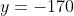 ou 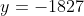 . Et on tire les deux solutions (-145,-170) et (-145,-1827). _Si 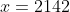 . En reportant dans l'équation initiale, on aura ) . Donc  , soit  . Et comme précédemment, on tombe sur 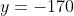 ou 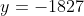 . Ce qui donne encore deux solutions (2142,-170) et (2142,-1827). ***Conclusion: Si S est l'ensemble des solutions de l'équation proposée, alors on doit avoir: ;(-145,-170);(0,-1997);(0,0);(170,-2142);(170,145);(1827,-2142);(1827,145);(1997,-1997);(1997,0);(2142,-1827);(2142,-170)\}) Et ce sont 12 couples de solutions. Ce qui clôt cette démonstration pénible.
Dernière édition par nmo le Mer 20 Juin 2012, 00:20, édité 4 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  | |
| |
|
  | |
| | Le dernier jeu pour la préparation aux IMOs 2012: |  |
|
