| | Le dernier jeu pour la préparation aux IMOs 2012: |  |
|
+14alidos Ahmed Taha (bis) Maths_BT amigo-6 darkpseudo Coulomb yasserito momo1729 boubou math Mehdi.O az360 diablo902 Oty nmo 18 participants |
|
| Auteur | Message |
|---|
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 01 Avr 2012, 10:54 Dim 01 Avr 2012, 10:54 | |
| ... 
Dernière édition par yasserito le Dim 01 Avr 2012, 15:54, édité 1 fois | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 01 Avr 2012, 11:40 Dim 01 Avr 2012, 11:40 | |
| Solution au problème 16:Déjà on peut remarquer que x=0[3] ou x=2[3] Si x=0[3]: on a y²=(x^4+x)/3=(x+1)(x²-x+1)(x/3) avec (x+1)^(x²-x+1)=(x²-x+1)^(x/3)=(x+1)^(x/3)=1 Alors il existe (a,b,c)£IN.IN*.IN* tel que x=3a² et x+1=b² et x²-x+1=c² Alors (c-2b²+3)(c+2b²-3)=3 ainsi on trouve que c=2 et b=1 =>x=0 Si x=2[3]: on a y²=(x^4+x)/3=x(x²-x+1)((x+1)/3) Alors il existe (a,b,c)£(IN*)^3 tel que x=a² et x+1=3b² et x²-x+1=c² Ainsi on trouve qu'il n'existe pas de solutions tel que x=2[3] Alors la seule solution de cette équation est le couple (0,0). - Spoiler:
J'ai pas de problèmes à proposer.
Dernière édition par yasserito le Dim 01 Avr 2012, 11:54, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 01 Avr 2012, 11:45 Dim 01 Avr 2012, 11:45 | |
| - Oty a écrit:
- Problème 16 : Résoudre dans N² l'équation :
 . Bonne chance . Bonne chance  . . Je propose ma solution: On remarque d'emblée qu'on a ou bien ) ou bien ) , car l'équation s'écrit (x^2-x+1)) . On doit donc traiter chaque cas séparément: Le premier cas: ) . Alors, il existerait un entier k tel que 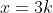 . L'équation initiale devient alors (9k^2-3k+1)) . On peut facilement démontrer que les trois nombres  , 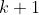 et  sont premier entre eux soit dans leurs ensemble, soit deux à deux. Ainsi, la dernière équation implique qu'ils sont tous des carrés. D'où l’existence d'un entier c tel que  .==>(1) Et donc  , ce qui est une équation du second degré d'inconnue k et de paramètre c. Le discriminent de cette équation est le nombre ^2-4\times9\times(1-c^2)=9(1-4+4c^2)=9(4c^2-3)) . Et pour que l'équation admet des solutions entières, il faut que  soit un carré parfait, i.e ^2-3) soit un carré parfait. On doit chercher donc un entier t tel que ^2-3=t^2) , ce qui s'écrit encore (2c+t)=3) . Cette égalité impose que 2c+t=3 et 2c-t=1 (l'autre cas n'est pas valide dans l'ensemble des entiers). Et par conséquent c=1 et t=1. En reprenant dans 1, on tombe sur =0) . Ce qui implique que k=0. Donc x=0. Ainsi le couple (0,0) est solution au problème. Le deuxième cas: ) . On procède presque de la même manière que précédemment: Il existe un entier k tel que 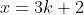 . L'équation initiale devient (k+1)(9k^2+4+12k-3k-2+1)) . Soit encore (3k+2)(3k^2+3k+1)) . Cela veut dire que 3 divise 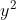 , donc 3 divise y. Il existe donc un entier m tel que y=3m. Par conséquent (3k+2)(3k^2+3k+1)) . Et cela implique que k+1 est forcément multiple de 3. Il existe donc un entier n tel que k=3n+2. On écrit ainsi (9n+<img src=) (27n^2+45n+19)" border="0" alt=""/>. De plus il est facile de voir que les nombres 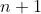 ,  et  sont premiers entre eux dans leurs ensemble, voire deux à deux. Ils sont donc tous des carrés parfait. Donc il existe deux entiers a et b tel que  et  . Cela impliquerait que  . Donc (3a+b)=1) . Cela doit donner 3a+b=1 et 3a-b=1, donc 6a=2 ou encore 3a=1, ce qui est absurde. Et donc, il n'existe pas de solution dans ce cas. Synthèse:L'équation proposée admet une solution unique, qui est la couple (0,0). Sauf erreur. EDIT: il parait que yasserito m'a devancé, donc c'est à lui de proposer un nouveau problème. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 01 Avr 2012, 13:22 Dim 01 Avr 2012, 13:22 | |
| Bravo a vous deux , a toi de proposé nmo , vu que yasserito laisse le champ libre . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 01 Avr 2012, 13:32 Dim 01 Avr 2012, 13:32 | |
| - Oty a écrit:
- Bravo a vous deux , a toi de proposé nmo , vu que yasserito laisse le champ libre .
Bon, mon problème est de la géométrie: Problème 17:Sur un demi cercle de rayon 1, on considère quatre cordes AB, BC, CD et DE de longueurs respectifs a, b, c et d de façon que les arcs de cercles correspondant n'aient pas de points communs autres que leurs extrémités. Démontrez que  . Bonne chance. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Lun 02 Avr 2012, 22:44 Lun 02 Avr 2012, 22:44 | |
| proposition pour le Problème : 17 , on pose S le membres de droite de l"inégalité , on remarque que S est maximal si l'un des segments formé par ces 5 points est un diamètre de ce semi-cercle , supposant que c'est AE, alors AE=2 , et on a l'angles ACE=90° . posant : AC=x et CE=y (ses deux longueur dépende , de a,b,c,d ) par Pythagore on a : 4=x²+y²(*) , dans le quadrilatère ACDE (inscriptible ) on a : 2c+dx=EC.AD (On exprime AD en fonction de 4 et d , puis CE en fonction de 4 et x , tjrs a l'aide de Pythagore) en élevant au carré cette égalité se transforme en : c²+d²+x²+xcd=4 (1) , par un raisonnement analogue on trouve de même que : a²+b²+y²+aby=4 (2) . en sommant (1) et (2) et en prenant compte de (*) on a : 8=a²+b²+c²+d²+cdx +aby+4 donc : a²+b²+c²+d²+cdx+aby=4 , ainsi 4>S équivalant a : aby+cdx > abc +bcd (**), mais puisque : l'angle ABD=ABE+EBC=90+EBC > 90 , il s'ensuit d’après Al-kashi que : AC=x>b , de même que y>c , par conséquent l"inégalité (**) est vrai .... | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 03 Avr 2012, 22:04 Mar 03 Avr 2012, 22:04 | |
| Problème 18 : soit un entier naturel : n >= 2 , et des réels  , tel que :  . Trouver la valeur maximal de : .(\sum_{i=1}^n\frac{a_{i}}{i})^2) . | |
|
  | |
Coulomb
Débutant

 Nombre de messages : 9 Nombre de messages : 9
Age : 30
Date d'inscription : 31/01/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Sam 07 Avr 2012, 18:19 Sam 07 Avr 2012, 18:19 | |
| probléme 19 :lim quand x tend vers 0 de ( ( tanx - x )/(sinx - x ) ) je crois c'est facile  bn chance | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Sam 07 Avr 2012, 20:18 Sam 07 Avr 2012, 20:18 | |
| Bonsoir a coulomb , veille a respecté les règles du jeu ! tu dois d’abords , au moins avoir résolue le problème 18 pour pouvoir proposé un nouveau , de plus je ne pense pas que ton problème soit un olympiade . | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 10 Avr 2012, 16:38 Mar 10 Avr 2012, 16:38 | |
| @Oty : Animath  | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Mar 10 Avr 2012, 16:45 Mar 10 Avr 2012, 16:45 | |
| oui Momo1729 , poste la solution si tu veux , pour continuer le jeu  . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 13 Avr 2012, 12:22 Ven 13 Avr 2012, 12:22 | |
| - Coulomb a écrit:
- probléme 19 :
lim quand x tend vers 0 de ( ( tanx - x )/(sinx - x ) )
je crois c'est facile  bn chance bn chance Même s'il n'est pas un exercice d'olympiade, je te propose de jeter un coup d'oeuil ici: https://mathsmaroc.jeun.fr/t18510-difficile#158441. A la prochaine fois, veille à respecter les règles du jeu. - Oty a écrit:
- Problème 18 : soit un entier naturel : n >= 2 , et des réels
 , tel que : , tel que :  . Trouver la valeur maximal de : . Trouver la valeur maximal de : .(\sum_{i=1}^n\frac{a_{i}}{i})^2) . . - Oty a écrit:
- oui Momo1729 , poste la solution si tu veux , pour continuer le jeu
 . . Comme momo1729 ne veut plus proposer la solution, je fais ce copier-coller:  . P.S: je ne savais pas que c'était un exercice des olympiades françaises, et az_360 m'a proposé une solution pareille durant le dernier stage. Je vais chercher un exercice afin de revivre le jeu. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Ven 13 Avr 2012, 12:39 Ven 13 Avr 2012, 12:39 | |
| Voici un problème que je n'ai pas encore traité: Problème 20:Trouvez toutes les fonctions définies sur l'ensemble des entiers naturels non nuls, et qui satisfont: \in\mathbb{N}^2):f(f(m)^2+2f(n)^2)=m^2+2n^2) . Bonne chance. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 15 Avr 2012, 21:04 Dim 15 Avr 2012, 21:04 | |
| je propose une solution au probléme 20 , histoire de ne pas tuer le jeu . il est clair que f est injective , Remarquant que , ^2+2x^2=(x-1)^2+2(x+2)^2) , on remplace dans l'EF , il s'ensuit avec l'injectivité de f que : ^2+2f(x)^2=f(x-1)^2+2f(x+2)^2) , considérant mnt une suite ^2) , d'apres la relation qu'on a obtenu il vient que :  , pour n >1 , la solution de cette relation linéaire est : ^n) , avec a,b,c,d des constante . De l'equation initial on a :  d'ou b=0 , ainsi : ^n) , qui est le carré d'un entier naturel que si : c=d=0 et a un carré parfait : ainsi f(n)=kn pour tout n >0 , réciproquement seul f(n)=n pour tout n >0 vérifie l EF .
Dernière édition par Oty le Mer 22 Aoû 2012, 20:22, édité 1 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 15 Avr 2012, 21:22 Dim 15 Avr 2012, 21:22 | |
| Problème 21: On considère deux entier m et n , tels que m>1 et n>1 avec m pair . soit une fonction f définie dans R* et vérifiant les conditions suivantes :1)- =\frac{f(x_{1})^m+...+f(x_{n})^m}{n}&space;,\forall{x_{1},x_{2},...,x_{n}\in{\mathbb{R}^*}}) , 2)- \neq{2004}) et \neq{0}) . Calculez ) . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Sam 21 Avr 2012, 22:11 Sam 21 Avr 2012, 22:11 | |
| - Oty a écrit:
- Problème 21: On considère deux entier m et n , tels que m>1 et n>1 avec m pair . soit une fonction f définie dans R* et vérifiant les conditions suivantes :1)-
=\frac{f(x_{1})^m+...+f(x_{n})^m}{n}&space;,\forall{x_{1},x_{2},...,x_{n}\in{\mathbb{R}^*}}) , , 2)- \neq{2004}) et \neq{0}) ) . . Je vais essayer de donner une solution à ce problème: La source du problème dit que f est définie sur 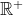 . (Voir le sixième test des olympiades marocaines de l’année scolaire 2005-2006) Alors, je propose ma démonstration dans ce cas (0 est inclus), sinon je me suis bloqué parfaitement. Premièrement, on pose  : x_i=a) alors l'équation fonctionnelle implique que :f(a^m)=f(a)^m) . Notre équation fonctionnelle se réécrit donc \in({\mathbb{R}^+})^n}):f(\frac{x_{1}^m+\cdots+x_{n}^m}{n})=\frac{f(x_1^m)+\cdots+f(x_n^m)}{n}) . On pose maintenant:  : x_i^m=\alpha_i) . On aura donc \in{(\mathbb{R}^+)^n}}):f(\frac{\alpha_{1}+\cdots+\alpha_{n}}{n})=\frac{f(\alpha_1)+\cdots+f(\alpha_n)}{n}) . On prend maintenant n=2, on aura \in{(\mathbb{R}^+)^2}}):f\bigg(\frac{x+y}{2}\bigg)=\frac{f(x)+f(y)}{2}) . On reconnait ainsi l'équation fonctionnelle de Jensen, dont les solutions sont les fonctions affines sur l'ensemble des nombres rationnels. On se contente aux entiers, et on écrit: :f(x)=kx+c) où \in{(\mathbb{R}^+)^2}}) . Maintenant, si on prend  : x_i=0) on doit avoir =f(0)^m) et donc =0) ou =1) . De même, on tombe sur =0) ou =1) . On discute maintenant les quatre cas possibles: *Le premier cas: =f(0)=0) . On aura directement  , et par conséquent f est intégralement nulle. Ce qui vient en contradiction avec le fait que \neq{0}) . *Le second cas: =1) et =0) . Tout de suite, on aura 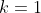 et 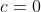 , et par conséquent :f(x)=x) . Ce qui vient en contradiction avec le fait que \neq{2004}) . *Le troisième cas: =0) et =1) . On aura donc 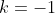 et 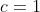 , et il s'ensuit que :f(x)=-x+1) . Dans ce cas, f n'est pas définie sur 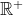 . (Le côté gauche de l'équation fonctionnelle de départ est positif, le côté droit doit l'être ainsi. Ainsi f est à valeurs dans l'ensemble des réels positifs) *Le quatrième cas: =f(0)=1) . On aura donc 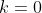 et 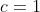 , et il s'ensuit que :f(x)=1) . Dans ce cas, =1) . D'où la conclusion. Sauf erreurs. P.S:J'ai souffert avec ce problème, et je serai reconnaissant si quelqu'un indique s'il y avait des fautes. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 22 Avr 2012, 10:25 Dim 22 Avr 2012, 10:25 | |
| En attendant une confirmation, je propose un nouveau problème: Problème 22:Déterminez tous les entiers n satisfaisant ^n\bigg)) . (E étant la fonction partie entière.) Bonne chance. | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 22 Avr 2012, 12:03 Dim 22 Avr 2012, 12:03 | |
| - nmo a écrit:
- Oty a écrit:
- Problème 21: On considère deux entier m et n , tels que m>1 et n>1 avec m pair . soit une fonction f définie dans R* et vérifiant les conditions suivantes :1)-
=\frac{f(x_{1})^m+...+f(x_{n})^m}{n}&space;,\forall{x_{1},x_{2},...,x_{n}\in{\mathbb{R}^*}}) , , 2)- \neq{2004}) et \neq{0}) ) . . Je vais essayer de donner une solution à ce problème:
La source du problème dit que f est définie sur 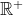 . .
(Voir le sixième test des olympiades marocaines de l’année scolaire 2005-2006)
Alors, je propose ma démonstration dans ce cas (0 est inclus), sinon je me suis bloqué parfaitement.
Premièrement, on pose  : x_i=a) alors l'équation fonctionnelle implique que alors l'équation fonctionnelle implique que :f(a^m)=f(a)^m) . .
Notre équation fonctionnelle se réécrit donc \in({\mathbb{R}^+})^n}):f(\frac{x_{1}^m+\cdots+x_{n}^m}{n})=\frac{f(x_1^m)+\cdots+f(x_n^m)}{n}) . .
On pose maintenant:  : x_i^m=\alpha_i) . .
On aura donc \in{(\mathbb{R}^+)^n}}):f(\frac{\alpha_{1}+\cdots+\alpha_{n}}{n})=\frac{f(\alpha_1)+\cdots+f(\alpha_n)}{n}) . .
On prend maintenant n=2, on aura \in{(\mathbb{R}^+)^2}}):f\bigg(\frac{x+y}{2}\bigg)=\frac{f(x)+f(y)}{2}) . .
On reconnait ainsi l'équation fonctionnelle de Jensen, dont les solutions sont les fonctions affines sur l'ensemble des nombres rationnels.
On se contente aux entiers, et on écrit: :f(x)=kx+c) où où \in{(\mathbb{R}^+)^2}}) . .
Maintenant, si on prend  : x_i=0) on doit avoir on doit avoir =f(0)^m) et donc et donc =0) ou ou =1) . .
De même, on tombe sur =0) ou ou =1) . .
On discute maintenant les quatre cas possibles:
*Le premier cas: =f(0)=0) . .
On aura directement  , et par conséquent f est intégralement nulle. , et par conséquent f est intégralement nulle.
Ce qui vient en contradiction avec le fait que \neq{0}) . .
*Le second cas: =1) et et =0) . .
Tout de suite, on aura 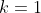 et et 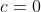 , et par conséquent , et par conséquent :f(x)=x) . .
Ce qui vient en contradiction avec le fait que \neq{2004}) . .
*Le troisième cas: =0) et et =1) . .
On aura donc 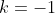 et et 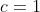 , et il s'ensuit que , et il s'ensuit que :f(x)=-x+1) . .
Dans ce cas, f n'est pas définie sur 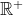 . .
(Le côté gauche de l'équation fonctionnelle de départ est positif, le côté droit doit l'être ainsi. Ainsi f est à valeurs dans l'ensemble des réels positifs)
*Le quatrième cas: =f(0)=1) . .
On aura donc 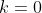 et et 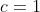 , et il s'ensuit que , et il s'ensuit que :f(x)=1) . .
Dans ce cas, =1) . D'où la conclusion. . D'où la conclusion.
Sauf erreurs.
P.S:J'ai souffert avec ce problème, et je serai reconnaissant si quelqu'un indique s'il y avait des fautes. l'equation de Jensen devrait être plutôt avec les variable  tu aura donc =\frac{f(\alpha&space;_1)+f(\alpha&space;_2)}{2}) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 | |
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 22 Avr 2012, 14:39 Dim 22 Avr 2012, 14:39 | |
| salut , @nmo concernant l'équation de jensen , tu as dit : ''dont les solutions sont les fonctions affines sur l'ensemble des rationnel '' mais la en travaille sur R | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 22 Avr 2012, 15:58 Dim 22 Avr 2012, 15:58 | |
| - Oty a écrit:
- salut , @nmo concernant l'équation de jensen , tu as dit : ''dont les solutions sont les fonctions affines sur l'ensemble des rationnel '' mais la en travaille sur R
Si l'équation de Jensen est valable sur l'ensemble des réels, elle doit l'être aussi pour tout ensemble qui lui appartient. Et nous pouvons nous contenter aux nombres rationnels, voire aux nombres entiers naturels qui nous intéresse. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 22 Avr 2012, 19:03 Dim 22 Avr 2012, 19:03 | |
| mais x et y sont des réels , il y a que m et n qui sont des entier , je n'ai pas bien compris ton raisonnement ? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 22 Avr 2012, 19:07 Dim 22 Avr 2012, 19:07 | |
| - Oty a écrit:
- mais x et y sont des réels , il y a que m et n qui sont des entier , je n'ai pas bien compris ton raisonnement ?
Tout ce que je veut dire est le suivant: Si on a \in{(\mathbb{R}^+)^2}}):f\bigg(\frac{x+y}{2}\bigg)=\frac{f(x)+f(y)}{2}) , alors \in{(\mathbb{N}^+)^2}}):f\bigg(\frac{x+y}{2}\bigg)=\frac{f(x)+f(y)}{2}) . N'est ce pas? | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 22 Avr 2012, 19:13 Dim 22 Avr 2012, 19:13 | |
| A vrai dire, je pense qu'on a pas le droit de donner des valeur concrète à m ou n parce qu’il sont fixe dans l’énoncé,donc on ne peut pas se contenter de considérer la cas ou n=2. Je pense plutôt à une récurrence pour prouver que l’équation: \in{(\mathbb{R}^+)^n}}):f(\frac{\alpha_{1}+\cdots+\alpha_{n}}{n})=\frac{f(\alpha_1)+\cdots+f(\alpha_n)}{n}) se réduit en l’équation de Jensen. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  Dim 22 Avr 2012, 19:57 Dim 22 Avr 2012, 19:57 | |
| - boubou math a écrit:
- A vrai dire, je pense qu'on a pas le droit de donner des valeur concrète à m ou n parce qu’il sont fixe dans l’énoncé,donc on ne peut pas se contenter de considérer la cas ou n=2.
Tu m'as eu. Au fait j'ai cru que la relation est valable pour n'importe quel entier n. - boubou math a écrit:
- Je pense plutôt à une récurrence pour prouver que l’équation:
\in{(\mathbb{R}^+)^n}}):f(\frac{\alpha_{1}+\cdots+\alpha_{n}}{n})=\frac{f(\alpha_1)+\cdots+f(\alpha_n)}{n})
se réduit en l’équation de Jensen. Voici une autre autoroute pour démontrer que f est affine: Notons que cette dernière équation fonctionnelle implique que si  est solution, alors est solution, alors  est aussi une solution (où est aussi une solution (où \in{(\mathbb{R}^+)^2}}) ). ).Il est judicieux de supposer que g(0)=0 où g est une solution éventuelle de cette équation. Si on prends :\alpha_i=0) et  , on aura :g(\frac{p}{n})=\frac{g(p)}{n}) . Du coup, \in{(\mathbb{R}^+)^n}}):g(\frac{\alpha_{1}+\cdots+\alpha_{n}}{n})=\frac{g(\alpha_1+\cdots+\alpha_n)}{n}) . Et donc \in{(\mathbb{R}^+)^n}}):\frac{g(\alpha_1+\cdots+\alpha_n)}{n}=\frac{g(\alpha_1)+\cdots+g(\alpha_n)}{n}) , ou encore \in{(\mathbb{R}^+)^n}}):g(\alpha_1+\cdots+\alpha_n)=g(\alpha_1)+\cdots+g(\alpha_n)) . On prends de nouveau :\alpha_i=0) et  et  , on doit avoir \in{(\mathbb{R}^+)^2}}):g(x+y)=g(x)+g(y)) . Ainsi g est solution de l'équation fonctionnelle de Cauchy, elle est donc affine sur l'ensemble des nombres rationnels. On en déduit que l'ensemble des solutions, en vertu de ce qui est souligné, est constitué des fonctions affines sur l'ensemble des nombres rationnels. On se contente après à définir f sur l'ensemble des entiers naturels. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012: Sujet: Re: Le dernier jeu pour la préparation aux IMOs 2012:  | |
| |
|
  | |
| | Le dernier jeu pour la préparation aux IMOs 2012: |  |
|
