- fmsi a écrit:
- calculez
lim(x tend vers 0) (x-tanx)/(x-sinx)
On doit calculer la limite:
}}{x-\sin{(x)}}\bigg))
.
On pose
=x-\tan{(x)})
et
=x-\sin{(x)})
.
Avec
=0-\tan{(0)}=0-0=0)
et
=0-\sin{(0)}=0-0=0)
.
De plus, les deux fonctions

et
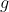
sont définies au voisinage de

.
Soit
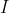
un intervalle pointié de centre

.
Les deux fonctions

et
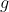
sont dérivables sur cet intervalle, car chacune est la combinaison linéaire de la fonction identité ( dérivable sur
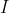
) et d'une fonction trigonométrique (la fonction sinus et la fonction tangentes sont dérivables sur
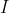
).
Et ainsi, on a les deux résultats suivants:
-
:f'(x)=(x-\tan{(x)})'=(x)'-(\tan{(x)})'=1-\frac{1}{\cos^2{(x)}})
.
-
:g'(x)=(x-\sin{(x)})'=(x)'-(\sin{(x)})'=1-\cos{(x)})
.
On passe maintenant à la limite:
}}{x-\sin{(x)}}\bigg)&=\lim_{x\to 0}\bigg(\frac{f(x)}{g(x)}\bigg)\\&=\lim_{x\to 0}\bigg(\frac{f(x)-f(0)}{g(x)-g(0)}\bigg)\\&=\lim_{x\to 0}\bigg(\frac{f(x)-f(0)}{x}\times\frac{x}{g(x)-g(0)}\bigg)\\&=\lim_{x\to 0}\bigg(\frac{f(x)-f(0)}{x-0}\times\frac{x-0}{g(x)-g(0)}\bigg)\\&=\lim_{x\to 0}\bigg(\frac{f(x)-f(0)}{x-0}\bigg)\times\lim_{x\to 0}\bigg(\frac{x-0}{g(x)-g(0)}\bigg)\\&=f'(0)\times\frac{1}{g'(0)}=\frac{f'(0)}{g'(0)}\\&=\lim_{x\to 0}\bigg(\frac{f'(x)}{g'(x)}\bigg)\\&=\lim_{x\to 0}\bigg(\frac{1-\frac{1}{\cos^2{(x)}}}{1-\cos{(x)}}\bigg)\\&=\lim_{x\to 0}\bigg(\frac{\frac{\cos^2{(x)}-1}{\cos^2{(x)}}}{-(\cos{(x)}-1)}\bigg)\\&=-\lim_{x\to 0}\bigg(\frac{\frac{(\cos{(x)}-1)(\cos{(x)}+1)}{\cos^2{(x)}}}{\cos{(x)}-1}\bigg)\\&=-\lim_{x\to 0}\bigg(\frac{\cos{(x)}+1)}{\cos^2{(x)}}\bigg)\\&=-\frac{\cos{(0)+1}}{\cos^2{(0)}}=-\frac{1+1}{1}=-2\end{align*})
.
Ce qui achève la preuve.
Sauf erreur.
P.S: il s'agit ici d'une application de la règle de l'hopital.
