Le dernier jeu pour la préparation aux IMOs 2012:

Mais les alpha i sont des réel est non des rationnels

Oty a écrit:

Mais les alpha i sont des réel est non des rationnels

Mais pour résoudre l'équation fonctionnelle de Cauchy dans l'ensemble des réels, il nous faut d'autres conditions tel que la continuité ou la monotonie...
Ici, ces données sont absentes: on ne peut résoudre l'équation fonctionnelle qu'en l'ensemble des rationnels.
Est ce que c'est clair? Est ce que j'ai tort?

tu as déja prouver un truc qui te permet d'affirmer que f est affines sur tout R d'apres l'equation de Cauchy , mais je vois que tu t'en es pas rendu compte .... cette condition tel que la continuité tu l'as

Oty a écrit:

tu as déja prouver un truc qui te permet d'affirmer que f est affines sur tout R d'apres l'equation de Cauchy , mais je vois que tu t'en es pas rendu compte .... cette condition tel que la continuité tu l'as

Où exactement? Je ne vois pas que f est continue.
Peux tu détailler s'il te plait?

f n'est pas continue mais elle est minoré .

Oty a écrit:

f n'est pas continue mais elle est minoré .

Oui, c'est ça! Je pense ainsi que le reste de ma solution est juste.
Voici le problème courant:

nmo a écrit:

En attendant une confirmation, je propose un nouveau problème:
Problème 22:
Déterminez tous les entiers n satisfaisant .
(E étant la fonction partie entière.)
Bonne chance.

Si vous permettez que je réponde à ce problème , car un truc me paraît bizarre :
Il existe deux suite (a_(n))n et (b_(n))n d'entiers telle que : (2+V(2))^(n)=a_(n)+V2b_(n) on a donc (2-V(2))^(n)=a_(n)-b_(n) et du coup
(2+V(2))^(n)+(2-V(2))^(n)= 2*a_(n) .
De plus pour tout n de N 0<(2-V(2))^(n)<1 donc pour tout n de N
2a_(n)-1<(2+V(2))^(n)<2a_(n) d’où :
E( (2+V(2))^(n)) = 2*a_(n)-1 est toujours impair
donc la seul solution est n=0 . Ma question est pourquoi 112 ?? Pourquoi 42 ou autre chose ??

darkpseudo a écrit:

Si vous permettez que je réponde à ce problème , car un truc me paraît bizarre :
Il existe deux suite (a_(n))n et (b_(n))n d'entiers telle que : (2+V(2))^(n)=a_(n)+V2b_(n) on a donc (2-V(2))^(n)=a_(n)-b_(n) et du coup
(2+V(2))^(n)+(2-V(2))^(n)= 2*a_(n) .
De plus pour tout n de N 0<(2-V(2))^(n)<1 donc pour tout n de N
2a_(n)-1<(2+V(2))^(n)<2a_(n) d’où :
E( (2+V(2))^(n)) = 2*a_(n)-1 est toujours impair
donc la seul solution est n=0 . Ma question est pourquoi 112 ?? Pourquoi 42 ou autre chose ??

Il parait qu'on ne peut pas avoir qu'un entier pair divise un autre qui est impair.
Ce qui impliquerait la contradiction si n n'était pas nul, alors forcément il est nul.
Ainsi, 112 peut être remplacé par 42 ou 38 ou tout autre entier pair.
(Ces remarques aideront à laisser l'exercice abordable et moins difficile, car par exemple si 112 est remplacé par 3 ou 7 l'exercice deviendra trop difficile)

non mais c'est juste que n'importe quelle entier pair aurait fait l'affaire alors pourquoi pas un numéro qui à un sens , bref c'est une remarque métaphysique XD . Et puis bonne chance à vous pour les imos , tu peux reposter un exo si tu veux "nmo" .

Je propose:
Problème 23:
Soient m et n deux entiers relatifs tels que est un entier relatif.
Déterminez la parité de .
Bonne chance.
P.S: Cher darkpseudo, attends mon prochain post dans la rubrique "Arithmétique"! J'ai un cadeau pour toi.

Ok en attendant ton post :
Problème 23 :

On a mod 3 ; (m+3)^(n)=-1 => m^(n)=-1 => n impair et 3 ne divise pas m .
Si m est impair on a (m+3)^(n)+1 est impair donc tout est impair .
Si m=2[4] on a (m+3)^(n)+1=2[4] et donc v2(A)=v2((m+3)^(n))-v2(3m) = 0 A est impair .
Si m=0[4] m+3+1=0[4] ( n est impair ) et on peut appliquer LTE http://www.artofproblemsolving.com/Resources/Papers/LTE.pdf .
on a donc : v2(A)=v2(m+4)-v2(m) si m=0[8] alors A est impair
le dernier cas donne A pair ( ce cas est possible par exemple pour m=-4)

Je propose encore un problème d'arithmétique:
Problème 24:
Démontrez que si l'équation admette des solutions dans l'ensemble des entiers naturels, alors .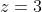
Bonne chance.

Solution du 24 :
Je propose de résoudre carrément l'équation ( sauf erreur de ma part ) :
considérant cette équation comme une équation du second degré en x on a donc deux racines .
La première c'est y , la seconde vérifie :
a+y=xyz et ay=(y^(2)+1).
ERREUR .

darkpseudo a écrit:

Ok en attendant ton post :
Problème 23 :
On a mod 3 ; (m+3)^(n)=-1 => m^(n)=-1 => n impair et 3 ne divise pas m .
Si m est impair on a (m+3)^(n)+1 est impair donc tout est impair .
Si m=2[4] on a (m+3)^(n)+1=2[4] et donc v2(A)=v2((m+3)^(n))-v2(3m) = 0 A est impair .
Si m=0[4] m+3+1=0[4] ( n est impair ) et on peut appliquer LTE http://www.artofproblemsolving.com/Resources/Papers/LTE.pdf .
on a donc : v2(A)=v2(m+4)-v2(m) si m=0[8] alors A est pair
le dernier cas donne A pair ( ce cas est possible par exemple pour m=-4)

Pour perfectionner ton travail, l'avant dernier cas doit être détaillé:
En effet, si , on aura car n est impair ainsi que m peut s'écrire de la forme m=4k+2 (ce qui donnera m+4=4k+2+4=4k+6=2(2k+3); i.e: l'exposant de 2 dans la décomposition de m+4 est 1).
En outre (de même m=4k+2 donnera 3m=2(6k+3); i.e: l'exposant de 2 dans la décomposition de 3m est aussi 1).
Ce qui donnera finalement .

darkpseudo a écrit:

Solution du 24 :
Je propose de résoudre carrément l'équation ( sauf erreur de ma part ) :
considérant cette équation comme une équation du second degré en x on a donc deux racines .
La première c'est y , la seconde vérifie :
a+y=xyz et ay=(y^(2)+1).
Donc , a = y+1/y on alors : 2y+1/y=xyz donc :
2y^(2)+1=xy^(2)z donc y^(2)*(xz-2)=1 donc y^(2)=1 et xz=3 mais l’équation étant symétrique on a le même résultat pour x d’où z=3 et les seuls solution sont les solutions triviales . Un fait assez sympas c'est que pour tout p premier >2 cette équation admet au moins p solutions différentes mod p ( Théorème de Chevalley-Warning) . Sauf erreur de ma part .

y n'est pas solution de l'équation que tu proposes.
L'exercice est loin d'être trivial, je pense.

Effectivement j'ai dis n'importe quoi sur le 24; ( pour l'exo d'avant c'était juste une faute de frappe ) ; alors je reprends le 24 :
l'équation X^(2)-Xyz+y^(2)+1 = 0 d'inconnue X admet x comme solution l'autre solution vérifie :
a+x=yz , ax=y^(2)+1 donc supposons que z différent de 3 et soit (x,y) un couple solution pour lequel x+y est minimal supposons aussi sans perte de généralité que y=<x on a donc a = (y^(2)+1)/x =<x+1/x or a est un entier donc a =< x ( si x différent de 1 ) , mais alors a=x par minimalité de (x,y) 2x=yz et x^(2)=y^(2)+1 => y=sqrt(x^(2)-1) donc 4x^(2)-z^(2)(x^(2)-1)=0 =>
z^(2)=(z^(2)-4)x^(2) or z est un entier naturel , on a et z^(2)-4 | 4 donc z^(2)-4=1 ou z^(2)-4 =2 ou z^(2)-4 =4 dans tout les cas z n'est pas un entier .
si x = 1 alors on a a=1 ou a=2 . Si a = 1 on a : 2=yz , 1=y^(2)+1. Si a=2 alors 3=yz , 2=y^(2)+1 => z=3 contradiction dans tout les cas . Sauf erreur .

darkpseudo a écrit:

Effectivement j'ai dis n'importe quoi sur le 24; ( pour l'exo d'avant c'était juste une faute de frappe ) ; alors je reprends le 24 :
l'équation X^(2)-Xyz+y^(2)+1 = 0 d'inconnue X admet x comme solution l'autre solution vérifie :
a+x=yz , ax=y^(2)+1 donc supposons que z différent de 3 et soit (x,y) un couple solution pour lequel x+y est minimal supposons aussi sans perte de généralité que y=<x on a donc a = (y^(2)+1)/x =<x+1/x or a est un entier donc a =< x ( si x différent de 1 ) , mais alors a=x par minimalité de (x,y) 2x=yz et x^(2)=y^(2)+1 => y=sqrt(x^(2)-1) donc 4x^(2)-z^(2)(x^(2)-1)=0 =>
z^(2)=(z^(2)-4)x^(2) or z est un entier naturel , on a et z^(2)-4 | 4 donc z^(2)-4=1 ou z^(2)-4 =2 ou z^(2)-4 =4 dans tout les cas z n'est pas un entier .
si x = 1 alors on a a=1 ou a=2 . Si a = 1 on a : 2=yz , 1=y^(2)+1. Si a=2 alors 3=yz , 2=y^(2)+1 => z=3 contradiction dans tout les cas . Sauf erreur .

Maintenant, c'est bon.
Une autre solution est de voir que 3 est le seul entier qui peut s'écrire de la forme .
C'est à toi de proposer maintenant. Ou bien, que quelqu'un d'autre prend l'initiative.

De toute façon ça revient à du Vieta-jumping , Je propose un exo pas très évident , je posterai une indication si personne ne trouve :
Problème 25 :
Soit E={3,5,7,11,13,17} et 50 réels a_(i) i dans [|0..49|] tels que pour tout p dans E et tout r entier on a sum a_(i) ( i=r mop p ) = sum a_(i) (i=0 mod p ) .
montrez que tout les a_(i) sont nuls .
Indice

Spoiler:

darkpseudo a écrit:

De toute façon ça revient à du Vieta-jumping , Je propose un exo pas très évident , je posterai une indication si personne ne trouve :
Problème 25 :
Soit E={3,5,7,11,13,17} et 50 réels a_(i) i dans [|0..49|] tels que pour tout p dans E et tout r entier on a sum a_(i) ( i=r mop p ) = sum a_(i) (i=0 mod p ) .
montrez que tout les a_(i) sont nuls .
Indice

Spoiler:

Je pense que le problème reste encore assez ardu, même avec l'indice (que je ne sais pas où l'utiliser).
Je t'invite à le changer et merci.

Ce n'est pas une raison pour le changer je trouve...
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=56&t=476954

momo1729 a écrit:

Ce n'est pas une raison pour le changer je trouve...
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=56&t=476954

Bien! On a bien utilisé l'indice de darkpseudo dans la seconde solution.
Maintenant, pour continuer, je t'invite à proposer un exercice.
Si ce n'est pas fait avant que je revienne la prochaine fois ici au forum, je proposerai moi même.

On a même pas besoin de polynômes cyclotomiques , on trouve un polynôme de degré 49 avec 50 racines , il est nul .
Exo :
Plus facile , sois ABC un triangle A' et B' les milieux de [BC] et [AC] , M le point d'intersection de (AA') et (BB') ; A'MB'C est CIRCONSCRIPTIBLE , montrez que ABC est isocèle .

Apparemment, je risque de me faire lyncher si je propose pas un problème dans les dix minutes qui suivent
Bon, le voilà :
Calculer
avec la partie entière de x.

Spoiler:

momo1729 a écrit:

Calculer
avec la partie entière de x.

Je ne propose pas une solution complète, mais le début:
On pose premièrement .
La division euclidienne de l'entier a sur l'entier b nous donne 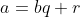où et .
Cela motive la procédure de diviser 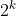par 2011, On aura ainsi: où et .
En sommant, il vient .
Dès lors, si je sais calculer c'est fini.
C'est là où je bloque et je ne sais pas comment utiliser l'indice donnée.
Et ce serait génial si quelqu’un achève cette preuve.

Salut
Tu peux trouver une solution très similaire à la tienne ici : http://www.artofproblemsolving.com/Forum/viewtopic.php?f=56&t=476229
Et la solution de "yunxiu" est la meilleure !

momo1729 a écrit:

Salut
Tu peux trouver une solution très similaire à la tienne ici : http://www.artofproblemsolving.com/Forum/viewtopic.php?f=56&t=476229
Et la solution de "yunxiu" est la meilleure !

Merci de m'expliquer comment pco a pu passer du fait que au résultat ?
Merci d'avance!