| | Jeu d'Hiver 2011-2012.(préparation aux olympiade) |  |
|
+19Oty stof065 Nayssi hind nassri Ahmed Taha (bis) ryuuzaki omra ali-mes amigo-6 yasserito manazerty rimele az360 judicecharatein Misterayyoub diablo902 Mehdi.O expert_run ZYGOTO boubou math 23 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sam 14 Avr 2012, 20:24 | |
| - diablo902 a écrit:
- Bonsoir,
Problème 11 reste sans solution
P#12: (VasC)
%20\in%20\mathbb{R}^+)
Prouver que si a²+b²+c²+d²=1 alors
(1-b)(1-c)(1-d)%20\ge%20abcd)
Bonne chance Je remarque qu'il y a un tas de discussion et de préparation. Et si un sujet est bloqué par un exercice difficile, on peut changer de terrain... Je propose une solution à cette inégalité: **Je démontre premièrement un lemme important: Si r et s sont deux réels positifs alors on a l'inégalité ^2}+\frac{1}{(1+s)^2}\ge\frac{1}{1+rs}) . Après des calculs et des simplifications, on voit qu'elle équivaut à \ge2rs+(rs)^2) . Or, on a \ge1+2(rs)^2=1+(rs)^2+(rs)^2\ge2rs+(rs)^2) . Ce qui termine la preuve. **On revient maintenant à notre inégalité: On définit  ,  ,  et  . Ainsi, on trouve  ,  ,  et  La condition initiale s'écrit: ^2}=1) . Et on est amené à démontrer que  . On a les deux inégalités suivantes: ^2}+\frac{1}{(1+y)^2}\ge\frac{1}{1+xy}) et ^2}+\frac{1}{(1+t)^2}\ge\frac{1}{1+zt}) . En sommant, on doit obtenir ^2}\ge\frac{1}{1+xy}+\frac{1}{1+zt}) . Il s'ensuit que  . Et donc , ce qui met fin à la démonstration. Sauf erreurs. | |
|
| | |
Oty
Expert sup
Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sam 14 Avr 2012, 21:09 | |
| Bravo nmo  | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sam 14 Avr 2012, 21:09 | |
| Puisque la géométrie est la bête noire des olympiades et l'un de ses piliers, en voici un problème qui traite l'un de ses résultats: Problème 13:Soit ABC un triangle, et soient M, N et P trois points qui appartiennent respectivement à [AB], [BC] et [CA] de telle sorte que les droites (AM), (BN) et (CP) se coupent en un point H et que  . Démontrez que H est l'orthocentre du triangle ABC. Bonne chance. | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sam 14 Avr 2012, 21:20 | |
| - nmo a écrit:
Si r et s sont deux réels positifs alors on a l'inégalité . Je propose une démonstration alternative de cette inégalité par CS: (1+\frac{r}{s})\geq%20(1+r)^2\Rightarrow%20\frac{1}{(1+r)^2}\geq%20\frac{s}{(1+rs)(r+s)}) De même: ^2}\geq%20\frac{r}{(1+rs)(r+s)}) , la somme donne: ^2}+\frac{1}{(1+s)^2}\geq%20\frac{r+s}{(1+rs)(r+s)}=\frac{1}{1+rs}) . | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Dim 15 Avr 2012, 00:01 | |
| Solution au problème 13: Via la symétrie qui existe dans la figure, il suffit montrer que (BH) est perpendiculaire sur (AC). D'abord, il est facile de remarquer que les quadrilatères AMHP, BMHN et CPHN sont inscriptibles (  , et même chose pour les autres). Et puis, par une chasse d'angles facile, on démontre que le quadrilatère BMPC est inscriptible:  Donc:  , et puisque  , il s'en suit que:  , d'où: \perp&space;(AC)) . Problème 14: 1)- Calculer: ) . 2)- Considérons 13 réels distincts, montrer que parmi ces nombres, il existe deux a et b tel que:  | |
|
| | |
az360
Expert grade2
Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Dim 15 Avr 2012, 00:15 | |
| autre solution pour 13 :
c'est facile a voir que : AMHP et MHNB et PHNC sont inscriptibles et ca implique que :
ang(BMN) = C et ang(MNB) = A
alors les deux triangle BMN et ABC sont semblables et ca implique que : MB/BN = BC/AB
par suite les deux triangles ABN et CBM sont semblables . dou le resultat !!
Solution Probleme 14
les 12 nombres sont : x_1 , ... , x_12 .
notant : tan(pi\12) = 2-sqrt(3)
on peut diviser l'intervalle ]-PI\2 , PI\2[ en 12 intervalle .
alors il existe a_1 et a_2 tel que :
tan(a_1) = x_i , tan(a_2) = x_j et a_1 - a_2 inférieur a PI\12
alors : tan(a_1 - a_2) inférieur a 2-sqrt(3) . d'ou le resultat !!! | |
|
| | |
diablo902
Maître
Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Dim 15 Avr 2012, 12:25 | |
| Salut,
az360 m'a permet de poster le 15ème problème
Problème 15:
Soit ABC un triangle dont les trois angles sont aigus et soit H son orthocentre.
Les tangentes au cercle de diamètre BC issues du point A touchent le cercle aux points P et Q.
Montrez que P, Q et H sont colinéaires | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 19:44 | |
| - diablo902 a écrit:
- Salut,
az360 m'a permet de poster le 15ème problème
Problème 15:
Soit ABC un triangle dont les trois angles sont aigus et soit H son orthocentre.
Les tangentes au cercle de diamètre BC issues du point A touchent le cercle aux points P et Q.
Montrez que P, Q et H sont colinéaires La solution est dans le lien suivant: http://www.artofproblemsolving.com/Forum/viewtopic.php?p=1964606&sid=b0a8bc8c6b78ac4f6cfff4a576ec43e7#p1964606. Je propose d'oublier ce problème, car il était dur. Voici un nouveau problème abordable: Problème 16:Résolvez en 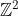 l'équation diophantienne suivante: (y^2+x)=(x-y)^3) . Bonne chance. | |
|
| | |
Siba
Maître
Nombre de messages : 143
Date d'inscription : 12/12/2011
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 20:45 | |
| On va trouver des solutions en fonction de k, ou juste 1 seule solution ? | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 20:48 | |
| - Siba a écrit:
- On va trouver des solutions en fonction de k, ou juste 1 seule solution ?
Ou est ce k, je ne le voit nulle part. | |
|
| | |
Siba
Maître
Nombre de messages : 143
Date d'inscription : 12/12/2011
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 20:58 | |
| Bah, normalement dans ce genre d'equations, on trouve un couple de solution en fonction d'un entier k de Z, par exemple (4k+3,7k+2), c'est le cas ici ?
Ou sinon, on doit trouver tous les couples d'entiers satisfaisant la relation ? | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 21:26 | |
| - Siba a écrit:
- Bah, normalement dans ce genre d'equations, on trouve un couple de solution en fonction d'un entier k de Z, par exemple (4k+3,7k+2), c'est le cas ici ?
Ou sinon, on doit trouver tous les couples d'entiers satisfaisant la relation ? Tu dois te débrouiller seul, propose ta methode et on verra. | |
|
| | |
Siba
Maître
Nombre de messages : 143
Date d'inscription : 12/12/2011
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 21:29 | |
| J'ai trouvé 6 cas à traiter, mais y en a que 2 qui sont bons: (3,0) et (0,-3).
| |
|
| | |
ryuuzaki omra
Maître
 Nombre de messages : 164
Age : 29
Localisation : Darna!
Date d'inscription : 17/12/2011
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 21:57 | |
| j'ai trouvé le couple (3y/y+3;y)! | |
|
| | |
Siba
Maître
Nombre de messages : 143
Date d'inscription : 12/12/2011
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 22:00 | |
| | |
|
| | |
ryuuzaki omra
Maître
Nombre de messages : 164
Age : 29
Localisation : Darna!
Date d'inscription : 17/12/2011
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 22:03 | |
| noooooooooooooooooo! je vais réessayer! | |
|
| | |
ryuuzaki omra
Maître
Nombre de messages : 164
Age : 29
Localisation : Darna!
Date d'inscription : 17/12/2011
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 22:05 | |
| | |
|
| | |
Siba
Maître
Nombre de messages : 143
Date d'inscription : 12/12/2011
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 22:15 | |
| je suis pas sur avoir traité tous les cas.. | |
|
| | |
ryuuzaki omra
Maître
Nombre de messages : 164
Age : 29
Localisation : Darna!
Date d'inscription : 17/12/2011
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 22:18 | |
| juste un seul cas je veux voir où j'ai fais la faute! Come on! | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 22:54 | |
| Solution proposé:- Spoiler:
Un carré parfait est toujours 0 mod 3 ou 1 mod 3.
* Si x-y \not\equiv 0[3][/img] par Fermat (x-y)^3=x-y[3]
-Supposons que x²=0[3] alors x=0[3] => y \not\equiv 0[3] alors y²=1[3]
Donc (x²+y)(y²+x)=y[3]*1[3]=y[3] alors y[3]=x-y[3] et donc 2y=x[3]
Or x=0[3] et donc 2y=0[3] ce qui est contradictoire avec y \not\equiv 0[3][/img] Et par symétrie on prouve que si y²=0[3] <=> y=0[3] il n'y aura pas de solutions.
-Si x²=1[3] alors y²=1[3]
Donc (x²+y)(y²+x) = (1+y)(1+x) [3] = x-y [3] ==> y(x+2)=2[3]
Et puisque x-y \not\equiv 0[3] alors : x=2[3] et y=1[3]. (1)
De plus, l'équation de départ <=> 2y^3+(xy)²+(xy)=3xy(x-y) <=> 2y^3=xy(3(x-y)-xy-1)
Si y=0 alors les couples solutions sont (m , 0) tel que m£IZ.
Si y se diffère de 0 alors 2y²=x(3(x-y)-xy-1) , et par (1) 3(x-y)-xy-1=0[3] donc 2y²=0[3] <=> y=0[3] chose qui se contredit avec le fait que y=1[3].
* Si 3|x-y alors x=y[3] donc l'équation de départ donne : (x²+x)²=0[3] donc x(x+1)=0[3]
Et alors x=0[3] ou x=2[3] , Si x=0[3] alors par 3|x-y on a y=0[3] et de même si x=2[3] alors y=2[3].
-Si x=2[3], on a 2y²=x(3(x-y)-xy-1) ,
-Si x=0[3] alors y=0[3] , on déduit l'existence de (k,k')£ IZ² / x=3k et y=3k'.
L'équation de départ devient: (3k²+k')(3k'²+k)=9(k-k')^3 donc 3|kk'
-Supposons que 3|k alors k=3m / m£IZ et 9*9m^3+3k'^3+9*9(mk')²+3mk'=9(3m-k')^3 (2)
donc 3|k'(k'²+3m) ===> 3|k' Et on aura : 9*9m^3+9*9m'^3+9*9*9(mm')²+9mm'=9*9(m-m')^3 ainsi 3|mm' ..
Ainsi de suite, on pourrait créer une suite infinie et strictement décroissante d'entiers naturels vérifiant (2). Absurde donc il n'existe pas d'entiers naturels non nuls x et y tels que
9*9m^3+3k'^3+9*9(mk')²+3mk'=9(3m-k')^3 Et alors pas de solution pour ce cas.
Conclusion: S={(m,0)/m£IZ}.
Dernière édition par M.Marjani le Mar 24 Avr 2012, 00:11, édité 1 fois | |
|
| | |
lamperouge
Maître
Nombre de messages : 133
Age : 28
Localisation : Casablanca
Date d'inscription : 13/01/2012
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 23:10 | |
| Une autre solution pour l'exo 16: On va utiliser la notion de derivabilite notons f(x)=(x-y)^3 /(x,y)£Z² et tel que y est un parametre et soit g(x)=(x²+y)(y²+x) g(x)=f(x) => g'(x)=f'(x) et puis g''(x)=f''(x) d'ou y=0 ou y=-3 On verifie facilement que -3 ne verifie po l'equation diophantienne et que pour y=0 l'equation est tjrs verifie d'ou S={(k,0)/k£Z} Sauf erreur | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 23:25 | |
| - M.Marjani a écrit:
- Solution proposé:
- Spoiler:
Un carré parfait est toujours 0 mod 3 ou 1 mod 3.
* Si x-y \not\equiv 0[3][/img] par Fermat (x-y)^3=x-y[3]
-Supposons que x²=0[3] alors x=0[3] => y \not\equiv 0[3] alors y²=1[3]
Donc (x²+y)(y²+x)=y[3]*1[3]=y[3] alors y[3]=x-y[3] et donc 2y=x[3]
Or x=0[3] et donc 2y=0[3] ce qui est contradictoire avec y \not\equiv 0[3][/img] Et par symétrie on prouve que si y²=0[3] <=> y=0[3] il n'y aura pas de solutions.
-Si x²=1[3] alors y²=1[3]
Donc (x²+y)(y²+x) = (1+y)(1+x) [3] = x-y [3] ==> y(x+2)=2[3]
Et puisque x-y \not\equiv 0[3] alors : x=2[3] et y=1[3]. (1)
De plus, l'équation de départ <=> 2y^3+(xy)²+(xy)=3xy(x-y) <=> 2y^3=xy(3(x-y)-xy-1)
Si y=0 alors les couples solutions sont (m , 0) tel que m£IZ.
Si y se diffère de 0 alors 2y²=x(3(x-y)-xy-1) , et par (1) 3(x-y)-xy-1=0[3] donc 2y²=0[3] <=> y=0[3] chose qui se contredit avec le fait que y=1[3].
* Si 3|x-y alors x=y[3] donc l'équation de départ donne : (x²+x)²=0[3] donc x(x+1)=0[3]
Et alors x=0[3] ou x=2[3] , Si x=0[3] alors par 3|x-y on a y=0[3] et de même si x=2[3] alors y=2[3].
-Si x=2[3], on a 2y²=x(3(x-y)-xy-1) alors y=0[3] contradiction avec y=2[3].
-Si x=0[3] alors y=0[3] , on déduit l'existence de (k,k')£ IZ² / x=3k et y=3k'.
L'équation de départ devient: (3k²+k')(3k'²+k)=9(k-k')^3 donc 3|kk'
-Supposons que 3|k alors k=3m / m£IZ et 9*9m^3+3k'^3+9*9(mk')²+3mk'=9(3m-k')^3 (2)
donc 3|k'(k'²+3m) ===> 3|k' Et on aura : 9*9m^3+9*9m'^3+9*9*9(mm')²+9mm'=9*9(m-m')^3 ainsi 3|mm' ..
Ainsi de suite, on pourrait créer une suite infinie et strictement décroissante d'entiers naturels vérifiant (2). Absurde donc il n'existe pas d'entiers naturels non nuls x et y tels que
9*9m^3+3k'^3+9*9(mk')²+3mk'=9(3m-k')^3 Et alors pas de solution pour ce cas.
Conclusion: S={(m,0)/m£IZ}.
Pourquoi on doit avoir ce qui est en rouge? | |
|
| | |
Oty
Expert sup
Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 23:28 | |
| salut , j'ai entendu dire que l'utilisation des fonctions dans les equation sur N n'est pas compté au oly c vrai ? | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 23:42 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Solution proposé:
- Spoiler:
Un carré parfait est toujours 0 mod 3 ou 1 mod 3.
* Si x-y \not\equiv 0[3][/img] par Fermat (x-y)^3=x-y[3]
-Supposons que x²=0[3] alors x=0[3] => y \not\equiv 0[3] alors y²=1[3]
Donc (x²+y)(y²+x)=y[3]*1[3]=y[3] alors y[3]=x-y[3] et donc 2y=x[3]
Or x=0[3] et donc 2y=0[3] ce qui est contradictoire avec y \not\equiv 0[3][/img] Et par symétrie on prouve que si y²=0[3] <=> y=0[3] il n'y aura pas de solutions.
-Si x²=1[3] alors y²=1[3]
Donc (x²+y)(y²+x) = (1+y)(1+x) [3] = x-y [3] ==> y(x+2)=2[3]
Et puisque x-y \not\equiv 0[3] alors : x=2[3] et y=1[3]. (1)
De plus, l'équation de départ <=> 2y^3+(xy)²+(xy)=3xy(x-y) <=> 2y^3=xy(3(x-y)-xy-1)
Si y=0 alors les couples solutions sont (m , 0) tel que m£IZ.
Si y se diffère de 0 alors 2y²=x(3(x-y)-xy-1) , et par (1) 3(x-y)-xy-1=0[3] donc 2y²=0[3] <=> y=0[3] chose qui se contredit avec le fait que y=1[3].
* Si 3|x-y alors x=y[3] donc l'équation de départ donne : (x²+x)²=0[3] donc x(x+1)=0[3]
Et alors x=0[3] ou x=2[3] , Si x=0[3] alors par 3|x-y on a y=0[3] et de même si x=2[3] alors y=2[3].
-Si x=2[3], on a 2y²=x(3(x-y)-xy-1) alors y=0[3] contradiction avec y=2[3].
-Si x=0[3] alors y=0[3] , on déduit l'existence de (k,k')£ IZ² / x=3k et y=3k'.
L'équation de départ devient: (3k²+k')(3k'²+k)=9(k-k')^3 donc 3|kk'
-Supposons que 3|k alors k=3m / m£IZ et 9*9m^3+3k'^3+9*9(mk')²+3mk'=9(3m-k')^3 (2)
donc 3|k'(k'²+3m) ===> 3|k' Et on aura : 9*9m^3+9*9m'^3+9*9*9(mm')²+9mm'=9*9(m-m')^3 ainsi 3|mm' ..
Ainsi de suite, on pourrait créer une suite infinie et strictement décroissante d'entiers naturels vérifiant (2). Absurde donc il n'existe pas d'entiers naturels non nuls x et y tels que
9*9m^3+3k'^3+9*9(mk')²+3mk'=9(3m-k')^3 Et alors pas de solution pour ce cas.
Conclusion: S={(m,0)/m£IZ}.
Pourquoi on doit avoir ce qui est en rouge? Salut cher nmo, On a déjà cité le cas de x²=0[3] et y²=0[3] il ne reste que x²=1[3] et y²=1[3]. | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Lun 23 Avr 2012, 23:44 | |
| - lamperouge a écrit:
- d'ou S={(k,0)/k£Z}
Sauf erreur et pour (8,-10) et (-1,-1) ? Voici des indications pour une autre démonstration: on développe les deux membres de l'équation , on factorise par y, on trouve le couple (k,0), pour l'autre équation on considère une équation du second degré, on fait la condition sur delta pour être un carré parfait , on trouve y, on remplace, et on trouve x. | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) | |
| |
|
| | |
| | Jeu d'Hiver 2011-2012.(préparation aux olympiade) | |
|
