| | Au Plaisir |  |
|
+5upsilon nmo darkpseudo Geo Top-Math 9 participants |
|
| Auteur | Message |
|---|
Top-Math
Féru
 Nombre de messages : 59 Nombre de messages : 59
Age : 27
Date d'inscription : 11/02/2012
 |  Sujet: Au Plaisir Sujet: Au Plaisir  Mer 18 Juil 2012, 23:23 Mer 18 Juil 2012, 23:23 | |
| Je propose donc ce sujet où on pourra proposer des exercices et les résoudre. C'est en gros un marathon d'été. Les règles sont connues :une personne qui propose une solution doit ensuite proposer un exercice et ainsi de suite. Bon je commence Problème 1 : a et b sont des entiers où PGCD(a,b)=1 Prouvez qu'il existe m et n de 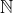 tel que  Bonne chance Bonne chance  | |
|
  | |
Geo
Habitué
 Nombre de messages : 24 Nombre de messages : 24
Age : 32
Date d'inscription : 13/07/2012
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Mer 18 Juil 2012, 23:46 Mer 18 Juil 2012, 23:46 | |
| Bonsoir, Solution au probleme 1:D'après le théorème d'Euler: }%20+b^{\varphi%20(a)}\equiv%201(\mod%20a%20)\\%20a^{\varphi%20(b)}%20+b^{\varphi%20(a)}\equiv%201(\mod%20b%20)%20\end{matrix}\right.\Rightarrow%20\left\{\begin{matrix}%20a%20|a^{\varphi%20(b)}%20+b^{\varphi%20(a)}-1\\%20b|a^{\varphi%20(b)}%20+b^{\varphi%20(a)}-1%20\end{matrix}\right.\Rightarrow%20ab%20|%20a^{\varphi%20(b)}%20+b^{\varphi%20(a)}-1%20\newline%20~~~~~~~~\Rightarrow%20m=\varphi(b),n=\varphi(a)) L'avant dernière implication est juste car PGCD (a,b)=1 Probleme 2:Si p un premier et a,b deux entiers tel que p |(4a²+1), Prouver que ) P.S: P.S:- Spoiler:
Joli problème AB-Math 
Dernière édition par Geo le Sam 21 Juil 2012, 15:03, édité 5 fois (Raison : Editer le 2eme probleme) | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 19 Juil 2012, 00:15 Jeu 19 Juil 2012, 00:15 | |
| pas besoin du 4, on peut généraliser à la somme de deux carrés. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Sam 21 Juil 2012, 22:00 Sam 21 Juil 2012, 22:00 | |
| - Geo a écrit:
- Probleme 2:
Si p un premier et a,b deux entiers tel que p |(4a²+1), Prouver que ) Je ne donne pas une réponse, mais je vais le faire dans mon prochain message. Avant d'être édité, le problème était ainsi: Démontrez que si p un premier et a,b deux entiers tel que  , alors ) . Ce problème manque de conditions supplémentaires, car on  et pourtant 3 n'est pas congru à 1 modulo 4... La condition qu'on doit ajouter peut être est que a et b n'ont aucun diviseur en commun sauf 1. (Bien entendu, ils doivent être tous les deux différent de 1 ou p est différent de 2). Un exercice similaire au tien est le suivant: Démontrez que si p est un nombre premier de la forme 4k+3 tel que  alors on doit forcément avoir  et  . Au plaisir! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Sam 21 Juil 2012, 22:29 Sam 21 Juil 2012, 22:29 | |
| - Geo a écrit:
- Probleme 2:
Si p un premier et a,b deux entiers tel que p |(4a²+1), Prouver que ) Supposons par l'absurde que p=2. On aura p divise 1 car p diviserai 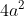 . Ce qui est clairement faux. Ainsi, puisque p est premier. Il est de la forme 4k+1 ou de la forme 4k+3. On suppose par l'absurde qu'on ait p de la forme 4k+3. Si p divise 2a alors p divise a selon le théorème de Gauss. Et par suite, on aura p divise 1. Ce qui vient en contradiction avec le fait que p est un entier premier. Ainsi =1) . Selon le petit théorème de Fermat, on aura ^{p-1}\equiv1(p)) ou encore ^{4k+2}\equiv1(p)) . Et puisque ^2+1\equiv0(p)) , alors ^2\equiv-1(p)) ou bien ^{4k+2}\equiv-(2a)^{4k}(p)) . Donc ^{4k}\equiv-1(p)) , et par suite ^{2k})^2\equiv-1(p)) d'où p ne divise pas ^{2k}) .==>(*) On applique encore une fois le petit théorème de Fermat pour avoir ^{2k})^{p-1}\equiv1(p)) . Donc ^{2k})^{4k+2}\equiv1(p)) soit ^{2k})^{4k}.((2a)^{2k})^2\equiv1(p)) . La dernière relation entraine que ^{2k})^2\equiv1(p)) ou encore ^{4k}\equiv1(p)) . Ce qui vient en contradiction avec *. On a eu une contradiction dans tous les cas, ce qui prouve que ) . CQFD. Sauf erreurs. | |
|
  | |
Geo
Habitué
 Nombre de messages : 24 Nombre de messages : 24
Age : 32
Date d'inscription : 13/07/2012
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Dim 22 Juil 2012, 13:22 Dim 22 Juil 2012, 13:22 | |
| | |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Dim 22 Juil 2012, 14:30 Dim 22 Juil 2012, 14:30 | |
| SalutVoici ma réponse à cet exo   On sait que p l (2a)²+1² donc p l (2a+1)² - 4a et p l (2a-1)² + 4a donc p l (2a+1)²+(2a-1)² D'où pr=(2a+1)²+(2a-1)² avec r nombre entier naturel
Par absurde
ContradictionD'où  Sauf erreur.... | |
|
  | |
ryuuzaki omra
Maître

 Nombre de messages : 164 Nombre de messages : 164
Age : 29
Localisation : Darna!
Date d'inscription : 17/12/2011
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Dim 22 Juil 2012, 14:54 Dim 22 Juil 2012, 14:54 | |
| Aide ! ba9i andi moshkil f l7isabiyate | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Mar 24 Juil 2012, 01:28 Mar 24 Juil 2012, 01:28 | |
| Voici un nouveau problème: Problème 3:Soit a, b et c des réels différents et non nuls tels que  . Déterminez la valeur de 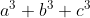 . Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Sam 28 Juil 2012, 22:30 Sam 28 Juil 2012, 22:30 | |
| - nmo a écrit:
- Voici un nouveau problème:
Problème 3:
Soit a, b et c des réels différents et non nuls tels que  . .
Déterminez la valeur de 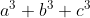 . .
Bonne chance. Il y a longtemps que j'ai proposé le problème, cependant je n'ai vu aucune tentative. Personnellement, j'ai trouvé que le problème est bizarre. En cherchant un peu, j'ai trouvé qu'il a vraiment un sens et une réponse. On a  , donc  . Ou en factorisant (a+b+\frac{1}{ab})=0) . Et vu que 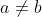 , on aura  . De même, on doit trouver  et  . On peut écrire  et  . Ce qui impliquerait forcément que  . Et ainsi  . Soit en factorisant encore (b+a+c)=0) . Par suite, il résulte que 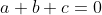 . Et on sait déjà que  . Donc  ou bien 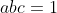 . En usant de l'identité remarquable \big((a-b)^2+(b-c)^2+(c-a)^2\big)) , de 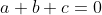 et de 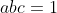 . On trouve finalement que  . Sauf erreurs. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Sam 28 Juil 2012, 23:37 Sam 28 Juil 2012, 23:37 | |
| Problème 4:Démontrez que :\sum_{i=2}^{n}\frac{1}{i}\notin\mathbb{N}) . Bonne chance. | |
|
  | |
Geo
Habitué
 Nombre de messages : 24 Nombre de messages : 24
Age : 32
Date d'inscription : 13/07/2012
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Dim 29 Juil 2012, 00:04 Dim 29 Juil 2012, 00:04 | |
| Bonsoir, Solution au problème 4:Soit k le maximum exposant tel que m= 2 kj ≤ n avec j un nombre impaire. Donc =2^ka) (avec a impaire).Alors :\sum_{i=2}^{n}\frac{1}{i}%20=%20\frac{1}{2}%20+..%20+%20\frac{1}{m}+..+\frac{1}{n}=\frac{2^{k-1}a+...+aj+..+2^k'a'\equiv1(\mod2)}{2^ka\equiv%200(\mod2%20)}%20\notin%20\mathbb{N}) . Sauf erreurs  Problème 5: Problème 5:Soient des entiers a,b >0. Prouver que si  alors %20\le%20\sqrt{a+b}) | |
|
  | |
Geo
Habitué
 Nombre de messages : 24 Nombre de messages : 24
Age : 32
Date d'inscription : 13/07/2012
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Mar 31 Juil 2012, 18:01 Mar 31 Juil 2012, 18:01 | |
| Solution au problème 5:d=Pgcd(a,b). On a d²|ab,a²,b² .  . Sauf erreurs. Problème 6:a,b,c et d des réels positives tel que a+b+c+d=4. Prouver que :  Bonne chance . | |
|
  | |
Geo
Habitué
 Nombre de messages : 24 Nombre de messages : 24
Age : 32
Date d'inscription : 13/07/2012
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 16 Aoû 2012, 01:38 Jeu 16 Aoû 2012, 01:38 | |
| Solution au problème 6:On a (x+y)²>=4xy <==> (x-y)²>=0 alors ^2%20\ge%204(a+b)(c+d)=4(ab+bc+cd+da)\Rightarrow%204\geq%20\sum%20ab%20\newline%20(\sum%20ab)^2%20\ge%204(ab+bc)(cd+da)=4\sum%20ab^2c\Rightarrow%20\sum%20ab\geq%20\sum%20ab^2c) D'après IAG:  Je n'ai pas de problème a proposer  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 16 Aoû 2012, 13:17 Jeu 16 Aoû 2012, 13:17 | |
| - Geo a écrit:
- Solution au problème 6:
On a (x+y)²>=4xy <==> (x-y)²>=0 alors
^2%20\ge%204(a+b)(c+d)=4(ab+bc+cd+da)\Rightarrow%204\geq%20\sum%20ab%20\newline%20(\sum%20ab)^2%20\ge%204(ab+bc)(cd+da)=4\sum%20ab^2c\Rightarrow%20\sum%20ab\geq%20\sum%20ab^2c)
D'après IAG:

Je n'ai pas de problème a proposer  Sauf une petite faute d'inattention dans la troisième ligne, on dirait un chef d’œuvre. Bravo! Je propose deux problèmes tirés de l'Irlande 2012; qui vont peut être proposé l'an prochain dans les tests et les stages: Problème 7:Trouvez tous les fonctions définies de l'ensemble des réels vers lui même et qui satisfont: \in\mathbb{R}^2): f(x+y.f(x))=f(x.f(y))-x+f(y+f(x))) . Problème 8:Trouvez tous les couples (x,y) qui vérifient l'équation suivante: (y-1)+8x(x-1)+2y(y-1)+3=0) . Bonne chance. | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 16 Aoû 2012, 15:39 Jeu 16 Aoû 2012, 15:39 | |
| Problème 8:
4xy(x-1)(y-1)+8x(x-1)+2y(y-1)+3=0
2y(y-1) ( 2x(x-1)+1 ) + 8x(x-1)+3=0
On pose a=4x(x-1)+2 >0 car 2x²-2x+1>0, qqs x
ay²-ay+2a-1=0
a²-4a(2a-1)=-7a²+4a=a(4-7a)<0 car 7a-4=28x²-28x+10>0
===> l'ensemble des (x,y) est vide
| |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 16 Aoû 2012, 17:16 Jeu 16 Aoû 2012, 17:16 | |
| salut , sa fait trés longtemps que je n'ai pas essayé de problème a part une inégalité , mais comme le topic chome un peu il faut y contribuer .
ma solution pour le Probleme 7 : de nmo
on a P(0,y) =>f(yf(0))=f(0)+f(y+f(0)) (1) de cette relation , supposant que f(0) est différent de 1 . alors P(0, f(0)\(f(0)-1))=> f(0)=0 . mais on remplacent cela dans (1) on a obtient :
f(y)=0 quelque soit y dans R qui n'est pas une solution , et par conséquent f(0)=1 , maintenant
P(x,0)=> f(f(x))=x quelque soit x .
P(1,y)=>f(1+yf(1))=y-1+f(y+f(1)) (2) . on prenant y=0 on a
f(1)=-1+f(f(1))=-1+1=0 et par conséquent en remplacent cela dans (2) on a
f(y)=1-y quelque soit y d'ou f(x)=1-x quelque soit x dans R qui est clairement solution .
| |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 16 Aoû 2012, 18:11 Jeu 16 Aoû 2012, 18:11 | |
| Problème 9 : Trouver la valeur maximal et minimal de : S=x+y dans le cas ou :  . | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 16 Aoû 2012, 19:03 Jeu 16 Aoû 2012, 19:03 | |
| Problème 9 :
u=V(x+1) et v=V(y+2) ==> S=u²+v²-3
la reletion <===> u²-1-3u=3v-v²+2
<===> (u-3/2)²+(v-3/2)²= 15/2
<==> le point (u,v) dans le cercle de centre (3/2,3/2) et de rayon V(15/2)=a
u=3/2+acos(t)
v=3/2+asin(t)
==>
S=(3/2+acos(t))²+(3/2+asin(t))²-3
= 9+3acos(t)+3asin(t) = 9+3V(15)sin(t+pi/4)
==> 9-3V(15)=<S=<9+3V(15) sauf erreur
| |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 16 Aoû 2012, 19:14 Jeu 16 Aoû 2012, 19:14 | |
| Bravo , le max est correcte mais le minime non ,
| |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 16 Aoû 2012, 19:27 Jeu 16 Aoû 2012, 19:27 | |
| Problème 10
Déteminer f définie sur R\{0,1} telle que qqs x dans R\{0,1} , f(x)+f((x-1)/x)=x+1 | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 16 Aoû 2012, 19:31 Jeu 16 Aoû 2012, 19:31 | |
| - Oty a écrit:
- Bravo , le max est correcte mais le minime non ,
C'est vrai (u,v) décrit le cercle en restant dans le quart du plan u>0 et v>0 | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 16 Aoû 2012, 20:48 Jeu 16 Aoû 2012, 20:48 | |
| - abdelbaki.attioui a écrit:
- Problème 10
Déteminer f définie sur R\{0,1} telle que qqs x dans R\{0,1} , f(x)+f((x-1)/x)=x+1 on remplace : x par (x-1)\x on obtient +f(\frac{1}{1-x})=\frac{2x-1}{x}) (2) on remplace x par 1\(1-x) dans (1) : +f(x)=\frac{2-x}{1-x}&space;(3)) (1) , (2) ,(3) nous donne un systeme de 3 equation ou il est facile d'isoler f(x) .... | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Jeu 16 Aoû 2012, 21:23 Jeu 16 Aoû 2012, 21:23 | |
| Probleme 11 : soit un triangle ABC non équilatéral AD , BE , CF ses hauteurs , sur les rayons AD , BE et CF respectivement on chois trois point : A1 , B1 , C1 vérifiant :  . Déterminer toute les valeurs de k pour que les triangles ABC et A1B1C1 soit semblables . Bonne chance . | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  Ven 17 Aoû 2012, 11:39 Ven 17 Aoû 2012, 11:39 | |
| - abdelbaki.attioui a écrit:
- Problème 9 :
u=V(x+1) et v=V(y+2) ==> S=u²+v²-3
la reletion <===> u²-1-3u=3v-v²+2
<===> (u-3/2)²+(v-3/2)²= 15/2
<==> le point (u,v) dans le cercle de centre (3/2,3/2) et de rayon V(15/2)=a
u=3/2+acos(t)
v=3/2+asin(t)
==>
S=(3/2+acos(t))²+(3/2+asin(t))²-3
= 9+3acos(t)+3asin(t) = 9+3V(15)sin(t+pi/4)
==> 9-3V(15)=<S=<9+3V(15) sauf erreur
Ici Max S=9+3V(15) atteint pour t=pi/4 Mais 9-3V(15) est juste un minorant. u et v sont postifs ==> t varie entre t0 et t1 tels que v(t0)=u(t1)=0 <==> cos(t0)=sin(t1)=-V(3/10) ==> Min S=S(t0)=S(t1) S(t0)=9-3V(15/2).V(3/10)+3V(15/2).V(1-3/10)=9-6+3V(21)/2=3+3V(21)/2 ==> Min S= 3+3V(21)/2 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Au Plaisir Sujet: Re: Au Plaisir  | |
| |
|
  | |
| | Au Plaisir |  |
|
