| | Retour au plaisir :) |  |
|
+33Othmaann MohE Xien ali-mes einstein20 sweet-mounir M.Marjani L'enfant ayoubmath phenix darkpseudo louis supista nmo houssa anas-az_137 stylo vs calculator marouan777 mizmaz Bison_Fûté Mr.Wajih m_zeynep Fermat-X just-abdess mathslover majdouline abdellah=einstein Dijkschneier Sporovitch amazigh-tisffola tarask meryem1994 Sylphaen 37 participants |
|
| Auteur | Message |
|---|
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Retour au plaisir :) Sujet: Retour au plaisir :)  Sam 23 Oct 2010, 18:10 Sam 23 Oct 2010, 18:10 | |
| Afin de se préparer un petit peu pour le prochain test qui aura lieu après un mois je crois ,je vous propose de commencer ce petit jeu classique. Les règles sont simples , qui résous un exo poste un autre , si celui ci n'est pas résolu pendant 48h on le change , et tacher de numéroter les exo's Pour commencer voici un simple exercice : Exercice 1 : Soit d,n des entiers strictement positif tels que d divise 2n² . Montrer que n²+d ne peut pas être un carré parfait . J'espère que vous serez nombreux à participer !  | |
|
  | |
meryem1994
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 44
Localisation : sin pi/2
Date d'inscription : 23/07/2008
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Sam 23 Oct 2010, 21:31 Sam 23 Oct 2010, 21:31 | |
| voilà une solution ke je propose pour cet exo
on suppose ke n²+d est un carre parfait
alors n²+d=A² alors a appartient à IN*
on a 2n²+d=k.d (k appart à IN* )
n²+d=A² ==> n²+2n²/k=A²
==> n²(1+2/k)=A²
si k=1 3n²=A²
si k=2 2n²=A²
si k>2 1+2/k n'appartient pa a IN*
alors n²+d n'est pas un carré parfait
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Dim 24 Oct 2010, 18:24 Dim 24 Oct 2010, 18:24 | |
| - meryem1994 a écrit:
- voilà une solution ke je propose pour cet exo
on suppose ke n²+d est un carre parfait
alors n²+d=A² alors a appartient à IN*
on a 2n²+d=k.d (k appart à IN* )
n²+d=A² ==> n²+2n²/k=A²
==> n²(1+2/k)=A²
si k=1 3n²=A²
si k=2 2n²=A²
si k>2 1+2/k n'appartient pa a IN*
alors n²+d n'est pas un carré parfait
ce qui est rouge est faux je crois  Tu as mal remplacé  | |
|
  | |
amazigh-tisffola
Expert grade1

 Nombre de messages : 487 Nombre de messages : 487
Age : 40
Localisation : kelaa m'gouna
Date d'inscription : 01/10/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Dim 24 Oct 2010, 19:08 Dim 24 Oct 2010, 19:08 | |
| salam
n^2+d=A^2 et d|2n^2 ==>il existe k£IN* tq 2n^2=k.d
.........................
on arrive a n^2(1+2/k)=A^2
pour k>0 on a 1+ 2/k£/IN
| |
|
  | |
meryem1994
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 44
Localisation : sin pi/2
Date d'inscription : 23/07/2008
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Dim 24 Oct 2010, 19:18 Dim 24 Oct 2010, 19:18 | |
| c pas ça ou se localise ma faute c'est plutot la ligne d'avant c'est une faute d'innatention e c tt | |
|
  | |
amazigh-tisffola
Expert grade1

 Nombre de messages : 487 Nombre de messages : 487
Age : 40
Localisation : kelaa m'gouna
Date d'inscription : 01/10/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Dim 24 Oct 2010, 19:35 Dim 24 Oct 2010, 19:35 | |
| - meryem1994 a écrit:
- c pas ça ou se localise ma faute c'est plutot la ligne d'avant c'est une faute d'innatention e c tt
meme la ligne d'avant tu paut changer just k par k+1 qui reste toujours dans IN, et ca marche | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Dim 24 Oct 2010, 19:54 Dim 24 Oct 2010, 19:54 | |
| Bonsoiir!! D'abord je tiens à remercier SYLPHAEN pour ce jeu, et j'aimerais bien que les participations soient vraiment au niveau ... (elles doivent être claires et compréhensibles) Ainsi je veux signaler qu'on doit varier les exercices pour essayer d'améliorer nos capacités dans tous les genres. en PLus, ce jeu va nous permettre de faire beaucoup d'exercices qui peuvent nous aider à bien maitriser une technique ou une méthode d'interet général. ENfin J'espere que les exercices qui seront proposés vont constituer un complément pour nous afin de bien confronter les tests d'olYmpiades. Un grand merci un Sylphaen. Soluion AU problem 1:puisque d|2n² ==> 2n²=kd ==> k²(n²+d)=n²k²+2n²k=n²((k+1)²-1) donc si n²+d est un carré parfait alors (k+1)²-1 est aussi un carré parfait donc il exitse un a tel que (k+1)²-1=a² <==> k+1-a=1 et k+1+a=1 ce qui est absurde!! Probleme 2:Résoudre dans IN le systeme suivant : | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Lun 25 Oct 2010, 19:03 Lun 25 Oct 2010, 19:03 | |
| Solution au problème 1 :d|2n², donc il existe un entier i tel que 2n²=id. Supposons qu'il existe un entier k tel que n²+d=k². => 2n²+2d=2k² => id + 2d = 2k² => d(i+2) = 2k² On a donc d(i+2)=2k² et id = 2n². Par produit, on a donc d²i(i+2)=(2nk)². Cela implique indubitablement que i(i+2) est un carré parfait. Par suite, i=0, et donc n=0. Et cela constitue une contradiction. Donc n²+d n'est jamais un carré parfait sous la condition d|2n². EDIT : simplification de la preuve. - Sporovitch a écrit:
Probleme 2:
Résoudre dans IN le systeme suivant :
 Merci d'indiquer la nature des variables employées.
Dernière édition par Dijkschneier le Mar 26 Oct 2010, 12:53, édité 1 fois | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Lun 25 Oct 2010, 19:46 Lun 25 Oct 2010, 19:46 | |
| Solution au problème 2 : Je crois x,y,z,n sont dans IN .. voici ma solution : - Spoiler:
On a : 3(x²+y²+z²)>(x+y+z)²>x²+y²+z² d'où : 5979 > n 4>1993 On déduit que : 8≥n≥7 Et puisque x²+y²+z² et x+y+z ont la même parité alors n est impaire et donc n=7 . Le système devient :  Du système on trouve que xy+yz+zx=204 Par symétrie on suppose que x≥y≥z , on a : 3x²≥1993 et x²<1993 d'où 44≥x≥26 . et on a : 204=xy+yz+zx≥3z² => 8≥z Aussi on a : xy+yz+zx≥y² => 14≥y Et : x²=1993-y²-z²≥1993-8²-14² =>x≥42 Encore : 49=x+y+z≥42+2z => 3≥z et 7≥y Finalement x²=1993-y²-z²≥1993-3²-7² =>x≥45 ( contradiction avec le fait que 44≥x ) Donc pas de solution pour le système ..
Exercice 3 : Soit n entiers a 1,a 2,...a n . Prouver qu'il existe un sous ensemble de {a 1,a 2,...a n } dont la somme est divisible par n. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Lun 25 Oct 2010, 20:38 Lun 25 Oct 2010, 20:38 | |
| Solution au problème 3 :Soient E et F deux ensembles tels que  et \}) . Supposons que l'un des éléments de E, disons 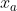 , soit divisible par n. Alors l'ensemble  répond bien au problème. Supposons désormais qu'aucun des éléments de E n'est divisible par n. Soit alors la fonction f qui envoie chaque entier vers son résidu modulo n. En vertu de la supposition faite, f est alors bien définie de E sur F. Et on a =n) et =n-1) . Selon le principe des tiroirs, il existe au moins deux éléments de E qui ont la même image par f. En d'autres termes, il existe deux éléments 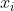 et 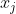 de E tels que i>j et que  . Et on a :  . L'ensemble  répond bien au problème. EDIT : correction de la preuve.
Dernière édition par Dijkschneier le Mar 26 Oct 2010, 12:55, édité 2 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Lun 25 Oct 2010, 20:47 Lun 25 Oct 2010, 20:47 | |
| Problème 4 :On note a,b et c les longueurs des côtés du triangle ABC, et R le rayon de son cercle circonscrit. Prouver que si ABC n'est pas obtus, alors : ^{\frac{1}{a}}(\frac{2\widehat{B}}{\pi})^{\frac{1}{b}}(\frac{2\widehat{C}}{\pi})^{\frac{1}{c}}%20\leq%20(\frac{2}{3})^{\frac{\sqrt{3}}{R}}) Quand est-ce que l'égalité a lieu ? | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Lun 25 Oct 2010, 22:34 Lun 25 Oct 2010, 22:34 | |
| Solution au problème 4 : ( à vérifier ) - Spoiler:
L'inégalité est équivalente à :    Posons :  La fonction f est concave sur ]0,pi/2] donc d'après Jensen on a :  Et le résultat en découle ...( égalité ssi a=b=c
Dernière édition par Sylphaen le Mar 26 Oct 2010, 13:21, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 26 Oct 2010, 12:51 Mar 26 Oct 2010, 12:51 | |
| Oui Sylphaen, mais la première ligne de ta démonstration me semble douteuse. Il doit y avoir un sigma ou bien un pi ? | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 26 Oct 2010, 13:25 Mar 26 Oct 2010, 13:25 | |
| Ouép , c'est édité ! =)
Problème 5 :
Soient (AL) et (BK) les bissectrices intérieur du triangle ABC ( non isocèle ) avec L £ [BC] et K £ [AC] .
La médiatrice de [BK] coupe (AL) en M . Et N est un point de (BK) tels que (LN) // (MK) .
Démontrer que : LN=NA | |
|
  | |
abdellah=einstein
Maître

 Nombre de messages : 110 Nombre de messages : 110
Age : 31
Localisation : taroudant
Date d'inscription : 07/03/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 27 Oct 2010, 01:14 Mer 27 Oct 2010, 01:14 | |
| bnsoir (svp si qq verifient ce que j'ai poster) - Spoiler:
j'espere que c'est la bonne reponse(dsl s'il ya une erreur) | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 27 Oct 2010, 15:52 Mer 27 Oct 2010, 15:52 | |
| Joli abdellah-einstein. A toi.
PS : si tu pouvais mieux expliquer ton (*) et ton PS, ce serait formidable. | |
|
  | |
abdellah=einstein
Maître

 Nombre de messages : 110 Nombre de messages : 110
Age : 31
Localisation : taroudant
Date d'inscription : 07/03/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 27 Oct 2010, 18:48 Mer 27 Oct 2010, 18:48 | |
| - Dijkschneier a écrit:
- Joli abdellah-einstein. A toi.
PS : si tu pouvais mieux expliquer ton (*) et ton PS, ce serait formidable. bonsoir merci pour ta confirmation Dijkschneier cette (*) c'est comme un tiret pour faire les deux cas sur les angles AKM et ABM pr le Ps c'est parce que dans des autres cas on va trvé que le point M est a l'interieur du triangle ABC par exemple tandis que dans ma solution j'ai traité seulemnt le cas ou M est a l'exterieur du triangle ABC et ce que j'ai essayé de dire que sois M a l'interieur de ABC ou a l'exterieur les deux quadrillatére AKMB et ANLB reste inscriptible en voici une petite probleme calculer la somme suivante  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Ven 29 Oct 2010, 14:34 Ven 29 Oct 2010, 14:34 | |
| bonjour.... solution du problème6:- Spoiler:
problème7:sachant que a+b+c=4 calculer le max de l'expression:  | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Ven 29 Oct 2010, 14:51 Ven 29 Oct 2010, 14:51 | |
| Bon après-midi  Solution du problème 7 Solution du problème 7- Spoiler:
considérons la fonction f définie sur I=[-1/2;+oo[ ainsi f(x)=√(2x+1) f est dérivable sur I\{-1/2} et f''(x) <0 d'où la concavité de f alors d'après l'inégalité de Jensen : f(a)+f(b)+f(c)=<3 f[(a+b+c)/3] D'où max A =√33 Sauf erreur biensur 
| |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Ven 29 Oct 2010, 14:54 Ven 29 Oct 2010, 14:54 | |
| - tarask a écrit:
- Bon après-midi

Solution du problème 7
- Spoiler:
considérons la fonction f définie sur I=[-1/2;+oo[ ainsi f(x)=√(2x+1) f est dérivable sur I\{-1/2} et f''(x) <0 d'où la concavité de f alors d'après l'inégalité de Jensen : f(a)+f(b)+f(c)=<3 f[(a+b+c)/3] D'où max A =√33 Sauf erreur biensur 
dsl tarsak ce n'est pas la bonne réponse f(b)=???? et f(c)=???? | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Ven 29 Oct 2010, 14:54 Ven 29 Oct 2010, 14:54 | |
| oops faute d'inattention  Désolé !! | |
|
  | |
mathslover
Habitué

 Nombre de messages : 27 Nombre de messages : 27
Age : 31
Date d'inscription : 29/10/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Ven 29 Oct 2010, 16:00 Ven 29 Oct 2010, 16:00 | |
| solution au probleme 7 sauf erreur  - Spoiler:
http://latex.codecogs.com/gif.latex?$x=%20\sqrt{2a+1}$%20$%20et%20$%20$%20y=\sqrt{3b+1}$%20$%20et$%20$%20z=\sqrt{4c+1}$.%20\Rightarrow%20a=\frac{x^{2}+1}{2}%20b=\frac{y^{2}-1}{2}%20c=\frac{z^{2}+1}{2}%20\Rightarrow%20$%20A=x+y+z$%20/%20\frac{x^{2}-1}{2}+\frac{y^{2}-1}{3}+\frac{z^{2}-1}{4}=4%20\Rightarrow%20\frac{x^{2}}{2}+\frac{y^{2}}{3}+\frac{z^{2}}{4}=\frac{61}{12}%20$%20Par%20C.S.%20on%20a%20$%20(2+3+4)(\frac{x^{2}}{2}+\frac{y^{2}}{3}+\frac{z^{2}}{4})\geq%20(x+y+z)^{2}%20\Rightarrow%20\sqrt{9\frac{61}{12}}%20\geq%20x+y+z%20\Rightarrow%20\sqrt{\frac{183}{4}}%20\geq%20x+y+z%20$donc%20la%20valeur%20max%20de%20A%20est%20$%20\sqrt{\frac{183}{4}}.
Dernière édition par mathslover le Ven 29 Oct 2010, 21:06, édité 1 fois | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Ven 29 Oct 2010, 20:03 Ven 29 Oct 2010, 20:03 | |
| Solution au probleme 7: - Spoiler:
 CQFD PS: cas d'égalité :a=17/27 ,b=49/36 ,c=217/108 !!
PROBLEME 8:On se donne des entiers naturels k<l<m<n tels que kn=ml Prouver que :  @mathsolver: - Spoiler:
on ne doit pas copier les solution des autres  et editer son message apres leur post
Dernière édition par Sporovitch le Ven 29 Oct 2010, 22:29, édité 2 fois (Raison : regler le probleme 8) | |
|
  | |
mathslover
Habitué

 Nombre de messages : 27 Nombre de messages : 27
Age : 31
Date d'inscription : 29/10/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Ven 29 Oct 2010, 22:11 Ven 29 Oct 2010, 22:11 | |
| @ Sporovitch - Spoiler:
@ Sporovitch : dsl mec mé j'é pas l'habitude de copier les solutions des autres et j'ai rien à faire avec  moi j'avais posté une solution avant la tienne sauf que j'é pas fé att et j'é travaillé avec 2a+1 et 2b+1 et 2c+1 quand j'ai fé att j'ai juste changé de num la methode est restée la meme et je t'ai rien dit quand t'as posté ton probleme"8" d'ailleurs moi j'ai posté toute la solution toi à peine le resultat alors stp la prochaine fois pas besoin de repprocher à qlq un klk chose qui touchent sa dignité ou son orgueil 
| |
|
  | |
mathslover
Habitué

 Nombre de messages : 27 Nombre de messages : 27
Age : 31
Date d'inscription : 29/10/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Ven 29 Oct 2010, 23:27 Ven 29 Oct 2010, 23:27 | |
| solution au prob 8: - Spoiler:
on a (n,m,l,k) € lN^4 tq n>m>l>k donc il existe a, b et c des entiers naturels tq a>b>c verifient k=k et l=k+c et m=k+b et n=k+a. on a l.m=n.k <=> (k+c)(k+b) = k(k+a) <=> k²+ck+bk+cb = k²+ak <=> k= (bc)/(a-b-c) on MQ (n_k)²/4 k+2 <=> a²/4 >= (bc)/(a-b-c) +2 en faisant le calcul ça va donner : <=> a^3 -a²(b+c) -8a +8(b+c) -4bc >= 0 pospns la fonction f tel que f(x) = x^3 -x²(b+c) -8x +8(b+c) -4bc (avec x€lN et x >= 4 même x>=0 ferra l'affaire) on calcule la dérivé : f'(x) = 3x²-2(b+c)x -8 ; delta = 4(b+c)² + 96 >0 x_1 = ( (b+c) - rac ( (b+c)² - 24) ) /3 strict positif x_2 = ((b+c) + rac ( (b+c)² - 24) ) /3 strict positif sur l'intervalle [0, x_1] croissante sur l'intervalle [x_1, x_2] décroissante sur l'intervalle [x_2, +l'infini] croissante avec f(0) > 0 et f(x_2) >0 ( les images" encore un peu de calcul " ) d'où le resultat . 
probleme 9 : soient x, y et z des reels positifs tels que x+y+z =< 1.
trouver la valeur maximale de l'expression T = xy+yz+xz -2xyz | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  | |
| |
|
  | |
| | Retour au plaisir :) |  |
|
