Retour au plaisir :)

Voici un nouveau problème:

Problème 89:

Soit a, b et c des réels positives, montrer que:

ali-mes a écrit:

Tu as inversé les rôles de E et F !
La prochaine fois, tu aurais au moins lire le problème.

Merci beaucoup pour cette observation monsieur ali-mes.. je vais éditer.

Voici un autre exercice que j'ai trouvé très intéressant :

Problème 90:

On colorie tous les points du plan avec ces trois couleurs: rouge, vert et bleu.

Montrer qu'il existe deux points P et Q tel que PQ=1 et P et Q ont la même couleur.

ali-mes a écrit:

Voici un nouveau problème:
Problème 89:
Soit a, b et c des réels positives, montrer que:

J'ai tant souffert avec cette inégalité, mais finalement je crois que j'ai trouvé la solution:
En guise de simplification, on pose: et .
Donc et .
L'inégalité s'écrit alors: , soit .
Ou encore .==>(*)
On a selon l'inégalité arithmético-géométrique les inégalités suivantes:
-, avec égalité si et seulement si .
-, avec égalité si et seulement si .
-, avec égalité si et seulement si .
En multipliant ces inégalités membre par membre, il vient que: .
Donc .
Avec égalité si et seulement si .
En s'aidant de l'identité suivante: , on aura:
.
Ainsi, selon *, il suffit de démontrer que: .
Donc .
Soit .
Ou encore, après la simplification par 8,.==>(**)
On a selon l'inégalité arithmético-géométrique les inégalités suivantes:
-, soit .==>(1)
Avec égalité si et seulement si , donc .
-, soit .
On a ainsi .==>(2)
Avec égalité si et seulement si , donc .
En sommant 1 et 2, on aura .
C'est à dire que .
Ce qu'il faut démontrer d'après **.
On a donc démontré que: .
Le cas d'égalité est lorsque et .
C'est à dire lorsque .
(La contrainte est une conséquence de ).
CQFD.
Sauf erreur.

ali-mes a écrit:

Voici un autre exercice que j'ai trouvé très intéressant :
Problème 90:
On colorie tous les points du plan avec ces trois couleurs: rouge, vert et bleu.
Montrer qu'il existe deux points P et Q tel que PQ=1 et P et Q ont la même couleur.

D'emblée, si on a utilisé une seule couleur, le problème est résolu.
De même, si on utilisé justement utilisé deux couleur.
On suppose maintenat que les trois couleurs sont utilisés.
On doit démontrer premièrement qu'il existe deux points distants de n'ayant pas la même couleur.
On suppose par l'absurde que que lorsque la distance entre deux points est , alors ces deux points ont la même couleur.
On considère un point M du plan.
On trace le cercle de centre M et de rayon .
Tous les points de ce cercle sont de la même couleur que M.
Maintenant, soit X un point de ce cercle.
On trace ensuite le cercle de centre X et de rayon .
Tous les points de ce cercle sont de la même couleur que X, et a fortiori que M.
Et ainsi de suite.
On démontre alors que le plan est colorié d'une même couleur.
Ce qui est absurde.
On conclût qu'il existe deux points distants de n'ayant pas la même couleur.
Soit A un point rouge et B un point bleu tel que .
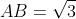
On trace le cercle de centre A et de rayon 1, et le cercle le cercle de centre B et de rayon 1.
Cest deux cercles se coupent en 2 point qu'on nomme I et J.
Il faut démontrer que: IJ=1.
La droite (IJ) est l'axe radical de ces deux cercles.
On note O leur point d'intersection des droites (AB) et (IJ).
Par conséquent, les droites (IJ) et (AB) sont perpendiculaires en O.
Ainsi que O est le milieu respectif des deux segments [AB] et [IJ].
Donc .
Et .
En utilisant le théorème de phytagore, on aura: .
Donc .
Soit .
D'où , et par conséquent IJ=1.
On se retrouve devant 3 cas:
-Cas premier: l'un des points I ou J est rouge.
Comme AI=1ou AJ=1, donc il existe 2 points rouge dont la distance est 1.
-Cas second: l'un des points I ou J est bleu.
Comme BI=1 ou BJ=1, donc il existe 2 points bleu dont la distance est 1.
-Cas troisième: les deux points I et J sont verts.
et comme IJ=1, alors il existe 2 points vert dont la distance est 1.
-Conclusion:
Dans tous les cas: il existe deux points P et Q tel que PQ=1 et P et Q ont la même couleur.
CQFD.
Sauf erreur.

Superbe nmo, tes deux réponses sont exemplaires.

A toi l'honneur de proposer un nouveau problème.

Je mêle inégalité et géométrie:
Problème 91:
Soit P un point intérieur à un triangle ABC.
Et A', B' et C' sont respectivement les projetés orthogonaux de P sur (BC), (AC) et (AB).
Montrez que: .
Bonne chance.

nmo a écrit:

Je mêle inégalité et géopmétrie:
Problème 91:
Soit P un point intérieur à un triangle ABC.
Et A', B' et C' sont respectivement les projetés orthogonaux de P sur (BC), (AC) et (AB).
Montrez que: .
Bonne chance.

Solution pour 91:

Figure:

Spoiler:

Démonstration:

Spoiler:

PS: Cette inégalité s'appelle le théorème d'Erdos-mordell.

Problème 92:
Trouver toutes les fonctions f:IR*+ --> IR+ tel que

PS: J'ai changé de problème.