| | Retour au plaisir :) |  |
|
+33Othmaann MohE Xien ali-mes einstein20 sweet-mounir M.Marjani L'enfant ayoubmath phenix darkpseudo louis supista nmo houssa anas-az_137 stylo vs calculator marouan777 mizmaz Bison_Fûté Mr.Wajih m_zeynep Fermat-X just-abdess mathslover majdouline abdellah=einstein Dijkschneier Sporovitch amazigh-tisffola tarask meryem1994 Sylphaen 37 participants |
|
| Auteur | Message |
|---|
mizmaz
Maître
 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Retour au plaisir :) Mer 15 Déc 2010, 14:50 | |
| - just-abdess a écrit:
- solution problème 54:
- Spoiler:
(sauf erreur)
problème 55:
soit _{n\epsilon&space;\mathbb{N}}) une suite definit par :
Montrer que
 Nous avons pour tout  : ^2=u_n^2+2+\frac{1}{u_n}) Donc :  Prouvons maintenant par récurrence que  Alors :  Et +25\Rightarrow%20u_{n+1}^2>%202(n+1)+25) Donc Pour n=1000  Sauf erreur. (Excusez la rédaction pourrie.) Au plaisir ! | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Retour au plaisir :) Mer 15 Déc 2010, 20:29 | |
| Problème 56 :On considère ) suite de nombres premiers telle que 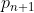 est le plus grand diviseur premier de  . Montrez que la suite est bornée. | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Retour au plaisir :) Mer 15 Déc 2010, 20:55 | |
| Solution fausse au problème 56 :La suite (pn) est minorée par 0. Montrons par récurrence forte qu'elle est majorée par un réel K. - Quitte à choisir K assez grand, p0 < K - Supposons que jusqu'au rang n, pn < K. Au rang n+1 :  , la dernière inégalité étant vraie pour K suffisamment grand. On a utilisé ici l'inégalité stipulant que le plus grand diviseur premier de n est inférieur à la racine carrée de n. EDIT : cette solution est fausse.
Dernière édition par Dijkschneier le Ven 17 Déc 2010, 19:54, édité 2 fois | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Retour au plaisir :) Mer 15 Déc 2010, 21:31 | |
| - Dijkschneier a écrit:
- Solution au problème 56 :
La suite (pn) est minorée par 0.
Montrons par récurrence forte qu'elle est majorée par un réel K.
- Quitte à choisir K assez grand, p0 < K
- Supposons que jusqu'au rang n, pn < K.
Au rang n+1 :  , la dernière inégalité étant vraie pour K suffisamment grand.
On a utilisé ici l'inégalité stipulant que le plus grand diviseur premier de n est inférieur à la racine carrée de n. Joli ! A toi. | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Retour au plaisir :) Mer 15 Déc 2010, 22:43 | |
| Problème 57 : (** : deux étoiles)
Trouver toutes les fonctions numériques (de IR vers IR) vérifiant pour tous x,y réels : f(x+f(y)) = f(x) + f(y)² + 2xf(y). | |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Retour au plaisir :) Jeu 16 Déc 2010, 13:02 | |
| - Dijkschneier (Mer 15 Déc 2010, 20:55) a écrit:
- Solution au problème 56 :
La suite (pn) est minorée par 0.
Montrons par récurrence forte qu'elle est majorée par un réel K.
- Quitte à choisir K assez grand, p0 < K
- Supposons que jusqu'au rang n, pn < K.
Au rang n+1 : , la dernière inégalité étant vraie pour K suffisamment grand.
On a utilisé ici l'inégalité stipulant que le plus grand diviseur premier de n est inférieur à la racine carrée de n. Je crois que c'est faux : n=255=3.5.17 Le plus grand diviseur premier de n est 17 >255^(0.5)
Dernière édition par Sylphaen le Jeu 16 Déc 2010, 13:05, édité 1 fois | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Retour au plaisir :) Jeu 16 Déc 2010, 13:04 | |
| - Sylphaen (Jeu 16 Déc 2010, 13:02) a écrit:
- Dijkschneier (Mer 15 Déc 2010, 20:55) a écrit:
- Solution au problème 56 :
La suite (pn) est minorée par 0.
Montrons par récurrence forte qu'elle est majorée par un réel K.
- Quitte à choisir K assez grand, p0 < K
- Supposons que jusqu'au rang n, pn < K.
Au rang n+1 : , la dernière inégalité étant vraie pour K suffisamment grand.
On a utilisé ici l'inégalité stipulant que le plus grand diviseur premier de n est inférieur à la racine carrée de n. Je crois que c'est faux :
n=340=2².5.17
Le plus grand diviseur premier de n est 17 < 340^(0.5) Je ne comprends pas ton contre-exemple. Enfin... c'en n'est pas un, je crois. | |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Retour au plaisir :) Jeu 16 Déc 2010, 13:06 | |
| Désolé , j'étais entrain d'éditer.. L'inégalité que Dijkschneier a utilisé est fausse . C'est plutôt le plus petit diviseur premier de n qui est inférieur à la racine de n . | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Retour au plaisir :) Jeu 16 Déc 2010, 13:10 | |
| Ah oui... Désolé, j'avais pas fait attention. On reprend alors.
Vraiment désolé. | |
|
| | |
supista
Féru
Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
| | Sujet: Re: Retour au plaisir :) Jeu 16 Déc 2010, 18:54 | |
| Solution du problème 56
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=56&t=382633&p=2120832#p2120832
| |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Retour au plaisir :) Ven 17 Déc 2010, 18:36 | |
| Solution au problème 57 : - Spoiler:
-Pour x=0 on a : f(f(y))=f(y)²+f(0) -Pour x=f(z)-f(y) / z £ IR on obtient : f(f(z)-f(y))= ( f(z)-f(y) )² +f(0) Si pour tous x , f(x)=0 alors f est la fonction nul qui réciproquement vérifie les donnés du problème . sinon il existe un réel k t.k f(k) est non nul . -Pour  et a un réel quelconque on obtient : f(x+f(y))-f(x)=a Donc , dans ce cas ,pour tous réel a il existe 2 réels b,c t.q : a=f(b)-f(c) Alors : f(a)=f(f(b)-f(c))=(f(b)-f(c))²+f(0)=a²+f(0) et réciproquement on vérifie que la fonction f(x)=x²+c est une solution du problème .. Donc les solutions du problème sont la fonction nul et la fonction x->x²+c / c £ IR .
Problème 58 : x 1,x 2...,x n ( n>2 ) sont des réel tels que :  Calculer en fonction de n :  | |
|
| | |
just-abdess
Maître
Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
| | Sujet: Re: Retour au plaisir :) Ven 17 Déc 2010, 21:05 | |
| Salut Solution du probleme 58 :- Spoiler:
par un simple calcule on trouve : }=&space;\Large&space;\sum_{k=1}^{n}{(2k-n-1)}) si n=2p }=&space;\Large&space;\sum_{k=1}^{2p}{(2k-2p-1)x_{k}}=(2p-1)x_{n}+....+x_{p+1}-x_{p}-...-(2p-1)x_{1}=(2p-1)(x_{2p}-x_{1})+(2p-3)(x_{2p-1}-x_{2})+...+(2p-(2p-1))(x_{p+1}-x_{p})\leq&space;2p^{2}-(1+3+5+..+2p-1)=p^{2}=\frac{n^{2}}{4}) si n = 2p+1 }=&space;\Large&space;\sum_{k=1}^{2p+1}{2(k-p-1)x_{k}}=2(p-1)x_{n}+....+2x_{p+2}+2(p-p)x_{p+1}-2x_{p}-...-2(p-1)x_{1}=2p(x_{2p+1}-x_{1})+2(p-1)(x_{2p}-x_{2})+...+2(p-(p-1))(x_{p+2}-x_{p})\leq&space;2(p+(p-1)+...+(p-(p-1)))\leq&space;2p^{2}-(p-1)p=p^{2}+p=\frac{1}{4}(n^{2}-1))
sauf erreur ^^ si ma solution est juste , je n'ai pas d'exo interessant , je laisse quelqu'un d'autre le faire ..... Sylphaen : peut tu expliquer cette partie de ta demonstration? ^_^ - Sylphaen a écrit:
- Solution au problème 57 :
- Spoiler:
-Pour x=0 on a : f(f(y))=f(y)²+f(0) -Pour x=f(z)-f(y) / z £ IR on obtient : f(f(z)-f(y))= ( f(z)-f(y) )² +f(0) Si pour tous x , f(x)=0 alors f est la fonction nul qui réciproquement vérifie les donnés du problème . sinon il existe un réel k t.k f(k) est non nul .
-Pour et a un réel quelconque on obtient :
f(x+f(y))-f(x)=a Donc , dans ce cas ,pour tous réel a il existe 2 réels b,c t.q : a=f(b)-f(c) Alors : f(a)=f(f(b)-f(c))=(f(b)-f(c))²+f(0)=a²+f(0) et réciproquement on vérifie que la fonction f(x)=x²+c est une solution du problème .. Donc les solutions du problème sont la fonction nul et la fonction x->x²+c / c £ IR .
Problème 58 :
x1,x2...,xn ( n>2 ) sont des réel tels que :
Calculer en fonction de n :
est ce qu'on a le droit de dire quepour tous a il existe un x et k tel ke ( ce qui est en rouge) ?? | |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Retour au plaisir :) Sam 18 Déc 2010, 20:30 | |
| Euh si tu remplace x par  et y par k tu trouvera que : f(x+f(y))-f(x)=a | |
|
| | |
just-abdess
Maître
Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
| | Sujet: Re: Retour au plaisir :) Sam 18 Déc 2010, 21:39 | |
| merci c'est claire maintenant (j'ai mal compris les choses) ^_^
Probleme 59 :
Pour quelles valeurs de a et b, entiers superieurs ou égal à 2, (ab-1) est-il divisible par le produit
(a - 1)(b - 1) ? | |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Retour au plaisir :) Dim 19 Déc 2010, 00:41 | |
| Bonsoir : Solution du problème 59 - Spoiler:
(a-1)(b-1) = ab-a-b+1
donc (a-1)(b-1)/(ab-1) = (ab-a-b+1)/(ab-1) = (ab-1-a-b+2)/(ab-1) = 1 - (a+b-2)/(ab-1)
or a et b sont des entier et ab-1 >= 3 donc (a-1)(b-1)/(ab-1) >= 0
et donc les solution sont :
1 - (a+b-2)/(ab-1) =0
ou 1 - (a+b-2)/(ab-1) =1
donc :
a+b-2 = ab-1 ou a+b-2 = 0
or a >= 2 et b >= 2
donc a+b-2 > 0
et pour a+b = ab +1 on a si a et b sont de même parité alors a+b et ab+1 on une parité différente et si a et b on une parité différente alors a+b est impair et ab+1 est pair ce qui est contradictoire dans les deux cas
On conclu que S = ( l'ensemble vide )
Sauf erreur ! Libre à vous de proposé un exercice | |
|
| | |
just-abdess
Maître
Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
| | Sujet: Re: Retour au plaisir :) Dim 19 Déc 2010, 01:23 | |
| ta solution est fausse , tu peux revoir ce qui est en rouge , - darkpseudo a écrit:
- Bonsoir :
Solution du problème 59
- Spoiler:
(a-1)(b-1) = ab-a-b+1
donc (a-1)(b-1)/(ab-1) = (ab-a-b+1)/(ab-1) = (ab-1-a-b+2)/(ab-1) = 1 - (a+b-2)/(ab-1)
or a et b sont des entier et ab-1 >= 3 donc (a-1)(b-1)/(ab-1) >= 0
et donc les solution sont :
1 - (a+b-2)/(ab-1) =0
ou 1 - (a+b-2)/(ab-1) =1 donc :
a+b-2 = ab-1 ou a+b-2 = 0
or a >= 2 et b >= 2
donc a+b-2 > 0
et pour a+b = ab +1 on a si a et b sont de même parité alors a+b et ab+1 on une parité différente et si a et b on une parité différente alors a+b est impair et ab+1 est pair ce qui est contradictoire dans les deux cas
On conclu que S = ( l'ensemble vide )
Sauf erreur !
Libre à vous de proposé un exercice | |
|
| | |
mathslover
Habitué
Nombre de messages : 27
Age : 31
Date d'inscription : 29/10/2009
| | Sujet: Re: Retour au plaisir :) Dim 19 Déc 2010, 09:43 | |
| voici ma solution au bleme 59 : - Spoiler:
(ab-1) est divisible par le produit (a - 1)(b - 1) <=>
il existe un entiers k naturel dans ce cas puique tt est positif :tq :
(ab-1) / (a - 1)(b - 1) = k
<=> (ab-1) / ( ab -a -b + 1 ) = k
<=> (ab -a -b + 1 +a+b-2) / ( ab -a -b + 1 ) = k
<=> (a+b-2) / ( ab -a -b + 1 ) = k-1
<=> (a-1+b-1) / (a - 1)(b - 1) = k' avec k' = (1-k)
<=> 1/(a-1) + 1/(b-1) =k'
on a a >= 2 => 0 < 1/(a-1) =< 1 de meme 0 < 1/(b-1) =< 1
=> 0 < 1/(a-1) + 1/(b-1) =< 2
=> 0 < k' =< 2
donc k'=1 ou k' = 2
<=> (a+b-2) / (a - 1)(b - 1) = 1 ou (a+b-2) / (a - 1)(b - 1) = 2
<=> 2(a+b) -ab-3 = 0 ou 3(a+b)-2ab - 4 = 0
les couples (3,3) pour la premiere equation et (2,2) pour la deuxieme equation sont remarquables. on demontre qu'ils sont les seuls :
pour la premiere equation supposons que:
a#3 et b#3 donc 2(a+b)-3 # 9 et ab # 9 ( on a 9 = 3*3 et 9 = 9*1 et 9=1*9 les deux derniers sont impossibles puisque a>=2 et b>=2 d'où -ab # -9 )
=> 2(a+b) -ab-3 # 0 donc le couple (3,3) est une solution unique de meme pour la deuxieme. alors:
S = { 2, 3 }
 | |
|
| | |
mathslover
Habitué
Nombre de messages : 27
Age : 31
Date d'inscription : 29/10/2009
| | Sujet: Re: Retour au plaisir :) Dim 19 Déc 2010, 20:10 | |
| - Spoiler:
I mean S={ (2,2) et ( 3,3) }
| |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Retour au plaisir :) Dim 19 Déc 2010, 20:35 | |
| - just-abdess a écrit:
- ta solution est fausse , tu peux revoir ce qui est en rouge ,
- darkpseudo a écrit:
- Bonsoir :
Solution du problème 59
- Spoiler:
(a-1)(b-1) = ab-a-b+1
donc (a-1)(b-1)/(ab-1) = (ab-a-b+1)/(ab-1) = (ab-1-a-b+2)/(ab-1) = 1 - (a+b-2)/(ab-1)
or a et b sont des entier et ab-1 >= 3 donc (a-1)(b-1)/(ab-1) >= 0
et donc les solution sont :
1 - (a+b-2)/(ab-1) =0
ou 1 - (a+b-2)/(ab-1) =1 donc :
a+b-2 = ab-1 ou a+b-2 = 0
or a >= 2 et b >= 2
donc a+b-2 > 0
et pour a+b = ab +1 on a si a et b sont de même parité alors a+b et ab+1 on une parité différente et si a et b on une parité différente alors a+b est impair et ab+1 est pair ce qui est contradictoire dans les deux cas
On conclu que S = ( l'ensemble vide )
Sauf erreur !
Libre à vous de proposé un exercice Re sincérement désolé , au fait ce qui est en bleu est juste c'est juste la partie en rouge qu'est une faute ( remarque de toute façon j'ai répondu à la question (ab-1) divise ( a-1)(b-1) Xd normal il faisait nuit et j'avais sommeil ) | |
|
| | |
ayoubmath
Maître
Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
| | Sujet: Re: Retour au plaisir :) Dim 19 Déc 2010, 21:06 | |
| exo soit un rectangle ABCD et un point P tel que  calculer  + 
Dernière édition par ayoubmath le Dim 19 Déc 2010, 21:57, édité 1 fois | |
|
| | |
mathslover
Habitué
Nombre de messages : 27
Age : 31
Date d'inscription : 29/10/2009
| | Sujet: Re: Retour au plaisir :) Dim 19 Déc 2010, 21:48 | |
| au fait, j'attendais juste une confirmation pour poster un nouveau probleme alors qu'un nouveau bleme vient d'être posté ! anyway it's not a prob at all . bonne nuit | |
|
| | |
ayoubmath
Maître
Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
| | Sujet: Re: Retour au plaisir :) Dim 19 Déc 2010, 21:56 | |
| je crois que la dernier exo très dure pour cela je le changer et je laisse pour rechercher
probleme 60
soit ABCD un quadrilatère montrer l'équivalence suivant :
AB+CD=AD+BC <===> ABCD est circonscriptible | |
|
| | |
ayoubmath
Maître
Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
| | Sujet: Re: Retour au plaisir :) Dim 19 Déc 2010, 22:15 | |
| pour premier eq : ABCD est circonscriptible ===> AB+CD=AD+BC est clair  mais pour 2 eq  | |
|
| | |
ayoubmath
Maître
Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
| | Sujet: Re: Retour au plaisir :) Dim 19 Déc 2010, 23:18 | |
|
Dernière édition par ayoubmath le Dim 19 Déc 2010, 23:40, édité 1 fois | |
|
| | |
tarask
Expert sup
Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
| | Sujet: Re: Retour au plaisir :) Dim 19 Déc 2010, 23:28 | |
| Bonsoir ayoub !
S'il te plait , lis bien les règles avant de poster. Quelle sera l'utilité d'un problème si tu le poses et tu y réponds toi même immédiatement ? | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Retour au plaisir :) | |
| |
|
| | |
| | Retour au plaisir :) | |
|
