| | Retour au plaisir :) |  |
|
+33Othmaann MohE Xien ali-mes einstein20 sweet-mounir M.Marjani L'enfant ayoubmath phenix darkpseudo louis supista nmo houssa anas-az_137 stylo vs calculator marouan777 mizmaz Bison_Fûté Mr.Wajih m_zeynep Fermat-X just-abdess mathslover majdouline abdellah=einstein Dijkschneier Sporovitch amazigh-tisffola tarask meryem1994 Sylphaen 37 participants |
|
| Auteur | Message |
|---|
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Lun 20 Déc 2010, 12:48 Lun 20 Déc 2010, 12:48 | |
| s'il nya pas aucune réponse je pose ma solution
POUR NE PAS RETARDER NOTRE JEU
j'attende seulement votre permit | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 09:28 Mar 21 Déc 2010, 09:28 | |
|
pour montrer que : AB+CD=AD+BC ===> ABCD est circonscriptible
((on suppose par l'absurde que ABCD est in-circonscriptible et AB+CD=AD+BC ))
soit T E [CD] tel que ABCT est circonscriptible on a AB+CT=AT+BC
et AB=BC+AD-CD ===> CT+BC+AD-CD=AT+BC ===> CD-CT=AD-AT ===>TD+AT=AD
qui impossible car TD+AT>AD ===> on conclure que ABCD est circonscriptible
| |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 09:42 Mar 21 Déc 2010, 09:42 | |
| problème 61 :soit  et  démontrer que  | |
|
  | |
L'enfant
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 31
Date d'inscription : 11/08/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 11:42 Mar 21 Déc 2010, 11:42 | |
| Ayoub ton premier exo (60) c'était le théoréme de Pitot ...
| |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 20:23 Mar 21 Déc 2010, 20:23 | |
| salut solution 61:- Spoiler:
Application de MA-MG , et MG-MH pour le premier coté :  pour le deuxime coté 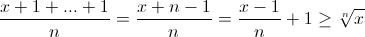 (sauf erreur )
probleme 62:resoudre dans (IN*)^3 l'equation :  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 20:49 Mar 21 Déc 2010, 20:49 | |
| Solution au problème 62 :(y-2)%20\leq%202) * Si y>2 et x > 1, alors x-1 <= 2 et y-2 <= 2, d'où 2 <= x <= 3 et 3<=y<=4. - Si x=2 : L'équation de départ devient équivalente à (4-y)(z+6)=24, ce qui donne les triplets (2,1,2), (2,2,6), (2,3,18). Réciproquement, ces triplets marchent bien. - Si x=3 : L'équation de départ devient équivalente à : (9+2z)(3-y)=27, ce qui donne le triplet (3,2,9), qui réciproquement, marche bien. * Si x=1 : L'équation de départ devient  , ce qui est équivalent à 2z=3y. Réciproquement, on vérifie que tous les triplets (1,y,z) tels que 2z=3y sont des solutions. * Si y=1 et x > 1 : L'équation de départ devient équivalente à (3-z)(x+1)=3, ce qui donne le triplet (2,1,2), qui a déjà été trouvé. * Si y=2 et x > 1 : L'équation de départ devient équivalente à 3x=z. Inversement, les triplets (x,2,z) tels que 3x=z et x > 1 marchent bien. Synthèse : Les triplets solutions sont : (2,1,2), (2,2,6), (2,3,18), (3,2,9), et (1,y,z) tels que 2z=3y, et (x,2,z) tels que 3x=z et x >1.
Dernière édition par Dijkschneier le Mar 21 Déc 2010, 21:21, édité 1 fois | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 21:00 Mar 21 Déc 2010, 21:00 | |
| trés bien , petite remarque : il te manque d'etudier le cas ou y =2 , tu va trouve que (k,2,3k) (k est sup ou egal à 2) est aussi une solution .
A toi maintenant... | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 21:00 Mar 21 Déc 2010, 21:00 | |
| - just-abdess a écrit:
probleme 62:
resoudre dans (IN*)^3 l'equation :
 - Spoiler:
cela équivaut à:2xz+yz=2xy+xyz
si x=1 ==> 2z=3y
on a 2xz+yz>xyz ==> 2x+y>xy ==> y<(2x)/(x-1)=f(x)
or f(x) est une fonction décroissante sur IR
donc si x>3 on aura y<3
il suffira donc de traieter les 4 cas suivants:
y=2 ;y=1 ;x=2;x=3
-si x=2 on aura y<4 et on vérifie à la main y=3;y=2;y=1 ==> z=18,z=6,z=2
-si y=1
on aura : xz+z=3x ==> (x+1)|3 ==> il existe un k tel que x=3k-1 ce qui conduit à (3-z)|1 ==> z=2 ==> x=2
-si y=2 ==> z=3x
-si x=3 on aura y<3 on vérifie à la main y=2 et y=1 on trouve que juste y=2 est solution avec z=9
Puis conclure
sauf erreur bien sur !
@ Dijkschneierdésolé j'étais entrain d'écrire ma solution quand t'as écrit la tienne.
Dernière édition par Sporovitch le Mar 21 Déc 2010, 21:18, édité 1 fois | |
|
  | |
phenix
Féru

 Nombre de messages : 31 Nombre de messages : 31
Age : 30
Localisation : rabat
Date d'inscription : 24/08/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 21:06 Mar 21 Déc 2010, 21:06 | |
| puisque Dijkshneier s'abstient de proposer un problème, je propose un exercice assez facile voilà : Problème 63 :
Trouver un polynome non nul a coefficients entiers tels que : P (racine (2008 ) + racine ( 2009 ) ) = 0  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 21:22 Mar 21 Déc 2010, 21:22 | |
| - just-abdess a écrit:
- trés bien , petite remarque : il te manque d'etudier le cas ou y =2 , tu va trouve que (k,2,3k) (k est sup ou egal à 2) est aussi une solution .
A toi maintenant... Oui, j'ai corrigé. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 21:27 Mar 21 Déc 2010, 21:27 | |
| Solution au problème 63 :On pose :  Par élévation au carré, il vient %20+%202\sqrt{2008%20\times%202009}) , ou encore : %20=%202\sqrt{2008%20\times%202009}) Par une nouvelle élévation au carré, on obtient : )^2%20=%204(2008%20\times%202009)) . Le polynôme %20=%20(x^2%20-%20(2008+2009))^2%20-%204(2008%20\times%202009)) répond au problème. Je n'ai pas de problème à proposer pour le moment. | |
|
  | |
phenix
Féru

 Nombre de messages : 31 Nombre de messages : 31
Age : 30
Localisation : rabat
Date d'inscription : 24/08/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 21:38 Mar 21 Déc 2010, 21:38 | |
| Nice  | |
|
  | |
phenix
Féru

 Nombre de messages : 31 Nombre de messages : 31
Age : 30
Localisation : rabat
Date d'inscription : 24/08/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 21:43 Mar 21 Déc 2010, 21:43 | |
| Problème 64:
Trouver tous les entiers positifs n tels que : (2^n)+3 soit un carré parfait | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 21 Déc 2010, 23:18 Mar 21 Déc 2010, 23:18 | |
| Solution du probleme 64 :- Spoiler:
on va montrer que n=0 est le seul entier tel que 2^n+3 soit un carré parfait
posons que 2^n+3=a^2 , il est claire que a^2 est congru à 1 modulo 3 , donc 2^n est congru à 1 modulo 3 , ce qui donne l'existance d'un b tel que n=2b ,
3=(a-2^b)(a+2^b) donc (a-2^b)=1 et (a+2^b)3 ce qui donne que 2^(b+1)=2
b=0 donc n=0 (sauf erreur)
si ma solution est juste , vous etes libre de poster un nouveau exo ^_^ | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 22 Déc 2010, 12:35 Mer 22 Déc 2010, 12:35 | |
| Solution au problème 64 :Pour n=0, c'est un carré parfait. Pour n=1, ce n'est pas un carré parfait. Soit n>1. Alors on peut poser n = k + 2, tel que k appartienne à N. Par suite : %20+%203) , et ainsi, il est congru à 3 modulo 4. Mais un carré parfait ne peut être congru qu'à 0 ou 1 modulo 4. Synthèse :Le seul n pour lequel 2^n + 3 est un carré parfait est n=0. Problème 65 : (* : une étoile) Est-il possible de paver avec des triminos 3x1 i) Un rectangle 8x8 ? ii) Un rectangle 8x8 auquel manque le coin en haut à gauche ? Merci de ne proposer de réponse que si l'on a la solution à i) et à ii).
Dernière édition par Dijkschneier le Mer 22 Déc 2010, 18:51, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 22 Déc 2010, 18:50 Mer 22 Déc 2010, 18:50 | |
| - phenix a écrit:
- Problème 64:
Trouver tous les entiers positifs n tels que : (2^n)+3 soit un carré parfait Solution 64:- Spoiler:
Soit a un entier vérifiant 2^n+3=a². Pour n=0 2^0+3=a² juste.
Pour tout n£IN* il est évident que a est impair donc 2^n+3=a² <=> 2(2^{n-1}+1)=a²-1=(2k+1)²-1 (k£IN).
Donc 2^{n-1}+1=2k²+2k=2(k²+k) on déduit que n=1 est la seule solution quand n£IN* elle ne vérifie pas l'énoncé. Donc S={1}.
| |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 22 Déc 2010, 19:43 Mer 22 Déc 2010, 19:43 | |
|
salam
pb 64
n=0 -------> 1+3=2²
n=1 -------> 2+3 = n'est pas carré
n> 1
2^n +3 = a² ------> a impair = 2k+1
===> 2^n +3 = 4k²+4k+1
===> 2^(n-1) + 1 = 2k²+2k impossible ( impair = pair)
___________conclusion : n=0.
----------------------------------------------
| |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 22 Déc 2010, 22:32 Mer 22 Déc 2010, 22:32 | |
| - Dijkschneier a écrit:
- Problème 65 : (* : une étoile)
Est-il possible de paver avec des triminos 3x1
i) Un rectangle 8x8 ?
ii) Un rectangle 8x8 auquel manque le coin en haut à gauche ?
Merci de ne proposer de réponse que si l'on a la solution à i) et à ii). Comment ces triminos peuvent étre remis dans l'echequier? Verticalement? Horizontalement? ...? Explique moi. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 22 Déc 2010, 22:55 Mer 22 Déc 2010, 22:55 | |
| N'importe comment. Ou bien verticalement, ou bien horizontalement.  | |
|
  | |
sweet-mounir
Maître
 Nombre de messages : 83 Nombre de messages : 83
Age : 32
Date d'inscription : 16/05/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Jeu 23 Déc 2010, 12:45 Jeu 23 Déc 2010, 12:45 | |
| sluuu les amiis j'aime bien participer avc vous ; j'att l'annonce d'exo | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Sam 25 Déc 2010, 16:21 Sam 25 Déc 2010, 16:21 | |
| Bon après-midi ! Dijkschneier , je crois que le temps dédié à votre exercice s'est écoulé , merci de donner une solution  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Sam 25 Déc 2010, 20:16 Sam 25 Déc 2010, 20:16 | |
| Solution au problème 65 :(i) Une figure pavée entièrement par des triminos 3 × 1 possède un nombre de cases multiple de 3. Or le damier à paver possède un nombre de cases qui n’est pas multiple de 3. La réponse est donc non. (ii) Colorions la deuxième figure avec trois couleurs différentes de la manière suivante :  On remarque qu’un trimino recouvre nécessairement 3 cases dont les couleurs sont deux à deux différentes. Mais la figure à paver ne possède pas la même nombre de cases de chaque couleur, la réponse est donc encore non. Problème 66 : (* : une étoile) Prouver que le nombre a^3 + b^3 + 4 n’est jamais le cube d’un entier pour a et b dans N. | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Dim 26 Déc 2010, 17:42 Dim 26 Déc 2010, 17:42 | |
| Solution probleme 66 :- Spoiler:
un cube d'un entier est toujours congru à 0,1,8 modulo 9 donc a^3+b^3+4 est congru à (4,5,3,2,6) modulo 9 , absurde ....
probleme 67:soient p et q des entiers strictement positifs verifiant :  montrer que 1979 divise p | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Dim 26 Déc 2010, 21:25 Dim 26 Déc 2010, 21:25 | |
| - just-abdess a écrit:
- Solution probleme 66 :
- Spoiler:
un cube d'un entier est toujours congru à 0,1,8 modulo 9 donc a^3+b^3+4 est congru à (4,5,3,2,6) modulo 9 , absurde ....
probleme 67:
soient p et q des entiers strictement positifs verifiant :

montrer que 1979 divise p Alors : =\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{1319}-(\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{659})=\frac{1}{660}+\frac{1}{661}+\frac{1}{662}+...+\frac{1}{1319}=(\frac{1}{660}+\frac{1}{1319})+(\frac{1}{661}+\frac{1}{1318})+...+(\frac{1}{989}+\frac{1}{990})=1979.A) Tel que  Nous savons que 1979 est premier, d'où le résultat. Sauf erreur. | |
|
  | |
phenix
Féru

 Nombre de messages : 31 Nombre de messages : 31
Age : 30
Localisation : rabat
Date d'inscription : 24/08/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Lun 27 Déc 2010, 15:00 Lun 27 Déc 2010, 15:00 | |
| euhhh !!! mizmaz est-ce-que tu peux m'expliquer comment t'as fais pour calculer la dernière somme !! en attendant ta réponse je pose un problème Problème 68 : Prouver qu'il n'existe pas d'entiers n>0 et a_1 <a_2<...<a_n tels que : 1/a1! + 1/a2! +......+ 1/an! = 1/ 10^n   | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  | |
| |
|
  | |
| | Retour au plaisir :) |  |
|
