Retour au plaisir :)

mizmaz a écrit:

just-abdess a écrit:

Solution probleme 66 :

Spoiler:

probleme 67:
soient p et q des entiers strictement positifs verifiant :

montrer que 1979 divise p

Alors :

Tel que
Nous savons que 1979 est premier, d'où le résultat.
Sauf erreur.

Le passage en rouge est érroné, comme si tu veux dire 5=11*(5/11).
On a 5/11 est rationel, donc 11 divise 5, ce qui est clairement faux.
Tu peux essayer autrement.

nmo a écrit:

mizmaz a écrit:

just-abdess a écrit:

Solution probleme 66 :

Spoiler:

probleme 67:
soient p et q des entiers strictement positifs verifiant :

montrer que 1979 divise p

Alors :

Tel que
Nous savons que 1979 est premier, d'où le résultat.
Sauf erreur.

Le passage en rouge est érroné, comme si tu veux dire 5=11*(5/11).
On a 5/11 est rationel, donc 11 divise 5, ce qui est clairement faux.
Tu peux essayer autrement.

LOL. Non, c'est pas faux.

mizmaz a écrit:

LOL. Non, c'est pas faux.

Peux-tu détailler? Quel théorème as-tu utilisé?

nmo a écrit:

mizmaz a écrit:

LOL. Non, c'est pas faux.

Peux-tu détailler? Quel théorème as-tu utilisé?

Le théorème fondamental, vu que le dénominateur, c'est ou un de ses diviseurs et que 1979 ne divise pas cela. Et puis la prochaine fois, essaye d'écrire moins brutalement, ça t'évitera ce genre d'embarras.
Et merci.

mizmaz a écrit:

nmo a écrit:

mizmaz a écrit:

LOL. Non, c'est pas faux.

Peux-tu détailler? Quel théorème as-tu utilisé?

Le théorème fondamental, vu que le dénominateur, c'est ou un de ses diviseurs et que 1979 ne divise pas cela. Et puis la prochaine fois, essaye d'écrire moins brutalement, ça t'évitera ce genre d'embarras.
Et merci.

Je comprends désormais ma faute.

Salut les amis SV avez vou recu les resultats des olymps???

einstein20 a écrit:

Salut les amis SV avez vou recu les resultats des olymps???

Non pas encore et c'est pas l'endroit approprié pour poser cette question (qui est apparemment propre à toi ..)
Gentiment

hhh okey Ds pour le derangement

einstein20 a écrit:

hhh okey Ds pour le derangement

C'est pas grave , mais puisque tu as mis les pieds ici , propose un problème si ça ne dérange pas les autres

okey voila :
Soient a et b deux nombres premeir entre eux dont la somme est un entier impair . prouver que les nombres a+b et a²+b² sont des nombres premiers entre eux.

Il y a déjà ce problème :
Problème 68 :

Prouver qu'il n'existe pas d'entiers n>0 et a_1 <a_2<...<a_n tels que :

1/a1! + 1/a2! +......+ 1/an! = 1/ 10^n

einstein20 a écrit:

okey voila :
Soient a et b deux nombres premeir entre eux dont la somme est un entier impair . prouver que les nombres a+b et a²+b² sont des nombres premiers entre eux.

Merci ! Ma solution dans quelques minutes ...
EDIT:
Petit lemme: si a et b sont premiers entre eux alors ab et a+b le sont aussi .
Preuve:Soit d' divisant ab et a+b ; alors, d' divise a(a+b)-ab=a². On montre de même que d' divise b². Comme a et b sont premiers entre eux, a² et b² sont premiers entre eux. D'où d' ne peut être que 1; ils sont donc premiers entre eux.
Soit d le plus grand commun diviseur de (a+b) et (a²+b²)
alors d divise a+b et d divise a²+b²
on obtient alors d divise 2ab et 2(a+b) , d divise alors 2.PGCD(ab,a+b)=2 alors d=2 ou d=1
si d=2:
on a a+b=2k+1 avec k dans N , donc (a²+b²)= (a+b)²-2ab est impaire , puisque 2=PGCD(a²+b²;a+b) alors 2 divise a²+b² et a+b ce qui est contradictoire .
Conclusion: d=1 alors (a²+b²) et (a+b) sont premiers entre eux .
En attente de confirmation !

mizmaz a écrit:

Il y a déjà ce problème :
Problème 68 :

Prouver qu'il n'existe pas d'entiers n>0 et a_1 <a_2<...<a_n tels que :

1/a1! + 1/a2! +......+ 1/an! = 1/ 10^n

Oui je sais bien mizmaz Et désolé !!

Bon,pour ne pas rester bloqué sur un exo voici un nouveau :

Problème 69 :
Soit (C) un cercle et [AB] un diamètre de (C) .X et Y deux points du même demi-cercle de (C) limité par A et B tels que la distance XY soit constante . Soient C,D les projections orthogonales respectives de X et Y sur (AB) et M le milieu de [XY] .
Montrer que le triangle CMD reste semblable à un triangle fixe


PS : Vous pouvez trouvez la solution du problème 68 sur animath arith prob 70 .

Solution probleme 69 :



on etudie le probleme dans le plan complexe (O,0B,0G) soit Z_1 , Z_2 , Z_c , Z_d , Z_M , des complexes tel qu'il sont les affixes des points X, Y, C,D,M respectivement .

il est clair que :

on a le triangle CMD est isocèle en M . car
on a aussi ..


donc



puisque la longueur XY est fixe donc l'angle theta -alpha est fixe .

donc le le triangle CDM est semblable a un triangle fixe , (le triangle OXY)

probleme 70:

Quel est le nombre de m-uplets ( x_1,x_2,.....,x_m) de (IN*)^m verifiant :
x_1+x_2+....+x_m=n

just-abdess a écrit:

probleme 70:
Quel est le nombre de m-uplets ( x_1,x_2,.....,x_m) de (IN*)^m verifiant :
x_1+x_2+....+x_m=n

Puisqu'il a une relation avec la leçon du dénombrement qu'on vient d'entammer, voici ma solution de cet exercice:
Notons 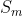le nombre des solutions de cette équation.
Supposons que m=1, l'équation s'écrit .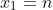
Cette équation est du premier degré.
Donc elle admet une seule solution.
Ainsi .
Supposons que m=2, l'équation s'écrit .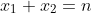
Cette équation équivaut à .
Donc notre équation admet n+1 solutions.
Ainsi .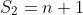
On peut conjecturer que .
Démontrons ce résultat à l'aide d'une récurrence sur l'entier m:
Pour m=1, on a .
Donc .
Le résultat est vrai pour m=1. (Ainsi que pour m=2)
Démonstration de l'hérédité:
Supposons que à un certain rang m et démontrons que la propriété est vraie pour son successeur, c'est à dire que .
Soit l'équation suivante: .
Cette équation équivaut à .
Le nombre de solution de cette équation est donc .
Donc .
Soit .
Ce qui achève le principe de récurrence:
Le nombre de solutions de l'équation proposée est .
(J'ai utilisé à la fin un résultat prouvable aussi avec la récurrence, c'est pour tout entiers n et p vérifiant ).
Sauf erreur d'inattention.

Si ma solution précédant est juste, amusez-vous à résoudre cet exercice:
Problème 71:
Soit ABC un triangle tel que AB=c, BC=a, et CA=b.
Soit r le rayon du cercle circonscrit au triangle ABC.
Démontrez que , et précisez le cas d'égalité.
Bonne chance.

nmo a écrit:

Problème 71:
Soit ABC un triangle tel que AB=c, BC=a, et CA=b.
Soit r le rayon du cercle circonscrit au triangle ABC.
Démontrez que , et précisez le cas d'égalité.
Bonne chance.

Je réponds, puisqu'une semaine s'est écoulée sans aucune tentative:
En guise de simplification, on pose: , , et .
D'une part, selon la loi des sinus appliqué sur ce triangle, on a .
Donc .
Donc , , et .
On a l'inégalité .
Equivaut à .
Donc .==>(*)
(On démontrera cette inégalité, car elle équivaut à la première)
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
La dernière inégalité est toujour valide, elle est donc vraie.
L'inégalité de départ conduit à une inégalité vraie, elle est donc vraie.
Soit .
Ou encore .
P.S: C'est ça ce que j'appelle un exercice d'olympiade.
J'attends des confirmations sur la solution.

Dans l'exercice précédant, l'égalité aura lieu si et seulement si le triangle est équilatéral.
(Cela doit être prouvé) (Il se peut qu'il ait plusieurs cas d'égalité).
Problème 72:
On considère les trinômes du second dégré qui s'écrivent de la forme 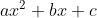tel que .
Trouvez la plus petite valeur de a pour laquelle il existe b et c, de telle sorte que le trinôme admette deux racines distincts appartiennent à l'intervalle ouvert ]0,2[.
Bonne chance.

Solution au problème 72 :
Pour a=1, ce n'est pas possible (voir plus bas).
Pour a=2, c'est possible, et le triplet (2,-3,1) le montre bien.
Cela fait que 2 est la plus petite valeur recherchée.

Supposons que a=1.
Deux racines distinctes, donc b² - 4ac = b² - 4c = Delta > 0, d'où b² > 4c.
x1 et x2, les deux racines, font partie de l'intervalle ouvert ]0,2[ ; donc 0 < -b/a = -b < 4 et 0 < c/a = c < 4 ; d'où : -3<=b<=-1, et 1<=c<=3.
Et compte tenu de b² > 4ac, on se restreint aux 4 cas : -3<=b<=-2 et 1<=c<=2.
Or, aucun de ces 4 cas ne produit deux racines intérieurs à ]0,2[ (je n'ai pas vérifié, mais ça doit être le cas).

Problème 73 : (* : une étoile)
Soit ABCDE un pentagone convexe, et soient M, N, P, Q, X, Y les milieux respectifs des segments BC, CD, DE, EA, MP, NQ.
Montrer que (XY) est parallèle à (AB).

salam

pb 73:

1) Décomposer vect(XY)

2) Utiliser les milieux

3) relation de Chasles

4) aboutir à : vect(XY) = 1/4.vect(BA)

____________________________________________________

Bien houssa. Je m'attendais à une solution qui emploie les nombres complexes, mais ta solution est tout aussi bonne.
J'espère que tu ne m'en voudras pas si je poste un nouveau problème à ta place :
Problème 74 : (* : une étoile)
Soit (C) un cercle de rayon R > 0, et [AB] et [CD] deux cordes de (C) perpendiculaires en M.
Montrer que MA² + MB² + MC² + MD² = 4R².

Ma réponse pour Problème 74:
Soit B' l'intersection du droit passant par B est parallèle avec (CD). On a .
Prenons le triangle ABB' qui est rectangle en B. On a et donc le diamètre AB' est un diamètre de (C) donc on a AB'=2R.
Et on a et donc le trapèze BB'CD est isocèle donc on a BD=B'C.
D'autre part on a AC²+B'C²=AC²+B'C²
Et d'après Pythagore dans le triangle AB'C on a: AC²+B'C²=AB'²=(2R)²=4R²
d'où AC²+BD²=4R²
D'après Pytagore dans le triangle MAC on a: MA²+MC²=AC²
et dans le triangle MBD on a: MB²+MD²=BD²
et puisque AC²+BD²=4R²
alors MA² + MB² + MC² + MD² = 4R²