Retour au plaisir :)

Le problème c'est que tu ne demandais pas au début de trouvé cette borne mais juste de montré qu'elle éxiste , or si dans un ensemble ordonnée il y a un majorant d'un sous ensemble alors ce même sous ensemble accepte bien une borne , quel est cette borne ne nous interesse pas vu que l'énoncé ne le demande pas .

Oui, je suis d'accord que l'énoncé ne demande que de prouver l'existence. Mais il se trouve qu'exhiber cette borne supérieure est le seul moyen (à ma connaissance) de prouver qu'elle existe effectivement.
C'est faux de dire que "si dans un ensemble ordonnée il y a un majorant d'un sous ensemble alors ce même sous ensemble accepte bien une borne" : tu évoques ici la propriété de la borne supérieure, et cette propriété n'est pas vraie dans tout ensemble imaginable comme je l'ai fait remarquer dans mon message précédent.

Dijkschneier a écrit:

Oui, je suis d'accord que l'énoncé ne demande que de prouver l'existence. Mais il se trouve qu'exhiber cette borne supérieure est le seul moyen (à ma connaissance) de prouver qu'elle existe effectivement.
C'est faux de dire que "si dans un ensemble ordonnée il y a un majorant d'un sous ensemble alors ce même sous ensemble accepte bien une borne" : tu évoques ici la propriété de la borne supérieure, et cette propriété n'est pas vraie dans tout ensemble imaginable comme je l'ai fait remarquer dans mon message précédent.

Je n'ai pas vraiment de bonnes bases en domaine d'ensembles, mais je vois mal pourquoi l'existence d'un élément appartenant à un ensemble F et supérieur à tous les éléments d'un sous-ensemble f(A) de F n'implique pas clairement que ce dernier est majoré et donc qu'il admet une borne supérieure dans F. Peux-tu plus m'éclaircir tes idées, s'il te plait ?

Qu'un ensemble soit majoré n'implique pas forcément qu'il admet une borne supérieure.
Je l'ai expliqué dans mes deux derniers messages.

Ok merci pour l'éclaircissement , je me pencherais sur la question quand j'aurais un petit moment , sinon pourrais-tu proposé un nouveau problème pour continué le jeux ?

Je proposerais la solution au problème 85 dans quelques instants.

Solution au problème 85 :
Soit l la borne supérieure de A dans E.
Montrons que f(l) est la borne supérieure de f(A) dans F.
Puisque l est la borne supérieure de A dans E, alors pour tout x de A : x <= l
Par croissante de f, il vient f(x) <= f(l), et par suite, f(l) est un majorant de f(A).
Et donc en particulier, l'ensemble X des majorants de f(A) est non vide.
Soit c un majorant de f(A) tel que c <= f(l).
Puisque c est un élément de F et que f est surjective de E vers F, alors il existe un élément c' de E tel que f(c')=c.
On a donc : f(x) <= f(c') <= f(l), pour tout x de A.
Maintenant, puisque x, c' et l sont des éléments de E, alors par stricte croissante de f dans E, il vient x <= c' <= l, pour tout x de A.
Donc c' majore A et est plus petit ou égal que la borne supérieure de A : donc c'=l.
Par suite : f(c')=f(l), et donc : c=f(l).
f(l) est bien la borne supérieure de f(A).

nmo a écrit:

Problème 83:
Trouvez tous les polynômes satisfaisant .

Après des heures de reflexion et de recherche, voici ce que j'ai trouvé:
Les deux polynômes constants vérifiant la propriété sont et .
Supposons maintenat que P est non constant.
Supposons qu'il existe une racine non nulle k de P.
Pour x=k, on trouve que .
En répétant ce processus, on aura .
Et le polynôme aura une infinité de racine, il est donc le polynôme nul.
Mais puisque P est non constant, donc non nul, on a une contradiction.
On doit donc avoir , car l'ensemble des racines de P est fini.
Par ailleurs, pour x=k+1, on trouve que .
En répétant ce processus, on aura .
Et on aura une contradiction similaire à la précédante.
On aura forcément .
De ce qui précède, on peut affirmer que k est l'une des racines de l'équation dont le discriminent est négatif.
L'équation admet donc deux racines complexes, il s'ensuit que ou que .
On note .
Or, P est à coefficient rééls, si y est racine de P, l'est aussi.
On sait encore que n'importe quel polynôme s'écrit sur la forme où 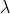est un réél non nul, les sont les racines réélles de P et les sont ses racines complexes de P.
Et par conséquent tel que n est un entier non nul.
On a donc et .
En prenant x=0 dans l'équation de départ, il vient .
Donc soit 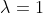ou .
Et si , P serait le polynême nul.
Et cela constitue à nouveau une contradiction.
On conclut ainsi que .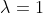
Et finalement tel que n est un entier non nul.
Et réciproquement, soit P un polynôme tel que .
On a .==>(1)
Et .
On a donc soit .==>(2)
De 1 et 2, on conclut que .
Ce qui met fin à la démonstration.
Sauf erreur.

Problème 86:
1-Existe-il des fonctions f et g, tel que ?
2-Trouvez toutes les fonctions f et g, tel que .
Bonne chance.
P.S:Les deux questions sont indépendantes.

Bravo nmo pour ta solution.
Pour qu'il n'y ai pas d"ambiguïtés , tu peux justifier ce passage : On sait encore que n'importe quel polynôme s'écrit sur la forme où est un réel non nul, les sont les racines réelles de P et les sont ses racines complexes de P.

Et aussi : De ce qui précède, on peut affirmer que k est l'une des racines de l'équation .

Merci!

La solution de nmo est du genre typique pour ce genre de problèmes voir le marathon des oraux d'algèbre le 1 er exercice ici: https://mathsmaroc.jeun.fr/t18127-marathon-d-oraux

Oui oui , tu te doutes bien que je sais pourquoi , c'est du cours en prépa ...
C'est juste pour permettre à nmo de savoir pourquoi tout polynômes sur C est scindé

nmo a écrit:

Problème 86:
1-Existe-il des fonctions f et g, tel que ?
2-Trouvez toutes les fonctions f et g, tel que .
Bonne chance.
P.S:Les deux questions sont indépendantes.

Voici une réponse:
1-La réponse est oui, on peut l'illustrer par un exemple:
Soit g une fonction définie ainsi: .
On définit la fonction f de telle sorte que , une fois qu'on ait .
Il est clair que .
On démontre maintenat que ces deux fonction constituent bel et bien une réponse:
*On a tout d'abord .==>(1)
*On a aussi:
.
D'où: .==>(2)
De 1 et 2, on conclût.
2-On a .
Donc , soit .
Soit un réél qui vérifie .
On a .
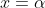Pour , il vient .
Et cela implique que , soit .
Ce qui s'écrit encore .
Ainsi, il existe deux rééls différents et de tel que .
Mais, on a d'après l'hypothèse: et .
Et puisque , on aura .
Ainsi , ou encore .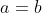
Et cela constitue une contradiction.
Les fonctions qu'on cherche à trouver n'existent pas par conséquent.
Sauf erreur.

Je propose un nouveau problème:
Problème 87:
Démontrez que pour n'importe quel entier n supérieur ou égal à 3, il existe deux entiers naturels impairs x et y tels que: .
Bonne chance.

nmo a écrit:

Je propose un nouveau problème:
Problème 87:
Démontrez que pour n'importe quel entier n supérieur ou égal à 3, il existe deux entiers naturels impairs x et y tels que: .
Bonne chance.

Je propose une solution:
On raisonne par récurrence sur l'entier n:
-Initialisation:
Pour n=3, on a: .
Donc la propriété est valide pour le petit indice 3.
-Hérédité:
Supposons que la propriété est vrai pour un certain indice n, et démontrons qu'elle l'est également au rang n+1.
C'est à dire, on suppose que: .
Et on doit prouver que: .
On a:
.
Et puisque x et y sont des entiers impairs, il vient que .
Il s'ensuit que:
.
On distingue deux cas:
*Cas 1: a et b sont de la même parité.
On aura donc a+7b+4 et a-b deux entiers pairs, et a-7b-3 et a+b+1 deux entiers impairs.
Ainsi: .
*Cas 2: a et b sont de parité différente.
On aura donc a+7b+4 et a-b deux entiers impairs, et a-7b-3 et a+b+1 deux entiers pairs.
Ainsi .
*Conclusion:
Dans les deux cas, on affirme que la propriété est valide pour n+1.
-Conclusion de la récurrence:
(x et y étant impairs).
CQFD.
Sauf erreur.

nmo a écrit:

nmo a écrit:

Je propose un nouveau problème:
Problème 87:
Démontrez que pour n'importe quel entier n supérieur ou égal à 3, il existe deux entiers naturels impairs x et y tels que: .
Bonne chance.

Je propose une solution:
On raisonne par récurrence sur l'entier n:
-Initialisation:
Pour n=3, on a: .
Donc la propriété est valide pour le petit indice 3.
-Hérédité:
Supposons que la propriété est vrai pour un certain indice n, et démontrons qu'elle l'est également au rang n+1.
C'est à dire, on suppose que: .
Et on doit prouver que: .
On a:
.
Et puisque x et y sont des entiers impairs, il vient que .
Il s'ensuit que:
.
On distingue deux cas:
*Cas 1: a et b sont de la même parité.
On aura donc a+7b+4 et a-b deux entiers pairs, et a-7b-3 et a+b+1 deux entiers impairs.
Ainsi: .
*Cas 2: a et b sont de parité différente.
On aura donc a+7b+4 et a-b deux entiers impairs, et a-7b-3 et a+b+1 deux entiers pairs.
Ainsi .
*Conclusion:
Dans les deux cas, on affirme que la propriété est valide pour n+1.
-Conclusion de la récurrence:
(x et y étant impairs).
CQFD.
Sauf erreur.

Trés bien. J'aime la démarche.

cette solution est extrait d'un site marocain de mathématiques.

geom a écrit:

cette solution est extrait d'un site marocain de mathématiques.

D'où exactement?
La récurrence me semble l'outil parfait de résolution de ce problème.
De plus, c'est tiré de l'olympiade de la bulgarie.

geom a écrit:

nmo a écrit:

geom a écrit:

cette solution est extrait d'un site marocain de mathématiques.

D'où exactement?

http://adnane.megabyet.net/ > تمارين أولمبياد محلولة

Elle ressemble à ma solution au début, et elle n'est pas détaillée vers la fin.
Problème 88:
ABCD est un quadilatère inscrit dans le cercle de diamètre [AC].
Soient E et F les projections orthogonales de C et A respectivement sur (BD).
Démontrez que: BE=DF.
Bonne chance.

nmo a écrit:

Problème 88:
ABCD est un quadilatère inscrit dans le cercle de diamètre [AC].
Soient E et F les projections orthogonales de C et A respectivement sur (BD).
Démontrez que: BE=DF.
Bonne chance.

D'aprés la théorème de Pythagore dans les triangles et et et respectivement on a:




et on [AC] un diamètre alors:
et on a et alors et puisque alors

Solution alternative pour problème 88:


Soit O le centre du cercle circonscrit au quadrilatère ABCD.

On note X la projection orthogonale de O sur (BD).

On considère l'application P qui associe chaque point M par le point M' tel que M' est la projection orthogonale de M sur (BD).

On a: P(A)=F et P(C)=E et P(O)=X, et on a O le milieu de [AC], et puisque la projection orthogonale est une transformation du plan qui conserve les barycentres, on conclut que: X est le milieu de [EF], alors: XE=XF.

Et on a OB=OD et donc (OX) est la médiatrice du segment [BD].

Et puisque: , alors: XD=XB.

Et on a: BE=BF+FX+XE=ED+FX+XE=DF.

D'où le résultat voulut.

geom a écrit:

nmo a écrit:

Problème 88:
ABCD est un quadilatère inscrit dans le cercle de diamètre [AC].
Soient E et F les projections orthogonales de C et A respectivement sur (BD).
Démontrez que: BE=DF.
Bonne chance.

D'aprés la théorème de Pythagore dans les triangles et et et respectivement on a:




et on [AC] un diamètre alors:
et on a et alors et puisque alors

Il ya une autre méthode plus belle on utilisons les triangles semblables et chasse d'angle

est ce que mon méthode est vrai?

geom a écrit:

nmo a écrit:

Problème 88:
ABCD est un quadilatère inscrit dans le cercle de diamètre [AC].
Soient E et F les projections orthogonales de C et A respectivement sur (BD).
Démontrez que: BE=DF.
Bonne chance.

D'aprés la théorème de Pythagore dans les triangles et et et respectivement on a:




et on [AC] un diamètre alors:
et on a et alors et puisque alors

Tu as inversé les rôles de E et F !

La prochaine fois, tu aurais au moins lire le problème.