Retour au plaisir :)

Solution Problème 74 :

Selon Mr. Pythagore : MA²+MB²+MC²+MD² = AD²+CB²
et aussi Mr. Al-Kashi : AD²=2R²+2R²cos(AOD) et CB²=2R²+2R²cos(COB)
=> AD²+CB² = 4R² + 2R²(cos(AOD)+cos(COB)) (*)

Nous avons aussi : AOD=2ABD et COB=2BDC et ABD=MBD=pi/2-BDM (BMD triangle rectangle en M )
alors AOD = pi - 2BDM = pi - COB

=> cos(AOD)=cos(pi-COB)=-cos(COB)
(*) => AD²+CB²=4R²
<=> MA² + MB² + MC² + MD² = 4R²

Je vous présente cet exo:

Problème 75:
Montrer que si x+y+z=6 et xy+yz+xz=9 alors x, y et z appartient à [0,4].

Dijkschneier a écrit:

Solution au problème 72 :
Pour a=1, ce n'est pas possible (voir plus bas).
Pour a=2, c'est possible, et le triplet (2,-3,1) le montre bien.
Cela fait que 2 est la plus petite valeur recherchée.
Supposons que a=1.
Deux racines distinctes, donc b² - 4ac = b² - 4c = Delta > 0, d'où b² > 4c.
x1 et x2, les deux racines, font partie de l'intervalle ouvert ]0,2[ ; donc 0 < -b/a = -b < 4 et 0 < c/a = c < 4 ; d'où : -3<=b<=-1, et 1<=c<=3.
Et compte tenu de b² > 4ac, on se restreint aux 4 cas : -3<=b<=-2 et 1<=c<=2.
Or, aucun de ces 4 cas ne produit deux racines intérieurs à ]0,2[ (je n'ai pas vérifié, mais ça doit être le cas).

Ce n'est pas la bonne methode, par exemple si tu avais les racines à l'intérieur de ]0,1[, tu allais chercher plusieurs cas afin d'aboutir à a=5.
D'où l'utilité d'une solution plus rigoureuse.
Voici la solution approprié:
Soit 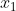et 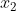les racines du polynôme P.
On écrit donc .==>(*)
Remarquons que 0 et 2 ne font pas parties des racines du polynôme.
Le signe du polynôme entre les racines est négatif, car a est positif puisqu'il est entier.
Ainsi en dehors, des racines le polynôme a un signe positif.
D'ou P(0) et P(2) sont positifs.
Donc .
Et puisque P(2) et P(0) sont des entiers relatifs, il vient que .
En utilisant *, il s'ensuit que .
Donc .==>(1)
D'un autre côté, la fonction admet un maximum, qui n'est autre que 1.
On a .
Donc et .
Soit et .
Donc .
Avec égalité si et selemet si .
Mais puisque les racines sont distincts, on écrit .
Donc .
En utilisant 1, .
Donc , car a est un entier.
Et finalement 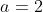est la valeur recherchée.
Le polynôme est une illustration merveille de la réponse.
Au plaisir.
Sauf erreur.

@nmo : je crois que ta solution n'est pas forcément la plus bonne : il suffit peut-être de changer un peu les paramètres de l'énoncé pour qu'elle devienne inapplicable...
Solution au problème 75 :
xy+yz+xz = 9
<=> x(y+z) + yz = 9
<=> (6-(y+z))(y+z) + yz = 9
<=> yz = (y+z)² - 6(y+z) + 9
Or, pour tous réels y et z, on a la majoration : yz <= (y+z)²/4
Donc en posant X = y+z, il vient que :
4(X² - 6X + 9) <= X²
=> 3X² - 24X + 36 <= 0
=> 2 <= X <= 6
=> 2 <= 6 - x <= 6
=> 0 <= x <= 4
Et on obtient évidemment les mêmes encadrements pour y et z, puisque la situation est symétrique.

Dijkschneier a écrit:

@nmo : je crois que ta solution n'est pas forcément la plus bonne : il suffit peut-être de changer un peu les paramètres de l'énoncé pour qu'elle devienne inapplicable...

Pour me convaicre, donne moi une situation de la sorte.

Lorsque tu dis par exemple que :

Citation :

a > 1
Donc a>=2, car a est un entier.
Et finalement a=2 est la valeur recherchée.

En toute rigueur, cette conclusion est fausse. a>=2 n'implique pas que 2 est le minimum : il faut encore et toujours trouver un exemple d'un polynôme satisfaisant pour a=2.
Car tu es parti en implications...
Et donc on peut imaginer des situations où on trouve dans notre analyse que a > 5, mais où le minimum est en fait 100000...

Problème 76 : (** : deux étoiles)
Montrer qu'un triangle ABC est rectangle si et seulement si son cercle circonscrit et son cercle d'Euler sont tangents.

Dijkschneier a écrit:

Lorsque tu dis par exemple que :

Citation :

a > 1
Donc a>=2, car a est un entier.
Et finalement a=2 est la valeur recherchée.

En toute rigueur, cette conclusion est fausse. a>=2 n'implique pas que 2 est le minimum : il faut encore et toujours trouver un exemple d'un polynôme satisfaisant pour a=2.
Car tu es parti en implications...
Et donc on peut imaginer des situations où on trouve dans notre analyse que a > 5, mais où le minimum est en fait 100000...

Je n'ai pas fait attention à ce point.
Je comprends très bien ma faute.

Dijkschneier a écrit:

Problème 76 : (** : deux étoiles)
Montrer qu'un triangle ABC est rectangle si et seulement si son cercle circonscrit et son cercle d'Euler sont tangents.

bonsoir!!
je pense que c'est facil car on sait que :
deux cercles de centres O1 et O2, de rayons r1 et r2 tels que r1 > r2 sont tangents intérieurement si et seulement si O1O2 = r1 - r2.

on prend: O le centre du cercle circonscrit et O' le centre du cercle d'euler.r et r' les rayons des deux cercle
dans ce probleme il suffit de demontrer que OO'=AO-O'A ce qui est clairement juste (tout est clair avec un dessin).

marouan777 a écrit:

bonsoir!!
je pense que c'est facil car on sait que :
deux cercles de centres O1 et O2, de rayons r1 et r2 tels que r1 > r2 sont tangents intérieurement si et seulement si O1O2 = r1 - r2.

on prend: O le centre du cercle circonscrit et O' le centre du cercle d'euler.r et r' les rayons des deux cercle
dans ce probleme il suffit de demontrer que OO'=AO-O'A ce qui est clairement juste (tout est clair avec un dessin).

r' = O'A ??!
Le cercle d'Euler d'un triangle ne passe pas par les sommets du triangle.

le pieds de hauteur issue de a H ......H=h(a)

D'accord.
Alors je te demanderais de démontrer que OO'=AO-O'h(A) puisque c'est quand même le problème.

aah oui il une equivalence ..... att j'ai pas pris attention.....je cherche encore...

on a :OO'=AO-O'h(a) <=>OO'=r-(r/2) <=>2OO'=r<=>OH=r <=> OA=OH et OH=OB et OB=OH et cela n'est juste que dans un triangle rectangle.

Bien.

bonsoir!!
desolé j'ai pas d'exrcice a vous proposer...chaqu'un se sente libre de poster un.......

Voici un nouvel problème:
Problème 77:
Soit un cercle de centre O.
Soit A, B, C, et D quatres points de ce cercle.
Soient I, J, K, et L les milieux respectifs de AB, BC, CD, et DA. I', J', K', et L' les projections orthogonales respectives de I, J, K, et L sur les droites (CD), (DA), (AB), et (BC).
Montrez que les quatres droites (II'), (JJ'), (KK'), et (LL') sont concourantes.
Bonne chance.

Solution au problème 78 :
Considérons O comme étant l'origine du plan complexe.
Dénotons par une lettre minuscule l'affixe d'un point en majuscule.
Soit O9 le centre du cercle d'Euler du quadrilatère ABCD (o9 = (a+b+c+d)/2).
Nous allons montrer que les droites sont concourantes en O9.
On a :
i = (a+b)/2
j = (b+c)/2
k = (c+d)/2
l = (a+d)/2
(II') : (z-i).(d-c) = 0
(JJ') : (z-j).(b-c) = 0
(KK') : (z-k).(d-c) = 0
(LL') : (z-l).(a-d) = 0
où le point . désigne le produit réel (real product ou dot product) défini comme suit : a.b = 1/2 (conjugué(a) b + a conjugué(b))
On remarque alors que o9 = (a+b+c+d)/2 appartient à toutes ces droites, car il vérifie leurs équations : on a par exemple :
( (a+b+c+d)/2 - (a+b)/2 ).(d-c) = 0
<=> (c+d).(d-c) = 0
<=> c.d - c.c + d.d - d.c = 0
<=> d.d - c.c + c.d - c.d = 0 (ce produit est commutatif)
<=> d.d = c.c
<=> |d|² = |c|²
<=> OD² = OC²
Ce qui est vrai, puisque A,B,C et D sont cocycliques et O est le centre du cercle...

Essayez d'éviter les solutions intervenants les complexes, les calcules en générale. Pour une solution synthetique, Pensez à completer des parallelogrammes comme OIO'K.

Je propose encore ces deux exercices:
Problème 79:
Prouvez que .
Problème 80:
Résolvez en IR l'équation suivante .
Où désigne la partie décimale de x et la partie entière de x.
Bonne chance.

Salut Mohe !
Pourquoi éviter les complexes alors que c'est un outil puissant ?

C'était le conseil des correcteures à Rabat. Ils disaient que c'est innacceptable à l'IMO. A mon avis ils ont raison, Il faut toujours créer et immaginer, surtout lorsqu'il s'agit de la Géometrie, sinon je trouve que ca ne fais aucun problème de risquer pour trouver une solution synthetique puisque ça vaut un prix spécial!

Solution au problème 80 :
Posons x=p+r tels que p = E(x) et r={x}.

Considérons cette dernière équation comme une équation du second degré en r.

Étant donné que 0<=r<1, on en déduit que .
=>
=>
=>
=>
=> p=0 ou p=1 ou p=2 ou p=3 ou p=4
Il ne reste plus qu'à faire une étude de cas...
p=0 est impossible car p est un dénominateur dans l'expression initiale.
Je n'ai pas envie de faire les autres cas pour le moment.

@Mohe : je ne pense pas que c'est inacceptable. Ce n'est pas apprécié, mais ce n'est pas refusé !! La méthode des multiplicateurs de Lagrange, qui est une méthode calculatoire extrêmement puissante pour résoudre des problèmes d'optimisation (inégalités), est acceptée à l'IMO (sous condition de faire les calculs juste), mais n'est pas appréciée.
Arnav Tripathy en parle vers la fin ici : https://www.youtube.com/watch?v=3tpDqliD6Ss

Solution au problème 79 :

=

=

=

On en conclut.
Autrement, on peut écrire 100! / (50!)² = (100/50 . 99/49 . 98/49 . 97/48 ... 7/3 . 6/3 . 5/2 . 4/2 . 3 . 2)/50 > (2 . 2 . 2 ... 2 . 7/3 . 2 . 5/2 . 2 . 3 . 2)/50 , et arriver ainsi à montrer le côté gauche.
Et on fait presque la même chose pour le côté droit.
Mais tout cela reste bien sûr calculatoire.