| | Applications de l'inégalité de Karamata |  |
|
+4Syba boubou math Oty bel_jad5 8 participants |
|
| Auteur | Message |
|---|
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Applications de l'inégalité de Karamata Sujet: Applications de l'inégalité de Karamata  Ven 02 Nov 2012, 22:23 Ven 02 Nov 2012, 22:23 | |
| Ce lien est réservé à l'inégalité de Karamata, elle est facile à comprendre et terriblement efficace. Celui qui résout l'exercice devra proposer un nouveau dans cette page et ainsi de suite.
http://en.wikipedia.org/wiki/Karamata%27s_inequality
Je commence: soient a,b,c des réels strictement positifs. montrer que:
1/(a+b)+1/(b+c)+1/(a+c) <= 1/(2a)+1/(2b)+1/(2c)
Dernière édition par bel_jad5 le Ven 02 Nov 2012, 22:39, édité 1 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Ven 02 Nov 2012, 22:35 Ven 02 Nov 2012, 22:35 | |
| qu'est ce que l'inégalité Karamata ? Merci beaucoup , sinon pour cette inégalité voici ma solution : Par C-S : }\leq&space;\frac{1}{2b}+\frac{1}{2c}) il suffit de sommer cycliquement | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Ven 02 Nov 2012, 22:40 Ven 02 Nov 2012, 22:40 | |
| J'ai ajouté le lien vers l'inégalité. Ta solution est bonne mais elle ne répond pas aux contraintes de l'exercice  | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Sam 03 Nov 2012, 21:39 Sam 03 Nov 2012, 21:39 | |
| Pour ceux qui ne la connaissent pas, essayez d apprendre cette technique aussi!  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Sam 03 Nov 2012, 22:27 Sam 03 Nov 2012, 22:27 | |
| Solution par symétrie ,supposons que 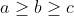 on ainsi :  ainsi (2a,2b,2c) majore (a+b,b+c,a+c) En tenant compte du fait que la fonction f(x)=1/x est convexe ,et on utilisant l'inégalité de karamata ,on obtient : +f(2b)+f(2c)\geq&space;f(a+b)+f(b+c)+f(a+c)\Leftrightarrow&space;\frac{1}{2a}+\frac{1}{2b}+\frac{1}{2c}\geq&space;\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}) j'avais déjà entendu parler de cette inégalité mais à vrai dire je ne la connaissais pas  . la méthode de oty reste la meilleure à mon avis vue la simplicité ,j'aimerais bien trouver un exemple dans le quel cette inégalité devient indispensable .
Dernière édition par boubou math le Dim 04 Nov 2012, 10:29, édité 1 fois | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Sam 03 Nov 2012, 22:40 Sam 03 Nov 2012, 22:40 | |
| Solution juste. Je propose un nouveau exercice alors.
Inegalite 2: IMO 2000
Soient a,b,c des reels positifs tels que: abc = 1.
Montrer que: (a-1+1/b)(b-1+1/c)(c-1+1/a)<=1
Indication:
1) d abord eliminer la contrainte abc=1 en introduisant de nouvelles variables x,y,z...
2) consider la fonction -ln(x) (attention au cas ou x<0 )
...
Dernière édition par bel_jad5 le Sam 03 Nov 2012, 23:58, édité 1 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Sam 03 Nov 2012, 22:56 Sam 03 Nov 2012, 22:56 | |
| Mr Bel_Jad , je crois que c'est a vous qu'on doit remettre la responsabilité de la préparation des equipes marocaine , vraiment tbarkellah 3like , vous avez une expérience au IMO et vous avez partagez vos connaissances BRAVO !
Ps : je pense que cette Karamata est interdite au IMO ,
sinon il faut la prouver avant de l'utiliser ce qui est vraiment tres difficile et pas efficace .
je crois que seul les inégalités de BASES comme C-S , AM-GM , chebychev .... qui sont permis . Merci . | |
|
  | |
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Sam 03 Nov 2012, 23:24 Sam 03 Nov 2012, 23:24 | |
| On pose: a=x/y , b=y/z , c=z/x (x,y,z strictement positifs)
(a-1+1/b)(b-1+1/c)(c-1+1/a)<=1
<=>(x-y+z)(y-z+x)(z-x+y)<=xyz
On suppose que: x<=y<=z
x>(x+y-z)
x+y>(x+y-z)+(z+x-y)
x+y+z=(x+y-z)+(z+x-y)+(z+y-x)
On considère la fonction f(x)=-ln(x) qui est convexe biensur.
f(x)+f(y)+f(z)<=f(x+y+z)+f(z+x-y)+f(z+y-x)
Le résultat en découle. | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Sam 03 Nov 2012, 23:45 Sam 03 Nov 2012, 23:45 | |
| Il y a une petite erreur "non triviale" dans ton raisonnement. Tu as utilisé la fonction -ln(x) alors il faut que x soit strictement positif. Donc tu fais une étude de cas: x+y-z<=0 alors il n y a rien à montrer puisque (x-y+z)(y-z+x)(z-x+y)<=0<=xyz x+y-z>0 alors là tu utilises Karamata. Mais généralement, très bonne solution  | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Sam 03 Nov 2012, 23:45 Sam 03 Nov 2012, 23:45 | |
| Oty: merci pour le compliment  | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Sam 03 Nov 2012, 23:47 Sam 03 Nov 2012, 23:47 | |
| - Oty a écrit:
- Mr Bel_Jad , je crois que c'est a vous qu'on doit remettre la responsabilité de la préparation des equipes marocaine , vraiment tbarkellah 3like , vous avez une expérience au IMO et vous avez partagez vos connaissances BRAVO !
Ps : je pense que cette Karamata est interdite au IMO ,
sinon il faut la prouver avant de l'utiliser ce qui est vraiment tres difficile et pas efficace .
je crois que seul les inégalités de BASES comme C-S , AM-GM , chebychev .... qui sont permis . Merci . T'es sur Othmane :O si oui j'aimerais Bien que tu me passe une source | |
|
  | |
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Sam 03 Nov 2012, 23:48 Sam 03 Nov 2012, 23:48 | |
| Ah merci pour la remarque, j'ai pas fait attention ^^ | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Sam 03 Nov 2012, 23:57 Sam 03 Nov 2012, 23:57 | |
| Inégalité 3: Asian Pacific Olympid 1996
Soient a,b,c les côtés d'un triangle. montrer que:
rac(a+b-c)+rac(b+c-a)+rac(c+a-b)<=rac(a)+rac(b)+rac(c) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Dim 04 Nov 2012, 00:00 Dim 04 Nov 2012, 00:00 | |
| - alidos a écrit:
T'es sur Othmane :O si oui j'aimerais Bien que tu me passe une source je tiens cette information d'un ami sur AOPS , aussi si c'est methode etait permise alors elles seraient étudier dans Les stages , or ce n'est pas le cas . | |
|
  | |
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Dim 04 Nov 2012, 00:08 Dim 04 Nov 2012, 00:08 | |
| On suppose que: a>=b>=c (a,b,c tous strictement positifs)
Alors:
(a+b-c)>=a
(a+b-c)+(a+c-b)>=a+b
(a+b-c)+(a+c-b)+(b+c-a)=(a+b+c)
On considère la fonction f(x)=rac(x) définie sur R+, qui est concave biensur sur R*+.
Donc on a:
rac(a+b-c)+rac(a+c-b)+rac(b+c-a)<=rac(a)+rac(b)+rac(c)
(Le cas d'égalité si: a=b=c)
D'ou le résultat. | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Dim 04 Nov 2012, 00:16 Dim 04 Nov 2012, 00:16 | |
| Jolie. Je vois que tu as maitrisé la technique  | |
|
  | |
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Dim 04 Nov 2012, 00:19 Dim 04 Nov 2012, 00:19 | |
| | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Dim 04 Nov 2012, 00:21 Dim 04 Nov 2012, 00:21 | |
| Inégalité 4:
Soient a(1), a(2), a(3),...,a(2n+1) des réels strictement positifs tels que a(1)>=a(2)>= a(3)>=...>=a(2n+1)>= 0. Et soit f une fonction convexe de [0,a(1)] vers R. montrer que:
f(a(1)-a(2)+a(3)-...+a(2n+1))<=f(a(1))-f(a(2))+f(a(3))-.....+f(a(2n+1)) | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Dim 04 Nov 2012, 10:26 Dim 04 Nov 2012, 10:26 | |
| - boubou math a écrit:
- Solution
par symétrie ,supposons que
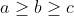
on ainsi :

ainsi (a,b,c) majore (a+b,b+c,a+c)
En tenant compte du fait que la fonction f(x)=1/x est convexe ,et on utilisant l'inégalité de karamata ,on obtient :
+f(2b)+f(2c)\geq&space;f(a+b)+f(b+c)+f(a+c)\Leftrightarrow&space;\frac{1}{2a}+\frac{1}{2b}+\frac{1}{2c}\geq&space;\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c})
j'avais déjà entendu parler de cette inégalité mais à vrai dire je ne la connaissais pas  . .
la méthode de oty reste la meilleure à mon avis vue la simplicité ,j'aimerais bien trouver un exemple dans le quel cette inégalité devient indispensable .
on doit ecrire (2a,2b,2c) majore (a+b,b+c,a+c) | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Dim 04 Nov 2012, 10:29 Dim 04 Nov 2012, 10:29 | |
| - younesmath2012 a écrit:
- boubou math a écrit:
- Solution
par symétrie ,supposons que
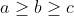
on ainsi :

ainsi (a,b,c) majore (a+b,b+c,a+c)
En tenant compte du fait que la fonction f(x)=1/x est convexe ,et on utilisant l'inégalité de karamata ,on obtient :
+f(2b)+f(2c)\geq&space;f(a+b)+f(b+c)+f(a+c)\Leftrightarrow&space;\frac{1}{2a}+\frac{1}{2b}+\frac{1}{2c}\geq&space;\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c})
j'avais déjà entendu parler de cette inégalité mais à vrai dire je ne la connaissais pas  . .
la méthode de oty reste la meilleure à mon avis vue la simplicité ,j'aimerais bien trouver un exemple dans le quel cette inégalité devient indispensable .
on doit ecrire (2a,2b,2c) majore (a+b,b+c,a+c) oué faute d'inattention . | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 | |
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Dim 04 Nov 2012, 20:34 Dim 04 Nov 2012, 20:34 | |
| qu'est ce que vous disez Mr"bel_jad5" ? | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Dim 04 Nov 2012, 22:04 Dim 04 Nov 2012, 22:04 | |
| | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Dim 04 Nov 2012, 22:36 Dim 04 Nov 2012, 22:36 | |
| non , mais il manque un peu d'ennoncé pour demmarer avec Karamata !!! et je suis sur qu'on va utiliser ce que j'ai ecrit : ~~majore~~la~~suite~~\left%20(%20a_{1};a_{3};a_{5};...;a_{2n+1}%20\right%20)}\\dans~~ce~~cas:~~on~~aura~~directement~~le~~resultat%20~~!!!) | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  Dim 04 Nov 2012, 22:54 Dim 04 Nov 2012, 22:54 | |
| peux tu rédiger ton raisonnement proprement ? | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Applications de l'inégalité de Karamata Sujet: Re: Applications de l'inégalité de Karamata  | |
| |
|
  | |
| | Applications de l'inégalité de Karamata |  |
|
