Applications de l'inégalité de Jensen(Convexité)

Ce lien est réservé à l'inégalité de Jensen (convexité). Celui qui résout l'exercice devra proposer un nouveau dans cette page et ainsi de suite.

http://fr.wikipedia.org/wiki/In%C3%A9galit%C3%A9_de_Jensen

Inégalité 1:
Je commence: soient a,b,c des réels strictement positifs. montrer que:

a²/(a+b)+b²/(b+c)+c²/(c+a)>=(a+b+c)/2

à vous de jouer

bel_jad5 a écrit:

Ce lien est réservé à l'inégalité de Jensen (convexité). Celui qui résout l'exercice devra proposer un nouveau dans cette page et ainsi de suite.
http://fr.wikipedia.org/wiki/In%C3%A9galit%C3%A9_de_Jensen
Je commence: soient a,b,c des réels strictement positifs. montrer que:
a²/(a+b)+b²/(b+c)+c²/(c+a)>=(a+b+c)/2
à vous de jouer

Voici ce que j'ai fait:
L'inégalité s'écrit: , où .
Où: , et .
Donc la deuxième dérivée de la fonction f est strictement positive sur l'intervalle [[, f est donc convexe.
On applique l'inégalité de la convexité:
On aura: .
Ce qui met fin à la démonstration.

L'inégalité 2:
Soit , et des réels strictement positifs vérifiant l'identité .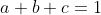
Montrez que: .
Bonne chance.

NMO: Jolie demonstration

bel_jad5 a écrit:

Ce lien est réservé à l'inégalité de Jensen (convexité). Celui qui résout l'exercice devra proposer un nouveau dans cette page et ainsi de suite.

http://fr.wikipedia.org/wiki/In%C3%A9galit%C3%A9_de_Jensen

Inégalité 1:
Je commence: soient a,b,c des réels strictement positifs. montrer que:

a²/(a+b)+b²/(b+c)+c²/(c+a)>=(a+b+c)/2

à vous de jouer

Caushy

Salam Amine,

Jolie demonstration aussi mais le but de ces liens est de pratiquer les techniques d olympiades. Donc, a la place de resoudre des exercices de facons aleatoires, je prefere qu on se focalise sur les techniques. Ta demonstration est bonne mais elle n est adaptee a ce lien.

Essayes de resoudre l exercice de "nmo" en utilisant la convexite...

nmo a écrit:

L'inégalité 2:
Soit , et des réels strictement positifs vérifiant l'identité .
Montrez que: .
Bonne chance.

j'ai une solution mais pas avec Jensen :
on pose on a
avec
et puisque :
donc

Essayes de le faire avec Jensen. C est le BUT

Si tu arrives pas, voila une petite indication: la fonction "Racine" est concave ...

oui je sais
voici la 2eme méthode :

on pose donc
=> f est concave
apr jensen

Je donne une solution detaillee qui aidera les autres a comprendre la technique.

1) on voit que l inegalite s ecrit comme w*Racine(y) donc on a envie de considerer la fonction racine et w comme poids.

2) si les coefficients n ont pas une somme egale a 1 alors il suffit de les diviser par leur somme. Ici dans l exercice, on a pas besoin de faire ca puisque a+b+c = 1

3) la fonction racine est concave alors l inegalite est de le sens oppose, c a d:
af(b)+bf(c)+cf(a)<=f(a*b+b*c+c*a)

4) on developpe:
a*racine(b)+b*racine(c)+c*racine(a)<=racine(ab+bc+ac)<=racine((a+b+c)^2/3) = racine(3)/3

Voila.

Inegalite 3

Soient a,b,c des reels strictement positifs tels que a+b+c = 1. Montrer que:

(a+1/a)^2+(b+1/b)^2+(c+1/c)^2>=100/3

Jolie. A toi de poster L inegalite 4

ok
inegalite 4 : (tres facile)
a,b,c>0 a,b,c # 1 et abc=1 M.Q : a^2\(a-1)^2 +b^2\(b-1)^2 +c^2\(c-1)^2>=3

prends a=b=c=1, ca donne: 3/4 > 1 ....

abdelkrim-amine a écrit:

ok
inegalite 4 : (tres facile)
a,b,c>0 et abc=1 M.Q : a^2\(a+1)^2 +b^2\(b+1)^2 +c^2\(c+1)^2>=1

fausse inegalité Mr "abdelkrim-amine" (prend a=b=c=1)
donner donc une autre vraie inegalité !!!

Syba a écrit:

prends a=b=c=1, ca donne: 3/4 > 1 ....

editer

younesmath2012 a écrit:

abdelkrim-amine a écrit:

ok
inegalite 4 : (tres facile)
a,b,c>0 et abc=1 M.Q : a^2\(a+1)^2 +b^2\(b+1)^2 +c^2\(c+1)^2>=1

fausse inegalité Mr "abdelkrim-amine" (prend a=b=c=1)
donner donc une autre vraie inegalité !!!

editer

abdelkrim-amine a écrit:

ok
inegalite 4 : (tres facile)
a,b,c>0 a,b,c # 1 et abc=1 M.Q : a^2\(a-1)^2 +b^2\(b-1)^2 +c^2\(c-1)^2>=1

Le début de la solution a l'air d'être ainsi:
On considère la fonction f définie par: sur .
On a donc et .
La dérivée seconde est strictement positive, f est donc convexe.
L'inégalité de la convexité nous donne alors: .
Ce qui se traduit par: .

Spoiler:

Je propose alors:
L'inégalité 5:
Soient des réels de l'intervalle [0,1[.
Démontrez que: .
Bonne chance.

nmo a écrit:

abdelkrim-amine a écrit:

ok
inegalite 4 : (tres facile)
a,b,c>0 a,b,c # 1 et abc=1 M.Q : a^2\(a-1)^2 +b^2\(b-1)^2 +c^2\(c-1)^2>=1

Le début de la solution a l'air d'être ainsi:
On considère la fonction f définie par: sur .
On a donc et .
La dérivée seconde est strictement positive, f est donc convexe.
L'inégalité de la convexité nous donne alors: .
Ce qui se traduit par: .

Spoiler:

c'est ma faute j'ai edite l'exo
en tous cas votre solution est vrai, a toi de poster une autre inego.

nmo a écrit:

Je propose alors:
L'inégalité 5:
Soient des réels de l'intervalle [0,1[.
Démontrez que: .
Bonne chance.

on peut mettre les deux cotes aux carre

J aimerais preiciser quelques points:

1) ca serait bien de poser de "belles inegalites". Il y en a beaucoup, il suffit de chercher un peu sur internet.
2) verifier d abord que l exercice est juste, et que la solution est interessante.
3) verifier aussi la solution que vous proposez. Par exemple: x*racine(1-x) n est pas la bonne fonction.
3) ecrire la derivee et de bien verifier qu elle convexe/concave.

Je me permets alors de proposer inegalite 6:

Inegalite 6: IMO 2001
Soient a, b, c des reels strictement positifs, montrer que:
a/racine(a^2+8bc)+b/racine(b^2+8ac)+c/racine(c^2+8ab)>=1

donc l'inegalite a demontrer est :

On considère la fonction f définie par:
donc

selon Jensen

donc il suffit de démontrer que : c'est faut
j'ai débloqué ici

P.S : je ne pense pas que cette inégo doit résoudre avec Jensen

la fonction est bonne mais les poids ne sont pas bons! essayes d abord de rendre a+b+c = 1 et utilises les comme poids...

C est un IMO, il doit pas etre trivail mais tu es sur la bonne voie