| | Applications de Inégalité arithmético-géométrique AM-GM |  |
|
+6Ahmed Taha (bis) galois einstein sadaso Oty younesmath2012 bel_jad5 10 participants |
|
| Auteur | Message |
|---|
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Applications de Inégalité arithmético-géométrique AM-GM  Ven 02 Nov 2012, 23:10 Ven 02 Nov 2012, 23:10 | |
| Ce lien est réservé à l'inégalité de la moyenne AM-GM. Celui qui résout l'exercice devra proposer un nouveau dans cette page et ainsi de suite.
http://fr.wikipedia.org/wiki/In%C3%A9galit%C3%A9_arithm%C3%A9tico-g%C3%A9om%C3%A9trique
Je commence: soient a,b,c des réels strictement positifs tels que abc = 1 . montrer que:
(ab+1)/(a+a²)+(bc+1)/(b+b²)+(ca+1)/(c+c²)>=3
à vous de jouer | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Ven 02 Nov 2012, 23:47 Ven 02 Nov 2012, 23:47 | |
| [img]http://latex.codecogs.com/gif.latex?on~~a~~:\frac{ab+1}{a+a^2}=\frac{ab(1+c)}{a(1+a)}~,~\frac{bc+1}{b+b^2}=\frac{bc(1+a)}{b(1+b)}~,~\frac{ca+1}{c+c^2}=\frac{ca(1+b)}{c(1+c)}\\\\donc~~\frac{ab+1}{a+a^2}+\frac{bc+1}{b+b^2}+\frac{ca+1}{c+c^2}\geq%203%20\sqrt[3]{\frac{ab+1}{a+a^2}\times\frac{bc+1}{b+b^2}\times\frac{ca+1}{c+c^2}}=3%20\sqrt[3]{\frac{ab(1+c)}{a(1+a)}\times\frac{bc(1+a)}{b(1+b)}\times\frac{ca(1+b)}{c(1+c)}%20}=3~~~~\blacksquare[/img] | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Ven 02 Nov 2012, 23:57 Ven 02 Nov 2012, 23:57 | |
| je propose l'exercice suivant : Inégalité2: }+\frac{1}{b(1+c)}+\frac{1}{c(1+a)}\geq%20\frac{3}{1+abc}) | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Dim 04 Nov 2012, 01:02 Dim 04 Nov 2012, 01:02 | |
| Allez les gars!!! quelqu un nous débarasse de celle là!!!  | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Dim 04 Nov 2012, 01:44 Dim 04 Nov 2012, 01:44 | |
| - younesmath2012 a écrit:
- je propose l'exercice suivant :
Inégalité2:
}+\frac{1}{b(1+c)}+\frac{1}{c(1+a)}\geq%20\frac{3}{1+abc}) on a deja résolue cette inégalité sur ce forum avec AM-GM , mais j'arrive pas a retrouver le lien , bon voici une autre solution différente que celle que j'avais proposé : on pose : abc=t^3 d'ou il existe x,y,z tel que : a=tx\y b=ty\z , c=tz\x. l'inégalité est equivalente a :  maintenant avec C-S : ^2}{(t+t^2)xyz(x+y+z)}\geq&space;\frac{3}{t+t^2}) car par AM-GM : (xy+yz+zx)² >= 3xyz(x+y+z) . ainsi il suffit de prouver : ^2(t+1)\geq&space;0) d'ou le resultat  . | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Dim 04 Nov 2012, 11:32 Dim 04 Nov 2012, 11:32 | |
| la9ta 3ajiba min la9atate Mr ''oty'' Bravo jolie reponse !!!
la balle a vous de choisir l'inegalité 3. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Dim 04 Nov 2012, 15:54 Dim 04 Nov 2012, 15:54 | |
| Merci Mr Younes , je propose celle si : (simple et faisable ) soit a,b,c ,d,e >= 0 , tel que : a+b+c+d+e=5 Montrer que : | |
|
  | |
sadaso
Maître
 Nombre de messages : 92 Nombre de messages : 92
Age : 29
Date d'inscription : 23/06/2011
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Dim 04 Nov 2012, 18:55 Dim 04 Nov 2012, 18:55 | |
| Un lien pour les inégalités utilisées ? | |
|
  | |
bel_jad5
Modérateur
 Nombre de messages : 529 Nombre de messages : 529
Age : 39
Date d'inscription : 07/12/2005
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Dim 04 Nov 2012, 19:34 Dim 04 Nov 2012, 19:34 | |
| Il y a une rubrique "théorèmes et formules" sur le site...le premier lien est bien pour commencer! | |
|
  | |
galois einstein
Maître

 Nombre de messages : 77 Nombre de messages : 77
Age : 29
Date d'inscription : 08/05/2012
 |  Sujet: solution Sujet: solution  Mer 21 Nov 2012, 02:40 Mer 21 Nov 2012, 02:40 | |
| - Oty a écrit:
- Merci Mr Younes , je propose celle si : (simple et faisable )
soit a,b,c ,d,e >= 0 , tel que : a+b+c+d+e=5
Montrer que :
Salut, je me tiens à proposer une solution pour l'exo de Oty: D'après AM-GM on a: (a+b+c)/3 >= 3v(abc) , et (b+c+d)/3 >= 3v(bcd) , et c'est la meme chose pour les autres. en sommant , on va obtenir: a+b+c+d+e=5 >= 3v(abc) +3v(bcd) +3v(cde) +3v(dea) +3v(eab) >= abc+bcd+cde+dea+eab (parce que a,b,c,d,e =< 1) je désigne par 3v(X), la racine cubique de X | |
|
  | |
galois einstein
Maître

 Nombre de messages : 77 Nombre de messages : 77
Age : 29
Date d'inscription : 08/05/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Mer 21 Nov 2012, 02:46 Mer 21 Nov 2012, 02:46 | |
| je propose l'exercice suivant:
soient a_2 , a_3 ,..., a_n des réels strictement positifs, tels que:
a_2 *a_3* ...* a_n =1 . montrer que:
(a_2 +1)^2 (a_3 +1)^3 ... (a_n +1)^n > n^n ;
avec n >= 3 un entier naturel | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Mer 21 Nov 2012, 09:22 Mer 21 Nov 2012, 09:22 | |
| - galois einstein a écrit:
- je propose l'exercice suivant:
soient a_2 , a_3 ,..., a_n des réels strictement positifs, tels que:
a_2 *a_3* ...* a_n =1 . montrer que:
(a_2 +1)^2 (a_3 +1)^3 ... (a_n +1)^n > n^n ;
avec n >= 3 un entier naturel prob de l'IMO 2012 ^i=\left&space;(&space;a_i+\frac{1}{i-1}+\frac{1}{i-1}+...+\frac{1}{i-1}&space;\right&space;)^i&space;%3E&space;\frac{i^{i}}{(i-1)^{i-1}}a_i) n'a pas d'égalité car 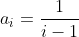 donc !}\neq&space;1) finalement ^{n-1}}\times&space;a_2a_3...a_n=n^n) | |
|
  | |
galois einstein
Maître

 Nombre de messages : 77 Nombre de messages : 77
Age : 29
Date d'inscription : 08/05/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Mer 21 Nov 2012, 13:24 Mer 21 Nov 2012, 13:24 | |
| | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Mer 21 Nov 2012, 14:11 Mer 21 Nov 2012, 14:11 | |
| - galois einstein a écrit:
- Oty a écrit:
- Merci Mr Younes , je propose celle si : (simple et faisable )
soit a,b,c ,d,e >= 0 , tel que : a+b+c+d+e=5
Montrer que :
Salut, je me tiens à proposer une solution pour l'exo de Oty:
D'après AM-GM on a:
(a+b+c)/3 >= 3v(abc) , et (b+c+d)/3 >= 3v(bcd) , et c'est la meme chose pour les autres.
en sommant , on va obtenir:
a+b+c+d+e=5 >= 3v(abc) +3v(bcd) +3v(cde) +3v(dea) +3v(eab) >= abc+bcd+cde+dea+eab
(parce que a,b,c,d,e =< 1)
je désigne par 3v(X), la racine cubique de X votre solution est fausse... parce que si a,b,c,d,e =< 1 et a+b+c+d+e=5 donc a=b=c=d=e=1 contre exemple a=3/2 , b=1/2 ,c=1 ,d=2/3 , e=4/3 | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Mer 21 Nov 2012, 14:26 Mer 21 Nov 2012, 14:26 | |
| exercice .. Soit a , b , Et c nombres réels positifs. Montrer que (b^5-b^2+3)(c^5-c^2+3)\ge (a+b+c)^3) bonne chance  | |
|
  | |
galois einstein
Maître

 Nombre de messages : 77 Nombre de messages : 77
Age : 29
Date d'inscription : 08/05/2012
 |  Sujet: re Sujet: re  Ven 23 Nov 2012, 00:27 Ven 23 Nov 2012, 00:27 | |
| - abdelkrim-amine a écrit:
- galois einstein a écrit:
- Oty a écrit:
- Merci Mr Younes , je propose celle si : (simple et faisable )
soit a,b,c ,d,e >= 0 , tel que : a+b+c+d+e=5
Montrer que :
Salut, je me tiens à proposer une solution pour l'exo de Oty:
D'après AM-GM on a:
(a+b+c)/3 >= 3v(abc) , et (b+c+d)/3 >= 3v(bcd) , et c'est la meme chose pour les autres.
en sommant , on va obtenir:
a+b+c+d+e=5 >= 3v(abc) +3v(bcd) +3v(cde) +3v(dea) +3v(eab) >= abc+bcd+cde+dea+eab
(parce que a,b,c,d,e =< 1)
je désigne par 3v(X), la racine cubique de X
votre solution est fausse...
parce que si a,b,c,d,e =< 1 et a+b+c+d+e=5 donc a=b=c=d=e=1
contre exemple a=3/2 , b=1/2 ,c=1 ,d=2/3 , e=4/3 Merci, j'ai pas fait attention :p | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Mer 16 Jan 2013, 19:14 Mer 16 Jan 2013, 19:14 | |
| http://www.codecogs.com/components/eqneditor/editor.php
pour retourner a la ligne \\ et espace \ | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Ven 25 Jan 2013, 00:38 Ven 25 Jan 2013, 00:38 | |
| - Oty a écrit:
- Merci Mr Younes , je propose celle si : (simple et faisable )
soit a,b,c ,d,e >= 0 , tel que : a+b+c+d+e=5
Montrer que :
Elle n'est plus facile mon cher; voyons ici: http://en.wikipedia.org/wiki/Maclaurin%27s_inequality. Je crois qu'elle se résout par cette dernière inégalité et non plus par l'inégalité arithmético-géométrique. | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Ven 25 Jan 2013, 11:58 Ven 25 Jan 2013, 11:58 | |
| sans perte de generalité on peut supposer par exemple e= min(a;b;c;d;e) donc 0<=e<=1 +e(a+c)(b+d)\leq%20(\frac{b+c+a+d-e}{3})^3+e(\frac{a+c+b+d}{2})^2\\=(\frac{5-2e}{3})^3+e(\frac{5-e}{2})^2%20=h(e)\\or%20h~~est~~croissante~(a~verifier)~donc~T\leq%20~h(1)=5) | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Ven 25 Jan 2013, 12:14 Ven 25 Jan 2013, 12:14 | |
| - younesmath2012 a écrit:
- sans perte de generalité on peut supposer par exemple e= min(a;b;c;d;e) donc 0<=e<=1
+e(a+c)(b+d)\leq%20(\frac{b+c+a+d-e}{3})^3+e(\frac{a+c+b+d}{2})^2\\=(\frac{5-2e}{3})^3+e(\frac{5-e}{2})^2%20=h(e)\\or%20h~~est~~croissante~(a~verifier)~donc~T\leq%20~h(1)=5) Joliie  Pourrais-tu poster une nouvelle inégo ? | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Ven 25 Jan 2013, 18:23 Ven 25 Jan 2013, 18:23 | |
| oui avec plaisir MR ''Humber'' (b-ca)(c-ab)\leq%208(abc)^{2}) | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Ven 25 Jan 2013, 19:30 Ven 25 Jan 2013, 19:30 | |
| (b-ca)(c-ab)\leq%208(abc)^{2}%20&\Longleftrightarrow%20a^2b^2+b^2c^2+c^2a^2+9a^2b^2c^2%20\geq%20abc(a^2+b^2+c^2+1)=2abc(1-\sum%20ab)\\%20%20&\Longleftrightarrow%20(ab+bc+ac)^2+9a^2b^2c^2%20\geq%202abc(2-\sum%20ab)%20%20\\%20&\Longleftrightarrow%20x^2+2xy+9y^2%20\ge%204y%20~~\text{Ou%20}%20x=\sum%20ab%20~~\text{Et%20}%20y=abc%20\\&\Delta_y=-16(2x-1)(x+1)%20\ge%200%20\\%20&\text{Donc%20:%20}%20x^2+2xy+9y^2%20\ge%204y%20\implies%20y%20\le%20\frac{1}{9}%20\left%20(-2\sqrt{-2x^2-x+1}-x+2%20\right%20)%20\end{aligned}%20\\%20\%20\begin{aligned}%20%20\end{aligned}) C'est vrai car : -la fonction f(x)= -2sqrt(-2x^2-x+1)-x+2 est strictement croissante sur [0,1/2] et donc f(x) <= f(1/2)=3/2 -D'après AM-GM y <= 1/27 <= (3/2)/9 = 1/6 Notons aussi que (a+b+c)²=a²+b²+c²+2(ab+bc+ac) ==> ab+bc+ac=x <= 1/2
Dernière édition par Humber le Sam 26 Jan 2013, 00:05, édité 6 fois | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Ven 25 Jan 2013, 21:10 Ven 25 Jan 2013, 21:10 | |
| | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Sam 26 Jan 2013, 00:06 Sam 26 Jan 2013, 00:06 | |
| - younesmath2012 a écrit:
(b-ca)(c-ab)\leq%208(abc)^{2}\Leftrightarrow%209a^2b^2c^2+a^2b^2+b^2c^2+c^2a^2\geq%20{\color{Blue}%20abc}+abc(a^2+b^2+c^2)) Merci pour votre vigilance  , J'ai modifié la solution | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  Sam 26 Jan 2013, 09:25 Sam 26 Jan 2013, 09:25 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM Sujet: Re: Applications de Inégalité arithmético-géométrique AM-GM  | |
| |
|
  | |
| | Applications de Inégalité arithmético-géométrique AM-GM |  |
|
