Applications de Inégalité arithmético-géométrique AM-GM

nmo a écrit:

Oty a écrit:

Merci Mr Younes , je propose celle si : (simple et faisable )
soit a,b,c ,d,e >= 0 , tel que : a+b+c+d+e=5
Montrer que :

Elle n'est plus facile mon cher; voyons ici: http://en.wikipedia.org/wiki/Maclaurin%27s_inequality.
Je crois qu'elle se résout par cette dernière inégalité et non plus par l'inégalité arithmético-géométrique.

Avec L'inégalité de Maclaurin cher ami nmo on trouve les permutations des élements (sygma sym) et non sygma
cyc , ici on a 5 èlèment (abc,bcd,cde,dea,eab) mais en faite pour appliquer maclaurin il faut encore 5 èlements
de Plus car :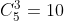
Amicalement .