*youness*
Maître
 Nombre de messages : 132
Date d'inscription : 16/08/2011
 | | Sujet: Inégalité Trés Compliquée Ven 30 Nov 2012, 23:51 | |
|
Dernière édition par *youness* le Sam 01 Déc 2012, 15:39, édité 1 fois | |
|
*youness*
Maître
Nombre de messages : 132
Date d'inscription : 16/08/2011
| | Sujet: Re: Inégalité Trés Compliquée Sam 01 Déc 2012, 13:22 | |
| | |
|
Oty
Expert sup
Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
| | Sujet: Re: Inégalité Trés Compliquée Sam 01 Déc 2012, 13:34 | |
| c pas compliqué du tout , mais c l'exo 3 de l'olympiade qu'on a passé hier , il faut attendre confirmation pour pouvoir posté nos solution , car a ce qui parait une region n a po encore pasé | |
|
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Inégalité Trés Compliquée Sam 22 Déc 2012, 00:12 | |
| Le problème est de démontrer que 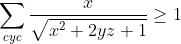 sachant que les réels x, y et z vérifient 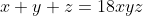 . On a 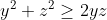 , donc 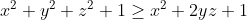 , donc 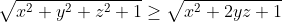 soit 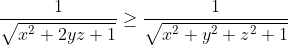 . De même, on démontre que 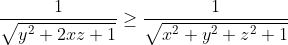 et 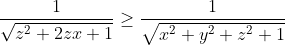 . Donc 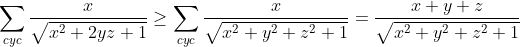 . Il suffit donc de prouver que 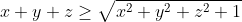 ou encore ^2\ge x^2+y^2+z^2+1) . Cela revient à démontrer que 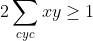 . Or, on a selon l'inégalité arithmético-géométrique: (\sum_{cyc}xy)\ge9xyz) . Donc \ge9xyz) soit finalement 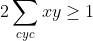. CQFD. Sauf erreurs! | |
|
Contenu sponsorisé
| | Sujet: Re: Inégalité Trés Compliquée | |
| |
|
