aissa
Modérateur
 Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
 | | Sujet: sous espace stable Mar 14 Mai 2013, 22:13 | |
| salut tout le monde
Soit f un endomorphisme de IR^3 nilpotent d'indice 2 et F un plan de IR^3 stable par f
montrer que Im(f) C F
bon courage | |
|
galillee56
Expert grade2
Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
| | Sujet: Re: sous espace stable Mer 15 Mai 2013, 17:03 | |
| soit a un element n'appartenant pas a ker f et c un element appartenant a ker f n'appartenant pas a vect(f(a)) (a,f(a),c) forme une base dans cette base la matrice de f est 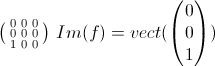 soit X=(x,y,z) dans F en multpliant par la par la matrice de f on trouve que la droite porter par (0,0,1) appartient a F soit encore Im(f) appartient F | |
|
galillee56
Expert grade2
Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
| | Sujet: Re: sous espace stable Mer 15 Mai 2013, 17:08 | |
| ma matrice est dans la base (a,c,f(a)) | |
|
aissa
Modérateur
Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
| | Sujet: Re: sous espace stable Mer 15 Mai 2013, 21:48 | |
| Bonsoir galille56
oui c"est bien ça
on peux voir aussi que f² =o => Im(f) C Ker(f)
d'aprés le théorème du rang on a rg(f)=1 (dim(Ker(f) +rg(f) =3)
F plan stable par f alors
i) F = ker(f) C Im(f)
ii) ou bien F différent de Ker(f) alors il existe u dans F ; f(u) non nul
alors Im(f) = vect(f(u)) C F
Donc gans tout les cas Im(f) C F
Amicalement | |
|
galillee56
Expert grade2
Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
| | Sujet: Re: sous espace stable Dim 19 Mai 2013, 23:30 | |
| merci beaucoup pour votre methode Mr aissa et je m'excuse d'avoir tarder a repondre | |
|
aissa
Modérateur
Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
| | Sujet: Re: sous espace stable Lun 20 Mai 2013, 19:25 | |
| Bonsoir galillee56 y a pas de quoi je m excuse moi aussi pour le retard | |
|
Contenu sponsorisé
| | Sujet: Re: sous espace stable | |
| |
|
