|
| | marathon de préapration à l'entrée sup 2013/2014. |  |
|
+5boubou math Oty solixos Mohammed_Lahlou Syba 9 participants | |
| Auteur | Message |
|---|
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: marathon de préapration à l'entrée sup 2013/2014. Sujet: marathon de préapration à l'entrée sup 2013/2014.  Jeu 29 Aoû 2013, 23:33 Jeu 29 Aoû 2013, 23:33 | |
| Bonsoir,
Je me permets de créer ce sujet en guise de marathon, qui vise notre préparation et notre mise en route pour intégrer les classes préapratoires. Les exercices proposés ici, seront le plus souvent des exercices de niveau sup mais de n'importe quelle difficulté. Il serait quand meme préférable que seuls les étudiants sup y participent, et que les exercices soient de difficulté moyenne à difficile pour bien nous entrainer.
Sinon, les règles sont très simples:
*Celui qui résout un problème, en pose un autre, et ainsi de suite.
*Chaque solution doit etre claire et lisible, chaque problème numéroté.
Bon jeu !
Dernière édition par Syba le Ven 30 Aoû 2013, 00:03, édité 1 fois | |
|   | | Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Jeu 29 Aoû 2013, 23:47 Jeu 29 Aoû 2013, 23:47 | |
| Problème 1:Soit a un réel de l'intervalle 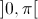 , calculer:  Bonne chance ! | |
|   | | Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 30 Aoû 2013, 02:23 Ven 30 Aoû 2013, 02:23 | |
| - Syba a écrit:
- Problème 1:
Soit a un réel de l'intervalle 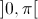 , calculer: , calculer:

Bonne chance ! Solution 1: je note : TT : produit allant k=1 jusqu'à n Soit a le réel qu'on à, on s'interesse à calculer la somme des ln(cos(a/2^k)) soit ln(TTcos(a/2^k)). On sait bien que pour tout x £ R, sin(2x)=2sin(x)cos(x), et puisque sin(a/2^k) diffère zéro ( a £ ]0,TT[ ) alors cos(a/2^k)=1/2*sin(a/2^(k-1))/sin(a/2^k). En posant pour tout 1=<k=<n, a_k = sin(a/2^(k) cos(a/2^k) = 1/2* a_(k-1) / a_(k), donc TTcos(a/2^k)=(1/2^n)TT(a_(k-1)/a_(k)). Par un telescopage TTcos(a/2^k) = (1/2^n)*sin(a)/sin(a/2^n). Il s'ensuit que, la somme des ln(cos(a/2^k)) = ln(1/2^n*sin(a))/(sin(a/2^n)) = ln(sin(a))-ln(2^n*sin(a/2^n)) On considère la fonction f définie sur R par, ~f(x) = sin(ax)/x si x £ R*, ~f(0)=a, On a f(1/2^n)= 2^n*sin(a/2^n), puis lim (1/2^n) = 0 au passage à la limite, lim 2^n*sin(a/2^n) = f(lim(1/2^n))=f(0)= a (f est bien continue au point 0 ) et ln est continue au point a puisque a £ ]0,TT[ donc lim ln(2^n*(sin(a/2^n)) = ln(a). Conclusion la limite proposée est égale a ln(sin(a)/a). Sauf erreurs.
Dernière édition par Mohammed_Lahlou le Ven 30 Aoû 2013, 11:45, édité 3 fois | |
|   | | solixos
Débutant
 Nombre de messages : 7 Nombre de messages : 7
Age : 29
Date d'inscription : 06/12/2011
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 30 Aoû 2013, 02:27 Ven 30 Aoû 2013, 02:27 | |
| | |
|   | | Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 30 Aoû 2013, 02:28 Ven 30 Aoû 2013, 02:28 | |
| Exercice2:
Soit {1,...,p} et {1,...,n} deux ensembles avec (n,p)£ lN*
1) Trouvez le nombre d'applications croissantes de {1,...,p} vers {1,...,n}
2) Trouvez le nombre d'applications strictement croissantes de {1,...,p} vers {1,...,n} | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 30 Aoû 2013, 05:13 Ven 30 Aoû 2013, 05:13 | |
| jolie question proposé a l'exercice 2) voici une tentative : 1) on suppose que n >= p , sinon pour p> n c'est impossible parce qu'une application strictement croissante et forcement injective . Pour construire de telles applications ,l'ensemble H={f(1),f(2),...,f(p)} est tel que1=< f(1) < f(2) < ... < f(p)=< n et inclus dans [[1,n]] donc H est une partie de {1,...,n} a p éléments totalement ordonné , il s'en suit que le nombre d'application strictement croissante est egal au nombre de partis de {1,...,n} a p élément qui n'est autre que 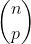 2) soit f une application croissante de {1,...,p} vers {1,...,n} l'ensemble H={f(1),f(2),..,f(p)} est tel que 1=<f(1)=< f(2)=< ..=<f(p)=< n , on définie une suite x_{k}=f(k) pour tout k de {1,....,p} on a bien 1=<x_{1}=<x_{2}=<...=< x_{p}=< n ou il s'ensuite que 1=<x_{1}< x_{2}+1 < x_{3}+2 < ... < x_{p}+p-1 =< n+p-1 on pose y_{k}=x{k}+k-1 , pour tout k entre {1,....,p} on : 1=< y_{1} < y_{2} < .... < y_{p}=<n+p-1 on vérifie facilement que y_{k} est une suite strictement croissante a valeurs dans {1 , ..., n+p-1} et que pour chaque y_{k} qu'on définie dans {1,....,n+p-1} x_{m} est bien définie dans {1,...,n} (m fixé)(*) et puis que l'ensemble {y_{1} , .... , y_{p}} définie une application strictement croissante de {1 ,....,p} vers {1,....,n+p-1} , il s'ensuit que le nombre d'applications croissantes est  | |
|   | | Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 30 Aoû 2013, 11:53 Ven 30 Aoû 2013, 11:53 | |
| Rien à dire Oty  , à toi. | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 30 Aoû 2013, 14:48 Ven 30 Aoû 2013, 14:48 | |
| Probleme 3 :
Soit f une fonction continue sur un segment I=[a,b] . On suppose que f vérifie la propriété suivante :
pour tous les points c < d de l'intervalle I , il existe e compris entre c et d tel que
f(e)=f(a) ou f(e)=f(b) . Montrer que f est constante . | |
|   | | Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 30 Aoû 2013, 15:29 Ven 30 Aoû 2013, 15:29 | |
| - Oty a écrit:
- Probleme 3 :
Soit f une fonction continue sur un segment I=[a,b] . On suppose que f vérifie la propriété suivante :
pour tous les points c < d de l'intervalle I , il existe e compris entre c et d tel que
f(e)=f(a) ou f(e)=f(b) . Montrer que f est constante . Solution 3:si a=b, on vérifie que la fonction est à valeure dans {a} si a<b. On suppose que f soit non constante alors il existe un x dans [a,b] tq : f(x) =/= f(b) (sans noter respectivement f(a)) x<b, donc il existe un a_n, tq x<a_n<b, vérifiant f(a_n)=f(b) (ou f(a)), ainsi il existerait un a_(n-1) vérifiant a_n<a_(n-1)<b, et avec cela on creé une suite réel (a_n)n>=1 tq x<a_n<...<a_1<b avec f(b)=f(a_n) la suite (a_n) est décroissante et minorée par x, donc converge vers x, au passage à la limite et puisque f est continue en tout point de [a,b] f(b)=limf(a_n)=f(lim(a_n))=f(x) ce qui est contradictoire à la supposition. Sauf erreurs.
Dernière édition par Mohammed_Lahlou le Sam 31 Aoû 2013, 16:05, édité 3 fois | |
|   | | Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 30 Aoû 2013, 16:15 Ven 30 Aoû 2013, 16:15 | |
| - Mohammed_Lahlou a écrit:
la suite (a_n) est décroissante et minorée par x, donc converge vers x
c'est à prouver je pense ! | |
|   | | Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 30 Aoû 2013, 17:18 Ven 30 Aoû 2013, 17:18 | |
| - Syba a écrit:
- Mohammed_Lahlou a écrit:
la suite (a_n) est décroissante et minorée par x, donc converge vers x
c'est à prouver je pense ! EDIT : Merci pour la rectification de ma faute concernant la monotonie de la suite déjà *Toute suite croissante et majorée converge vers sa borne supérieur.
Dernière édition par Mohammed_Lahlou le Ven 30 Aoû 2013, 21:15, édité 1 fois | |
|   | | Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 30 Aoû 2013, 17:30 Ven 30 Aoû 2013, 17:30 | |
| Problème 4:
~On note int(0,1)f : l'intégrale de 0 à 1 de f(x)dx
~V : la racine carée
1) Soient f,g : [0,1] --> lR deux fonctions continues, monotones et de même monotonie. Démontrez que (int(0,1)f)(int(0,1)g) =< int(0,1)f*g
2) Soit f : [0,1] -> R+ une fonction continue, on note I = int(0,1) f,
Démontrez que : V(1+I²) =< int(0,1) V(1+f²) =< 1+I
| |
|   | | Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 30 Aoû 2013, 23:58 Ven 30 Aoû 2013, 23:58 | |
| Bonsoir, C'est un très bon exrcice, j'ai essayé la première question d'abord. Pour la deuxième, il me reste à prouver la partie gauche. Au début, j'ai essayé d'utiliser CS, mais en vain. Puis, j'y suis allé bourrin en utilisant la différence de deux fonctions, et son étude. La encore, j'avais un problème. Je ne trouvais rien d'intéressant pour pouvoir exploiter les conditions que vérifient les deux fonctions. Finalement, j'ai essayé d'ajouter un x, comme ca je me suis trouvé avec 4 produits, et donc j'ai factorisé et fait appel aux données pour la suite. Voila un peu mon histoire avec ce problème qui m'a pris plus de 5 heures de réflexion hhh. On considère la fonction Phi, définie par: 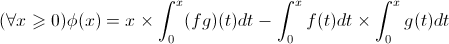 On vérifie facilement que la fonction Phi est dérivable, et qu'on a:  Ou encore, en factorisant:  La, on fait une disjonction de cas, (f et g croissantes) ou (f et g décroissantes). Il s'ensuit que le produit est positif, et qu'alors l'intégrale est positive, et donc l'expression Phi'(x) est positive sur [0,1]. Alors, la fonction Phi est croissante sur [0,1]. Donc: x > 0 ==> Phi(x) > Phi(0) ==> Phi(x) > 0 x = 0 ==> Phi(x) = 0 Particulièrement, pour x = 1, on trouve finalement le résultat souhaité:  Sauf erreurs ! | |
|   | | Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 00:42 Sam 31 Aoû 2013, 00:42 | |
| Rebonsoir, Pour la deuxième question: Le coté gauche, je crois(j'attends votre confirmation) qu'on applique directement l'inégalité de Jensen: On considère la fonction convexe h, définie sur R par:  On a alors, d'après Jensen:  (*) D'autre part, pour tous x de [0,1]:  Ou encore, pour tous x de [0,1]:  (**) De (*) et (**), on déduit le résultat voulu. Sauf erreurs ! | |
|   | | Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 01:11 Sam 31 Aoû 2013, 01:11 | |
| Bravo Syba  ! à ton tour. | |
|   | | Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 10:25 Sam 31 Aoû 2013, 10:25 | |
| Problème 5:1) Soient a,b ∈ Q+, tels que √(a) et √(b) soient irrationnels. Montrer que √(a) + √(b) est irrationnel. 2)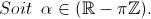 Montrer que l'existence d'une des deux limites  , entraine celle de l'autre et que l'existence des deux entraine une contradiction. Bonne chance ! | |
|   | | Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 17:02 Sam 31 Aoû 2013, 17:02 | |
| Solution 5:
1) Soient a,b ∈ Q+, tels que √(a) et √(b) soient irrationnels.
si a=b on suppose que 2√a soit rationnel alors √a est rationnel d'où la contradiction.
si a est différente de b.
On suppose que √(a)+√(b) soit rationnel (*). on sait que (√(a)+√(b))(√(a)-√(b))=a-b
donc √(a)-√(b) = (a-b)/(√(a)+√(b)) puisque (a-b) est rationnel alors √(a)-√(b) (**) est également rationnel en sommant (*) et (**) 2√(a) est rationnel donc √(a) est rationnel ce qui contradit l'ennoncé.
(Tentation j'attends votre confirmation pour celle-ci, si je ne dis pas de bétises)
2) Soit a ∈ (lR - PiZ)
*Supposons que sin(na) admet une limite, puisque -1=<sin(na)=<1, donc la limite est finie posant lim sin(na)= l
on sait que sin(na)²+cos(na)²=1, donc cos(na)= (+-)√(1-sin(na)²) au passage à la limite la limite de cos(na) = √(1-l²), donc si l'une existe l'autre existe aussi
*Supposons l'existence des deux limites à la fois.
sin(na)cos(a)=1/2[sin(na+a)+sin(na-a)] => sin(na+a)+sin(na-a)=2sin(na)cos(a) en fesant tendre n vers l'inf, on obtient 2d=2dcos(a) (avec d la limite du sin), donc cos(a)=1, ou d = 0 puisque a est diff de PiZ donc d = 0, d'autre par sin(na+a) = sin(na)cos(a)+sin(a)cos(na) en fensant tendre n vers l'inf 2d=dc+sin(a)c donc c(sin(a))=0, sin est diff de 0 donc c=0, fait que les deux limites égales à 0, mais on a cos(na)²+sin(na)²=1, au voisinage de l'inf. contradiction.
Dernière édition par Mohammed_Lahlou le Sam 31 Aoû 2013, 18:21, édité 2 fois | |
|   | | boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 17:04 Sam 31 Aoû 2013, 17:04 | |
| je propose ma démarche pour l'exo proposé auparavant par mohammed Il suffit de se rappeler de l'identité des sommes de Riemann. l'inégalité alors est équivalente à montrer que : )(\lim_{n\rightarrow&space;+\propto&space;}(\frac{1}{n}\sum_{0}^{n-1}g(\frac{k}{n}))\leq&space;\lim_{n\rightarrow&space;+\propto&space;}(\frac{1}{n}\sum_{0}^{n-1}f(\frac{k}{n})g(\frac{k}{n}))) le reste n'est rien d'autre que l'inégalité de Tchebychev et un passage à la limite .
Dernière édition par boubou math le Sam 31 Aoû 2013, 22:24, édité 1 fois | |
|   | | Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 17:26 Sam 31 Aoû 2013, 17:26 | |
| - Mohammed_Lahlou a écrit:
- Solution 5:
on sait que sin(na)²+cos(na)²=1, donc cos(na)= √(1-sin(na)) au passage à la limite la limite de cos(na) = √(1-l), donc si l'une existe l'autre existe aussi. la fonction cos n'est pas toujours positive, de plus t'as oublié le signe carré pour sin(na) et pour l. sinon, je pense que c'est juste, meme si j'ai utilisé une autre methode. pour le reste, c'est bon, j'ai fait presque la meme chose. à toi de proposer un problème ! | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 17:33 Sam 31 Aoû 2013, 17:33 | |
| - Mohammed_Lahlou a écrit:
Solution 3:
si a=b, on vérifie que la fonction est à valeure dans {a}
si a<b.
On suppose que f soit non constante alors il existe un x dans [a,b] tq : f(x) =/= f(b) (sans noter respectivement f(a))
x<b, donc il existe un a_n, tq x<a_n<b, vérifiant f(a_n)=f(b) (ou f(a)), ainsi il existerait un a_(n-1) vérifiant a_n<a_(n-1)<b, et avec cela on creé une suite réel (a_n)n>=1 tq x<a_n<...<a_1<b avec f(b)=f(a_n) la suite (a_n) est décroissante et minorée par x, donc converge vers x, désolé mais ce qui est en rouge est faux ! ou sinon il faut le prouvé . d'ailleurs f(an)=f(b) c'est faux , l’énonce stipule qu"il exite f(e)=f(a) ou f(e)=f(b) , l'existance ne te permets de choisir $e$ entre x et b | |
|   | | Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 17:58 Sam 31 Aoû 2013, 17:58 | |
| Bon comme l'exercice (3) est dépassé je propose ma solution que j'espere valable : comme f est continue et d'apres l’hypothèse , on va essayé de montrer que [img]http://latex.codecogs.com/gif.latex?\forall&space;x\in&space;[a,b]&space;|&space;f(x)=f(a)&space;~~ou~~f(x)=f(b)[/img] ce qui permettra de conclure par continuité de f , on suppose par l'absurde qu'il [img]http://latex.codecogs.com/gif.latex?\exists&space;x_{o}&space;\in&space;[a,b]&space;:&space;f(x)\neq&space;f(a)~~et~~f(x)\neq&space;f(b)[/img] comme : =f(x_{0})) et d'apres notre supposition |f(xo)-f(a)| > 0 et |f(x_{o})-f(b)| > 0 , on pose : -f(x_{0})|,|f(b))-f(x_{0})|)}{2}) on prenant e=a , il exite un intrevalle [xo - r , xo+r] inclue dans [a,b] avec r > 0 tel que pour tout x dans cette intervalle |f(x)-f(xo)|< a or comme xo-r < xo+r il existe e1 dans cette intervalle tel que f(e1)=f(a) ou f(e1)=f(b) et |f(e)-f(xo)| < a , contraction ! et donc quelque soit x dans [a,b] ; f(x)=f(a) ou f(x)=f(b) ce qui permet de conclure par continuité de f . | |
|   | | Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 18:12 Sam 31 Aoû 2013, 18:12 | |
| @Oty : Au temps pour moi .., belle solution. @Syba : merci c'était des fautes d'inatention  , je rédiges direct sur le forum. (c'est édité) Problème 6:Soit B une partie bornée non vide de C On suppose que si z £ B alors 1-z+z² £ B et 1+z²+z £ B Déterminer B. | |
|   | | boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 21:50 Sam 31 Aoû 2013, 21:50 | |
| Comment peut-on définir une partie borné de C ? | |
|   | | Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 21:52 Sam 31 Aoû 2013, 21:52 | |
| lol je me suis posé la meme question, j'att toujours sa reponse .
Dernière édition par Syba le Sam 31 Aoû 2013, 23:02, édité 1 fois | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Sam 31 Aoû 2013, 22:03 Sam 31 Aoû 2013, 22:03 | |
| Une partie bornée de C, est un ensemble de points dont le module est majoré par une certaine constante, càd il existe un disque dans C qui contient cette partie. | |
|   | | Contenu sponsorisé
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  | |
| |
|   | | | | marathon de préapration à l'entrée sup 2013/2014. |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
