| | marathon de préapration à l'entrée sup 2013/2014. |  |
|
+5boubou math Oty solixos Mohammed_Lahlou Syba 9 participants |
|
| Auteur | Message |
|---|
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Dim 01 Sep 2013, 15:32 Dim 01 Sep 2013, 15:32 | |
| Solution 6:
On sait que l'ensemble B n'est pas vide.
Ainsi, on remarque que i et -i appartiennent à B (vérification directe).
Notons (z_n) la suite d'éléments de B, définie par z_0 = x, et:
z_(n+1) = f(z_n) = 1+(z_n)+(z_n)², si Re(z_n) < 0.
z_(n+1) = g(z_n) = 1+(z_n)+(z_n)², si Re(z_n) >= 0.
On considère la suite (U_n) définie par: |(z_n)²+1|.
Alors:
U_(n+1)
=|(z_(n+1))²+1|
=|(z_(n+1)-i|.|z_(n+1)+i|
=|1-i+(z_n)+(z_n)²|.|1+i+(z_n)+(z_n)²|
=|((z_n)-i)((z_n)+i+1)|.|((z_n)+i)((z_n)-i+1)|
=U_n.|(z_n)-(i+1)|.|(z_n)-(1-i)|
On pose (z_n)= a+bi, avec a et b des réels.
|(a-1)+(b-1)i|= √[(a-1)²+(b-1)²]
|(a-1)+(b+1)i|= √[(a-1)²+(b+1)²]
Dans tous les cas (sachant que a<0), le produit des 2 modules est supérieur à √(2) .
Ainsi, U_(n+1) >= √(2) U_(n) .
Alors, la suite (U_n) n'est pas bornée. Or B elle, est bornée.
D'ou: U_0 = 0. Donc: x=i ou x=-i.
De la meme facon, si z_(n+1) = g(z_n).
Résultat: B={-i,i}.
Sauf erreurs ! | |
|
  | |
Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Dim 01 Sep 2013, 15:45 Dim 01 Sep 2013, 15:45 | |
| C'est la bonne solution Syba  à ton tour. | |
|
  | |
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Dim 01 Sep 2013, 15:55 Dim 01 Sep 2013, 15:55 | |
| Problème 7:
Soit n un entier naturel, non premier, strictement supérieur à 5.
Montrer que: n / (n-2)!
Bonne chance ! | |
|
  | |
Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Dim 01 Sep 2013, 17:53 Dim 01 Sep 2013, 17:53 | |
| Solution 7:
Soit n un entier naturel, non premier, strictement supérieur à 5,
on démontre d'abord que n | (n-1)!
Pour cela on décompose n en facteurs premiers n = TT(pi^(ai)), tout les p_i sont premiers, et strictement inférieur à n puisque n n'est pas premier donc inférieur ou égal à (n-1) et donc sont tous parmis les facteurs de (n-1)! et donc divisent (n-1)! (à noter que pour tout i les pi^(ai) sont inférieur ou égal à (n-1))
Puisqu'il sont premiers entre eux on applique (a|c et b|c avec pgcd(a,b)=1 => ab|c) ( de plus on sait que pgcd(a,b)=1 => pgcd(a^q,b^k)=1) pour tout les nombres premiers et donc TT(pi^(ai))| (n-1)! => n | (n-1)!
On sait que n | (n-1)! donc n | (n-2)!(n-1), par bezout on vérifie immédiatement que pgcd(n,n-1)=1
Par gauss n | (n-2)!
Sauf erreurs. | |
|
  | |
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Dim 01 Sep 2013, 19:35 Dim 01 Sep 2013, 19:35 | |
| t'as traité seulement le cas des nombres: n, ou les p_i sont differents 2 a 2,
t'as pas traité le cas des nombres: n = p^k, ou p est un nombre premier, k un entier naturel strictement supérieur à 1.
| |
|
  | |
Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Dim 01 Sep 2013, 19:54 Dim 01 Sep 2013, 19:54 | |
| le cas de p^k | (p^k -1)!, pour 1=<i=<k-1 1=<p^i < p ^k et donc 1 =< p^i =< p^(k) -1 donc TT(p^i) =< (p^(k)-1)! et donc p^k(k-1)/2 | (p^(k)-1)! et puisque k(k-1)/2 => k donc p^k | p^k(k-1)/2 | (p^(k)-1)!. Conclure, désolé pour l'ambiguité.
Problème 8:
TT désignant le produit (de k=1 jusqu'à n), ∑ désignant la somme (de k=1 jusqu'à n)
Soit n £ lN* et D = {z £ C, |z|=<1 }, a_1, ...,a_n, b_1,...,b_n £ D
Montrer que :
|TT(a_k)-TT(b_k)| =< ∑|(a_k)-(b_k)| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Lun 14 Juil 2014, 09:59 Lun 14 Juil 2014, 09:59 | |
| - Mohammed_Lahlou a écrit:
- Problème 8:
TT désignant le produit (de k=1 jusqu'à n), ∑ désignant la somme (de k=1 jusqu'à n)
Soit n £ lN* et D = {z £ C, |z|=<1 }, a_1, ...,a_n, b_1,...,b_n £ D
Montrer que : |TT(a_k)-TT(b_k)| =< ∑|(a_k)-(b_k)| On procède par récurrence sur l'entier  . *Initialisation: L'inégalité est triviale pour 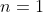 . Pour 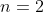 , on doit démontrer que : |ab-xy|\le |a-x|+|b-y|) . En effet, soient  ,  ,  et  des complexes appartenant au disque unité. On a 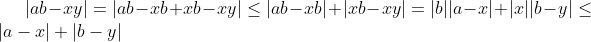 . On conclût que la propriété est vraie au rang 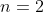 . *Hérédité: On suppose que la propriété est vraie au rang  , c'est à dire que : |\prod_{k=1}^{n}a_k-\prod_{k=1}^{n}b_k|\le\sum_{k=1}^{n}|a_k-b_k|) . Et on doit démontrer qu'elle est vraie au rang 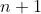 , c'est à dire que : |\prod_{k=1}^{n+1}a_k-\prod_{k=1}^{n+1}b_k|\le\sum_{k=1}^{n+1}|a_k-b_k|) . Soient 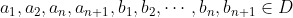 . On a 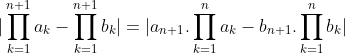 et 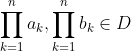 . L'hypothèse de récurrence pour 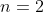 donne 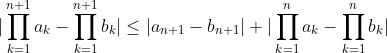 . Et l'hypothèse de récurrence à l'ordre  fournit que 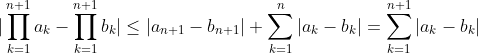 . *Conclusion de la récurrence: : (\forall a_1,\cdots,a_n,b_1,\cdots,b_n\in D): |\prod_{k=1}^{n}a_k-\prod_{k=1}^{n}b_k|\le\sum_{k=1}^{n}|a_k-b_k|) . Sauf erreurs. | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Mar 15 Juil 2014, 11:50 Mar 15 Juil 2014, 11:50 | |
| - Oty a écrit:
- Bon comme l'exercice (3) est dépassé je propose ma solution que j'espere valable :
comme f est continue et d'apres l’hypothèse , on va essayé de montrer que
[img]http://latex.codecogs.com/gif.latex?\forall&space;x\in&space;[a,b]&space;|&space;f(x)=f(a)&space;~~ou~~f(x)=f(b)[/img]
ce qui permettra de conclure par continuité de f ,
on suppose par l'absurde qu'il
[img]http://latex.codecogs.com/gif.latex?\exists&space;x_{o}&space;\in&space;[a,b]&space;:&space;f(x)\neq&space;f(a)~~et~~f(x)\neq&space;f(b)[/img]
comme : =f(x_{0}))
et d'apres notre supposition |f(xo)-f(a)| > 0 et |f(x_{o})-f(b)| > 0 ,
on pose : -f(x_{0})|,|f(b))-f(x_{0})|)}{2})
on prenant e=a , il exite un intrevalle [xo - r , xo+r] inclue dans [a,b] avec r > 0 tel que pour tout x dans cette intervalle
|f(x)-f(xo)|< a or comme xo-r < xo+r il existe e1 dans cette intervalle tel que f(e1)=f(a) ou f(e1)=f(b)
et |f(e)-f(xo)| < a , contraction !
et donc quelque soit x dans [a,b] ; f(x)=f(a) ou f(x)=f(b) ce qui permet de conclure par continuité de f . Une autre solution : Soit g(x)=(f(x)-f(a))(f(x)-f(b)) L'hypothèse ==> qqs a<x<b et qqs n entier assez grand il existe x-1/n<x_n<x+1/n : g(x_n)=0. or g est continue sur [a,b] et x_n-->x ==> g(x)=0. Donc g est nulle sur [a,b] ..... | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Lun 21 Juil 2014, 19:24 Lun 21 Juil 2014, 19:24 | |
| l'exercice 7 :
n est composé .
Alors on a l'existence de a et b tel que :
n=a*b avec a>=2 et b>=2
Si a=! b:
Alors a<=n/2 et b<=n/2 et n/2<n-2 pour n>4 implique (n-2)!=1*2*..*a*...*b*..(n-2)=k*n
Si a=b :
Alors n=a² et on a n>=9 or vu que 2rac(n)<n-2 pour n>=9 on deduit que :
(n-2)!=1*2*...*a*...*2a*...*(n-2)=k*n | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Mar 25 Aoû 2015, 11:16 Mar 25 Aoû 2015, 11:16 | |
| Je propose un nouvel exercice: Problème 9:Est ce que le nombre 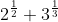 est rationnel? Bonne chance. | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  Ven 28 Aoû 2015, 17:20 Ven 28 Aoû 2015, 17:20 | |
| Pb 9
Soit x le réel en question
(x-V2)^3=3
x^3-3x^2V2+6x-2V2=3
Si x rationnel, alors 3x^2+2=0 impossible | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: marathon de préapration à l'entrée sup 2013/2014. Sujet: Re: marathon de préapration à l'entrée sup 2013/2014.  | |
| |
|
  | |
| | marathon de préapration à l'entrée sup 2013/2014. |  |
|
