| | Monde des équations fonctionnelles |  |
|
+10aymas nmo elidrissi aymanemaysae Amine Natik Humber charaf_X legend-crush Ahmed Taha L-W-P 14 participants |
|
| Auteur | Message |
|---|
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Monde des équations fonctionnelles Sujet: Monde des équations fonctionnelles  Jeu 16 Jan 2014, 17:41 Jeu 16 Jan 2014, 17:41 | |
| Exo 1
pour commencer
trouvez toutes fonctions de R-----R qui vérifient
f(x).f(y)=f(x-y).
celui qui répond qu'il poste et numérote | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Jeu 16 Jan 2014, 18:07 Jeu 16 Jan 2014, 18:07 | |
| - L-W-P a écrit:
- Exo 1
pour commencer
trouvez toutes fonctions de R-----R qui vérifient
f(x).f(y)=f(x-y).
celui qui répond qu'il poste et numérote - Solution Exo 1 ::
supposons P(x,y)=>f(x).f(y)=f(x-y)
P(0,0)=>f(0)=0 ou f(0)=1
-si f(0)=0
P(x,x)=>f²(x)=0 =>f(x)=0
-si f(0)=1
P(x,x)=>f²(x)=1 =>f(x)=1
Exo 2Trouver toutes les fonctions f:R--->R telles que : 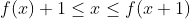 | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Jeu 16 Jan 2014, 18:10 Jeu 16 Jan 2014, 18:10 | |
| on note P(x;y): f(x)f(y)=f(x-y)
- P(0;0) , f²(0)=f(0) <--> f(0)=1 ou f(0)=0
- P(x;x) , f²(x)=f(0) , si f(0)=0 alors f(x)=0 et si f(0)=1 alors f(x)=1 ou f(x)=-1 (or ce dernier cas n'est pas solution.
Donc: f(x)=0 ou f(x)=1
sauf erreur .
P.S: je viens de voir qu'Ahmed Taha vient lui aussi de poster la réponse :p | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Jeu 16 Jan 2014, 18:20 Jeu 16 Jan 2014, 18:20 | |
| - legend-crush a écrit:
- on note P(x;y): f(x)f(y)=f(x-y)
- P(0;0) , f²(0)=f(0) <--> f(0)=1 ou f(0)=0
- P(x;x) , f²(x)=f(0) , si f(0)=0 alors f(x)=0 et si f(0)=1 alors f(x)=1 ou f(x)=-1 (or ce dernier cas n'est pas solution.
Donc: f(x)=0 ou f(x)=1
sauf erreur .
P.S: je viens de voir qu'Ahmed Taha vient lui aussi de poster la réponse :p bien joué moi j'ai oublié le cas de f(x)=-1 | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Jeu 16 Jan 2014, 18:30 Jeu 16 Jan 2014, 18:30 | |
| dans ce cas f(x)=-1 n'est pas une solution alors elle est éliminée | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Jeu 16 Jan 2014, 18:34 Jeu 16 Jan 2014, 18:34 | |
| SOLUTION exo2
en encadrant f(x) entre x-1=<f(x) et f(x)=<x-1
on en déduit que f(x)=x-1.
j'attends votre confirmation pour poster le 3eme | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Jeu 16 Jan 2014, 18:37 Jeu 16 Jan 2014, 18:37 | |
| - L-W-P a écrit:
- dans ce cas f(x)=-1 n'est pas une solution alors elle est éliminée
J'ai mentionné ce détail dans ma démo | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Jeu 16 Jan 2014, 18:38 Jeu 16 Jan 2014, 18:38 | |
| - legend-crush a écrit:
- L-W-P a écrit:
- dans ce cas f(x)=-1 n'est pas une solution alors elle est éliminée
J'ai mentionné ce détail dans ma démo pardon j'ai pas lu votre démarche. | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Jeu 16 Jan 2014, 18:40 Jeu 16 Jan 2014, 18:40 | |
| - L-W-P a écrit:
- dans ce cas f(x)=-1 n'est pas une solution alors elle est éliminée
oui oui je sais c'est seulement une notation | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Jeu 16 Jan 2014, 18:41 Jeu 16 Jan 2014, 18:41 | |
| car j'ai fais f²(x)=1=> f(x)=1 mais les solutions sont 1 et -1 puis on conclur...
pour comprendre bien la solution | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Ven 17 Jan 2014, 15:52 Ven 17 Jan 2014, 15:52 | |
| exo 3
trouver toutes foctions de Z----Z AVEC f(0)=1 et
pour tous n appartient à Z on a
f(f(n))=f(f(n+2)+2)=n | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Ven 17 Jan 2014, 20:44 Ven 17 Jan 2014, 20:44 | |
| il parait bien que f est injective, en effet f(n)=f(m) --> fof(n)=fof(m) --> m=n
On demontre par réccurence que f(n)=1-n pour tout n de N. pour n=0 c'est vrai ( et pour 1 aussi)
HR: soit n de N, on suppose que l'assertion est juste jusqu'a n.
on démontre pour n+1: f(f(n+1)+2)=f(f(n-1)) --> f(n+1)=f(n-1)-2= 1-n+1-2=-n=1-(n+1)
donc f(n)=1-n pour tout n de N
On démontre a présent pour Z-, soit m de Z-:
f(f(m))=m=1-(1-m) =f(1-m) --> f(m)= 1-m ( vu l'injectivité de f)
Conclusion f(n)=1-n
Sauf Erreur, Je poste? | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Sam 18 Jan 2014, 07:24 Sam 18 Jan 2014, 07:24 | |
| | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Sam 18 Jan 2014, 10:36 Sam 18 Jan 2014, 10:36 | |
| Ok Exercice 4:trouver toutes les fonctions 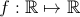 tel que:  pour tout 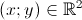 | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Sam 18 Jan 2014, 13:57 Sam 18 Jan 2014, 13:57 | |
| | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Sam 18 Jan 2014, 20:40 Sam 18 Jan 2014, 20:40 | |
| la solution n'est pas complete mais bon.
J'admet que f(0)=0 (ce qui est vrai et que je n'ai pas demontré)
P(0;x) --> f(f(x))=x
P(f(x);y) --> f(f(x)f(f(x))+y)=(f(f(x)))²+y --> f(xf(x)+y)=x²+y
Donc: x²+y=f(x)²+y --> f(x)²=x²
De ce fait: f(x)=x ou f(x)=-x
si quelqu'un a une idee pour f(0) , elle est la bienvenue.
Amicalement. | |
|
  | |
charaf_X
Débutant
 Nombre de messages : 4 Nombre de messages : 4
Age : 28
Localisation : Tanger
Date d'inscription : 22/12/2013
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Sam 18 Jan 2014, 22:45 Sam 18 Jan 2014, 22:45 | |
| pour 0 j'ai pensé à montrer que f elle est injective et ceci par f(-xf(x)-f(y))=(-f(x))^2 +y =(f(x))^2+y = f(xf(x)+f(y)) dés lors la fonction f est injective ; mais je ne sais pas trop si j'ai le droit de procéder ainsi    | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Dim 19 Jan 2014, 01:47 Dim 19 Jan 2014, 01:47 | |
| - charaf_X a écrit:
- pour 0 j'ai pensé à montrer que f elle est injective et ceci par
f(-xf(x)-f(y))=(-f(x))^2 +y =(f(x))^2+y = f(xf(x)+f(y))
dés lors la fonction f est injective ; mais je ne sais pas trop si j'ai le droit de procéder ainsi    f est bijective car P(0,x)=>f(f(x))=x+f²(0) alors il existe un c de R tel que f(c)=0 P(c,0)=>f(f(0))=0 et P(0,0)=>f(f(0))=f²(0) alors f(0)=0 | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Dim 19 Jan 2014, 01:58 Dim 19 Jan 2014, 01:58 | |
| - legend-crush a écrit:
- la solution n'est pas complete mais bon.
J'admet que f(0)=0 (ce qui est vrai et que je n'ai pas demontré)
P(0;x) --> f(f(x))=x
P(f(x);y) --> f(f(x)f(f(x))+y)=(f(f(x)))²+y --> f(xf(x)+y)=x²+y
Donc: x²+y=f(x)²+y --> f(x)²=x²
De ce fait: f(x)=x ou f(x)=-x
si quelqu'un a une idee pour f(0) , elle est la bienvenue.
Amicalement. Ce passage n'est pas permis. | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Dim 19 Jan 2014, 02:24 Dim 19 Jan 2014, 02:24 | |
| Il faudra distinguer deux cas.
Puisque f²(x)=x², soit f(1)=1 soit f(1)=-1 .
***f(1)=1
On prend x=1, y=x dans L'EF de départ pour trouver f(f(x)+1)=x+1 donc (x+1)²=f²(f(x)+1)=(f(x)+1)²
Ainsi f²(x)+2f(x)=x²+2x ==> f(x)=x
***f(1)=-1
Avec la même méthode nous aboutissons à f(x)=-x.
Réciproquement x->x et x-> -x sont les deux solutions de l'équation de départ. | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Dim 19 Jan 2014, 10:55 Dim 19 Jan 2014, 10:55 | |
| Exercice 6: Trouver toutes les fonctions strictement monotones de N vers N, tel que pour tous n de N, on ait: 
Dernière édition par legend-crush le Dim 19 Jan 2014, 14:51, édité 1 fois | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Dim 19 Jan 2014, 13:42 Dim 19 Jan 2014, 13:42 | |
| - legend-crush a écrit:
- Exercice 6:
Trouver toutes les fonctions de N vers N, tel que pour tous n de N, on ait:
 Bonjour, d'où avez-vous eu ce problème Legend-crush ? | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Dim 19 Jan 2014, 14:14 Dim 19 Jan 2014, 14:14 | |
| - Humber a écrit:
Bonjour, d'où avez-vous eu ce problème Legend-crush ? http://www.imosuisse.ch/skripte/algebra/fr-funktionalgleichungen_aufgaben.pdf dernière page  | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Dim 19 Jan 2014, 14:37 Dim 19 Jan 2014, 14:37 | |
| Je me doutais bien qu'il manquait quelque chose. Veillez à copier l'énoncé comme il est s'il vous plaît.  | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  Dim 19 Jan 2014, 14:52 Dim 19 Jan 2014, 14:52 | |
| Voila, c'est edité, desolé pour l'erreur . | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Monde des équations fonctionnelles Sujet: Re: Monde des équations fonctionnelles  | |
| |
|
  | |
| | Monde des équations fonctionnelles |  |
|
