Monde des équations fonctionnelles

peut etre. mais ce n est pas la seule solution.
la reponse est :

Spoiler:

Notre solution, à Legend-Crush et moi (je me l'approprie aussi car je suis arrivé au même résultat), n'est pas fausse.

Enfin, x = 1 ; y => f(f(f(1))) f(f(y))= 1 * y = y ce qui fait que fof(x) = x => fofof(x) = f(x) (deux nombres égaux ont une même image...)

La ligne est correcte. Enfin...C'est ce que je crois. A moins que Legend-Crush et moi ne savons plus notre algèbre, là, c'est différent

tu sais c est pas a moi de dire ca....

Spoiler:

Il y avait donc une faute dans l'enonce de l'exercice que tu as propose.Il fallait ecrire
Trouver toutes les valeurs possibles de f(30) tel que f soit une fonction de N vers N qui verifie :
f(x)<=x^2 et f(f(f(x))*f(f(y)))=xy.

je ne vois pas trop la difference avec ce que j ai ecris....

Dans le dessein de réanimer ce sujet assez intéressant je poste une équation fonctionnelle quoique qu'elle soit classique mais elle demeure utile.
Exo 
    (A):    f(x+y)=f(x)*f(y)   ( quelque soient x,y de IR)
1) monter que si f est dérivable en 0 elle est continue sur IR.
2) déterminer toutes fonctions soumettent à cette propriété (A).

Dans le même dessein que vous, je ne traiterai que la première partie de l'exercice pour laisser aux autres visiteurs de la page la possibilité de participer:

On a si f est dérivable en 0, donc elle y est continue.

On a aussi: f(0) = f(0+0) = f(0) * f(0) <--> f(0) * (f(0) - 1) <--> f(0) = 0 ou f(0) = 1 .

a - Si f(0) = 0
Pour tout x de IR on a : f(x) = f(x+0) = f(x) * f(0) = 0 , donc f est la fonction nulle qui est continue sur IR .

b - Si f(0) = 1

Pour tout x de IR et en posant x = x0 + h, on a:
lim     f(x) = lim f(x0+h) = lim f(x0) * f(h) = f(x0) * lim f(h) = f(x0) * f(0)
x-->x0         h-->0            h-->0                             h-->0
car f est continue en 0 et donc lim f(h) = f(0)
                                             h-->0
donc lim f(x) = f(x0) * f(0) = f(x0); donc f est continue en x0 et par suite
        x-->x0
elle est continue sur IR.

Donc si f est dérivable en 0 alors elle est continue sur IR .

Mr ayemanmaysae je préféré que tu poste la solution du 2) pour ne pas ralentir le travail surtout que ces derniers jours les membres ne sont pas nombreux, par conséquent la possibilité que quelqu'un poste la solution diminuera.

La meilleure solution que j'ai trouvée est sous forme de cours: elle aboutit à ce que la fonction exponentielle est l'unique solution.

Vous trouverez ce cours en suivant ce lien: http://math.univ-lyon1.fr/capes/IMG/pdf/exponentielle.pdf .

Merci aymanemaysae pour ce document à toi de poster ou quelqu'un d'autre le fera.

Je relance ce sujet :
Trouver ttes les fonctions R --- R qui verifient :
f(x²-y²)=f(x)²-f(y)²
Bonne chance.

P(0;0) : f(0)=0
P(x;0): f(x²)=f(x)² (>0) ==> f(x)>0 pour tout x>0
Aussi Clairement f est impair.
Sur R+ : x>y => x²>y² => x²-y²>0 => f(x²-y²)>0 => f(x)²-f(y )²>0 => f(x)>f(y )
Ce qui fait que f est croissante sur R+ et donc sur R
Mtn On a P(x;y): f(x²-y²)=f(x²)-f(y²)
==> P(rac(x);rac(y ) ) : f(x-y )=f(x)-f(y ) => on pose k=x-y
=> f(k)=f(k+y)-f(y ) => f(k+y )=f(k)+f(y ) ==> equation de caushy sur R+ pour eviter des problème puis déduire sur R-
alors f(x)=ax on remplace dans l'equation principale => ax²-ay²=a²x²-a²y²
=> a=1 ou a=0
Finalement les seules solutions de l'equation sont f(x)=0 et f(x)=x

Bravo , L-C , a toi de proposer une Ef , chi 7aja mlii7a laykhlik ^_^

Find all functions f : R → R that satisfy
f(m+ nf(m)) = f(m) + mf(n)
for all m and n.

http://www.artofproblemsolving.com/Forum/viewtopic.php?t=326890

J'ajoute du chocolat suisse  
Trouver ttes les fonctions de R+ vers R+ telles que avec .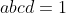
ENJOY

posons a=b=c=d=1
4f(1)^2=4 ==>f(1)=1
a=b=1 et cd=1
2 (f(c)+f(d) )=2 (c+d) ==> f(c)+f(d)=c+d ==> f(x)+f(1/x) =x +1/x
a=c=1 ,bd=1
(1+f(b) )(1+f(c) ) =(1+b)(1+c) ==>f(b)f(c)=bc ==> f(x)f(1/x)=1

f(x)+f(1/x) =x +1/x et f(x)f(1/x)=1 ==> ( f(x)-f(1/x) )^2= (x-1/x)^2
==> f(x)-f(1/x) = x-1/x ==> f(x)=x
ou  f(x)-f(1/x) = 1/x -x ==> f(x)=1/x

donc f(x)=x ou 1/x
clairement f(x)=x et f(x)=1/x sont des solutions
maintenant soit a b c et d tels que f(a)=a , f(b)=b ,f(c)=1/c f(d) =1/d
(f(a) +f(b))(f(c)+f(d) )=(a+b)(c+d)/ab=(a+b)(c+d) ==> ab=cd=1
(f(a)+f(c))(f(b)+f(d) )=(a +1/c)(b+1/d)=(a+c)(b+d)
==>b/c +a/d =bc +ad=db+ac ==> b(d-c)=a(d-c)==>a=b=1 ou d=c=1

maintenant soit a b c et d tels que f(a)=a , f(b)=b ,f(c)=c f(d) =1/d
(a+b)(c+1/d)=(a+b)(c+d) ==>b/d +a/d =bd+ad ==>d=1

le dernier cas: soit a b c et d tels que f(a)=a , f(b)=1/b ,f(c)=1/c f(d) =1/d
(a+1/b)(1/c +1/d) =(a+b)(c+d)
(a+1/c)(1/b +1/d) =(a+c)(b+d)
on montre par la meme methode que a=1
(je suis pressé, m excuse )
du coup , f(x)=x et f(x)=1/x sont les seules solutions

si c'est correct, je me permet de poser l'exercice suivant

Soit f : N --> R ayant la propriete suivante: pour tout n > 1 il existe un
diviseur premier p de n avec f(n) = f(n/p) − f(p). De plus, f(2001) = 1. Trouver
f(2002).

2001=23*29*3 et 2002=11*7*13*2
f(2001)=f(2001/p)-f(p)  *    (p={23 ou 29 ou 3})
et encore 2001/p n'est pas premier 
f(2001/p)=f(2001/p*q)-f(q) **(q prend l'une des deux valeurs restantes(23ou 29)ou(23ou3)ou(29ou3))
2001/pq sera premier d’où f(2001/pq)=f(1)-f(2001/pq)---> f(2001/pq)=f(1)/2 et f(p)=f(1)/2 et f(q)=f(1)/2  ***

selon * et ** et *** 1=f(1)/2-f(1)/2-f(1)/2 ce qui fait que f(1)=-2
f(2002)=f(2002/m)-f(m)       ( m={11 ou 7 ou 13 ou 2})
2002/m pas premier
f(2002/m)=f(2002/mn)-f(n)    (n prend l'une des valeurs restantes de m)
f(2002/mn)=f(2002/m*n*s)-f(s)  (s prend l'une des valeurs restantes de n)
f(2002/mns)=f(2002/mnsr)-f(r)    ( r prend la valeur restante)
2002/mnsr est premier d'où f(2002/mnsr)=f(1)/2

f(2002)=f(1)/2-f(1)/2-f(1)/2-f(1)/2-f(1)/2=6
f(2002)=6
Sauf erreur

L-W-P a toi de proposer une EF

la fonction f(x,y) satisfait les équations suivantes pour tous x,y>=0:
f(0;y)=y+1
f(x+1;0)=f(x;1)
f(x+1;y+1)=f(x;f(x+1,y))
déterminer f(4;1981)