Pour vous !

bonne chance  

voici la suite  ... enjoy   

solution exo 1
1) a)

et puisque on va calculer la limite auprès de 1+ on va prendre x>=-2 et encore x+2>=0
après une factorisation avec (x-1) et simplifier on aura


b) d'où on peut dériver f en 1 et f est continue en 1
2)


f n'est pas dérivable en -2

Sauf erreur de calcul

Solution exo 2


=-1



4)

5) utiliser l’hôpital
la dérivé de (x+x^2+...+x^n)-n est x+2x+..+nx^(n-1)
et la dérivé de (2-x)^(n)-1 est n(2-x)^(n-1)
en remplaçant par 1
on trouvera que la limite est (n+1)/2
SAUF ERREUR

solution exo 3
 1)

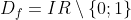
2)

3) puisque (x^2-x)^2 est toujours positive il suffit d'étudier le signe (2x-1)
f' est positive dans l'intervalle [1/2,+inf[
f' est négative dans l'intervalle ]-inf,1/2]
d'où
f est croissante sur [1/2,+inf[
f est décroissante sur ]-inf,1/2]
la valeur maximale de f est 9  (*)
4)b) pour que sin^2+cos^2=1 on doit avoir au moins l'un d'eux cos^2>=1/2  (on peut la démontrer par l'absurde)
et posant x=cos^2  alors 1-x=sin^2
et puis on utilise (*) pour déduire que  (puisque cos^2>=1/2)

oui c facile comme un DS vos réponse sont justes    et le gout de ce DS c'est les deuxx bonus

merci pour partager ce document, mais est ce  dans exercice2 5) n la puissance ou le degré de dérivation.

c la puissance