Condition suffisante de convexité

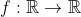Soit une $Condition suffisante de convexité Gif$ une fonction continue, telle que pour 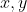$Condition suffisante de convexité Gif$ réels, $Condition suffisante de convexité Gif$
montrer que $Condition suffisante de convexité Gif$ est convexe

D={m/2^n : m et n entiers>=0 et m=<2^n} est dense dans [0,1]
l'hypothèse ==> f(m/2^n.x +(1-m/2^n).y)=<m/2^n.f(x) +(1-m/2^n).f(y)
par continuité, f(t.x+(1-t).y)=<t.f(x)+(1-t).f(y)

Généralisation:

Soit une 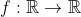$Condition suffisante de convexité Gif$ une fonction continue, telle que pour tous 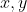$Condition suffisante de convexité Gif$ réels,
il existe 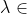$Condition suffisante de convexité Gif$ [0,1] : $Condition suffisante de convexité Gif$
montrer que $Condition suffisante de convexité Gif$ est convexe

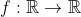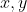Mohammed_Lahlou a écrit:: Soit une $Condition suffisante de convexité Gif$ une fonction continue, telle que pour $Condition suffisante de convexité Gif$ réels, $Condition suffisante de convexité Gif$
montrer que $Condition suffisante de convexité Gif$ est convexe

Je propose une solution différente:
On définit l'intervalle 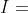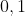$Condition suffisante de convexité Gif$ ] $Condition suffisante de convexité Gif$ [ pour des raisons d'écriture en Latex.
On veut montrer que $Condition suffisante de convexité Gif$ .
Soient $Condition suffisante de convexité Gif$ et $Condition suffisante de convexité Gif$ deux réels différents tels que: 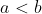$Condition suffisante de convexité Gif$ , et soit 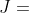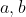$Condition suffisante de convexité Gif$ ] $Condition suffisante de convexité Gif$ [.
On va montrer que $Condition suffisante de convexité Gif$ .
Quitte à remplacer la fonction $Condition suffisante de convexité Gif$ par la fonction $Condition suffisante de convexité Gif$ , on peut supposer que $Condition suffisante de convexité Gif$ et on doit démontrer que $Condition suffisante de convexité Gif$ .
Cela se démontre de proche en proche, en prenant passant toujours par la moitié d'un segment dont les extrémités ont des images négatives.
On a $Condition suffisante de convexité Gif$ . On fait de même avec 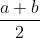$Condition suffisante de convexité Gif$ et $Condition suffisante de convexité Gif$ et avec 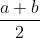$Condition suffisante de convexité Gif$ et $Condition suffisante de convexité Gif$ .
Et on itère ce processus qui couvre tout l'intervalle 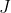$Condition suffisante de convexité Gif$ pour conclure.
Sauf erreurs, qui ont de fortes chances d'exister.

abdelbaki.attioui a écrit:: Généralisation:

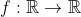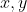Soit une $Condition suffisante de convexité Gif$ une fonction continue, telle que pour tous $Condition suffisante de convexité Gif$ réels,
il existe 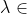$Condition suffisante de convexité Gif$ [0,1] : $Condition suffisante de convexité Gif$
montrer que $Condition suffisante de convexité Gif$ est convexe

Soient a et b des réels , a<b
On pose g(t)= f( a+t(b-a))-f(a)-t(f(b)-f(a)) pour t dans [0,1]
Il s'agit de montrer que g=<0 sur [0,1]
g continue sur [0,1] alors Max g sur [0,1] =g(u) avec u dans [0,1] .
Si 0<u<1. Par hypothèse et pour n assez grand
il existe u-1/n<t_n<u +1/n: g(t_n)=<0 ==> g(u)=<0
Si u=0 ou 1 , g(u)=0
D'où le résultat

abdelbaki.attioui a écrit:: Généralisation:
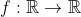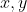Soit une $Condition suffisante de convexité Gif$ une fonction continue, telle que pour tous $Condition suffisante de convexité Gif$ réels,
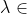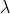il existe $Condition suffisante de convexité Gif$ [0,1] : $Condition suffisante de convexité Gif$
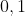montrer que $Condition suffisante de convexité Gif$ est convexe

La solution que vous avez apporté est très belle et astucieuse.
Et je pense que la généralisation doit être faite dans le sens suivant:
Il existe $Condition suffisante de convexité Gif$ appartenant à ] $Condition suffisante de convexité Gif$ [ tel que: $Condition suffisante de convexité Gif.latex?(\forall x,y\in\mathbb{R}): f(\lambda.x+(1-\lambda).y)\le\lambda.f(x)+(1-\lambda)$ .

nmo a écrit:

abdelbaki.attioui a écrit:: Généralisation:
Soit une $Condition suffisante de convexité Gif$ une fonction continue, telle que pour tous $Condition suffisante de convexité Gif$ réels,
il existe $Condition suffisante de convexité Gif$ [0,1] : $Condition suffisante de convexité Gif$
montrer que $Condition suffisante de convexité Gif$ est convexe

La solution que vous avez apporté est très belle et astucieuse.
Et je pense que la généralisation doit être faite dans le sens suivant:
Il existe $Condition suffisante de convexité Gif$ appartenant à ] $Condition suffisante de convexité Gif$ [ tel que: $Condition suffisante de convexité Gif.latex?(\forall x,y\in\mathbb{R}): f(\lambda.x+(1-\lambda).y)\le\lambda.f(x)+(1-\lambda)$ .

Merci nmo pour le compliment
La généralisation que j'ai proposé est plus forte vu que l'hypothèse: chaque couple a son $Condition suffisante de convexité Gif$ est plus faible qu'il y a un $Condition suffisante de convexité Gif$ pour tous les couples. Mais enfin de compte les deux hypothèses sont équivalentes à la convexité donc eux mêmes sont équivalentes

» ensembles...condition nécéssaire et suffisante...urgent
» une condition pour que cette suite converge
» convexité
» trouver une condition sur a
» convexité