exo!! paramètre et E(x)

exo 1:
est ce que qu'on peut choisir m pour que la solution de l’équation soit dans : [1;2]
m²(x-l(1+2m)l)=x-rac(1+4m+4m²)
exo 2:
soit S ensemble de solution de : x²+xE(x)-1=0
1-prouve que qls x de R: xE(x)>=0 (facile)
2-déduire que : S appartient a [-1;1]
3-prouve que Sn[0;1]=ensemble vide
4-prouve que x²-x-1=(x-(1-rac(5))/2)(x-(1+rac(5))/2) puis trouve S

aminesm a écrit:

exo 1:
est ce que qu'on peut choisir m pour que la solution de l’équation soit dans : [1;2]
m²(x-l(1+2m)l)=x-rac(1+4m+4m²)

On a .
Donc l'équation devient: .
Si , on aura et ainsi .
On veut que soit dans [], alors .
Ce qui donne ou bien .
Soit ou bien .
D'où ou bien .
Ce sont alors les valeurs de qu'on cherche.
Sauf erreurs.

aminesm a écrit:

exo 2:
soit S ensemble de solution de : x²+xE(x)-1=0
1-prouve que qls x de R: xE(x)>=0 (facile)
2-déduire que  : S appartient a [-1;1]
3-prouve que Sn[0;1]=ensemble vide
4-prouve que x²-x-1=(x-(1-rac(5))/2)(x-(1+rac(5))/2) puis trouve S

Je propose une solution:
1- Soit .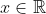
Il existe un entier de 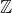et un réel de [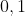[ tel que: .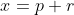
L'inégalité s'écrit .
Si , tout est bon, l'inégalité est évidente.
Sinon, ou bien .
On écrit l'inégalité sous la forme: .
Et cela est vrai, car on a et .
Avec égalité si et seulement si 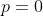, soit .
Dans tous les cas, on a prouvé le résultat.

2- L'équation équivaut à .
Et puisque , il vient que ou encore que [].

3- On distingue deux cas:
* Si est un élément de [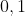[, alors .
L'équation devient , ce qui contredit le fait que [[.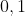
* Si 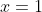, l'équation n'est pas vérifiée trivialement.

4- Si est solution, alors est un élément de [[ ce qui donne que .
L'équation devient: 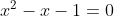, soit ou bien .
D'où .
Donc ou bien . Soit ou bien .
Mais, puisque [[ alors .
Finalement, .

Sauf erreurs.