- abraha_11 a écrit:
- Bonjour.
Montrer que: ((1-1/n^2)^n )*(1+1/n) < 1
J'imagine qu'on veut démontrer l'inégalité pour tout entier non nul

.
L'inégalité est trivialement vérifiée pour
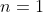
. On s'intéresse désormais au cas
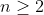
.
L'inégalité se réécrit
 : \Big(\frac{n+1}{n}\Big)^{n+1}<\Big(\frac{n}{n-1}\Big)^{n})
.
Ou, de manière équivalent,
 : (n+1)\ln(\frac{n+1}{n})<n\ln(\frac{n}{n-1}))
.
On définit la fonction

par
 : f(x) = x\ln(\frac{x}{x-1}))
.
Cette fonction est dérivable, et on a
 : f'(x) = \ln(\frac{x}{x-1})-\frac{1}{x-1})
.
Par ailleurs, il est connu (il est facile à démontrer) que
 : \ln(t) < t - 1)
.
Cette inégalité implique que
 : f'(x) < 0)
(En prenant
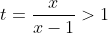
).
Par conséquent, la fonction

est bien décroissante sur ]
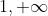
[.
On a donc
 : f(n+1) < f(n))
ou bien
 :(n+1)\ln(\frac{n+1}{n})<n\ln(\frac{n}{n-1}))
.
Sauf erreurs.
