DEVOIR n1 OLYMPIADE TRONC COMMUN 24 NOVEMBRE 2017

Bonjour ;

Exercice n° 1 .

1/(xy) + 1/(yz) + 1/(zx) = z/(xyz) + x/(xyz) + y/(xyz) = (x + y + z)/(xyz) = 2 ;
donc : x + y + z = 2xyz .

1/x + 1/y + 1/z = (yz)/(xyz) + (xz)/(xyz) + (xy)/(xyz) = (xy + yz + zx)/(xyz) = V2 .

On a donc : (x + y + z)/(xy + yz + zx) = (2xyz)/(V2 xyz) = V2 .

Exercice n° 2 .

Soit (A;AB;AD) un repère normé ,
donc on a : A(0;0) , B(1;0) , C(1,1) , D(0;1) et I(1;1/2) .

Soit H(u;v) ,
donc le vecteur DH est : DH(u;v-1) , et le vecteur AI est : AI(1;1/2) .

Comme les droites (DH) et (AI) sont perpendiculaires ,
donc : u + 1/2(v - 1) = 0 ,
donc : v = 1 - 2u ,
donc : H(u;1 - 2u) .

L'équation réduite de la droite (AI) est : y = 1/2 x ,
et la droite réduite de la droite (DH) est : u = - 2x + 1 .

Comme H(u;1 - 2u) est le point d'intersection des droites (AI) et (DH) ,
donc on a : 1/2 x = - 2x + 1 ,
donc : x = 2/5 et y = 1/5 ,
donc : H(2/5 ; 1/5) .

Enfin on a :
CH² = (2/5 - 1)² + (1/5 - 1)² = 1 = CD² ,
donc : CH = CD .

Bonjour ;

Exercice n° 3 .

Je note Z(x) la racine carré de x , avec x un nombre réel positif .

1)

ax + b/x - 2Z(ab) = Z²(ax) + Z²(b/x) - 2Z(ax * b/x) = (Z(ax) - Z(b/x))² >= 0 ,
donc : ax + b/x >= 2Z(ab) .

2)

2(xy/z + yz/x + zx/y) = (y/z)x + (yz)/x + (z/x)y + (zx)/y + (x/y)z + (xy)/z
>= 2Z(y/z * yz) + 2Z(z/x * zx) + 2Z(x/y * xy)
= 2y + 2 z + 2x ;

donc :

xy/z + yz/x + zx/y >= x + y + z .

Une autre méthode est comme suit :

xy/z + yz/x + zx/y >= x + y + z
<==> x²y²/xyz + y²z²/xyz + z²x²/xyz >= x + y + z
<==> x²y² + y²z² + z²x² >= xyz(x + y + z)
<==> x²y² + y²z² + z²x² >= x²y²z²(1/(yz) + 1/(zx) + 1/(xy))
<==> 1/z² + 1/x² + 1/y² >= 1/(yz) + 1/(zx) + 1/(xy)
<==> (1/z² + 1/x²) +(1/x² + 1/y²) + (1/y² + 1/z²) >= 2/(yz) + 2/(zx) + 2/(xy)
<==> (1/z² + 1/x² - 2/(zx)) +(1/x² + 1/y² - 2/(xy)) + (1/y² + 1/z² - 2/(yz)) >= 0
<==> (1/z - 1/x)² + (1/x - 1/y)² + (1/y - 1/z)² >= 0 : proposition vraie ,
donc la proposition : xy/z + yz/x + zx/y >= x + y + z est aussi vraie .

Cas d'égalité :

xy/z + yz/x + zx/y = x + y + z
<==> (1/z - 1/x)² + (1/x - 1/y)² + (1/y - 1/z)² = 0
<==> (1/z - 1/x)² = 0 et (1/x - 1/y)² = 0 et (1/y - 1/z)² = 0
<==> 1/z - 1/x = 0 et 1/x - 1/y = 0 et 1/y - 1/z = 0
<==> 1/z = 1/x et 1/x = 1/y et 1/y = 1/z
<==> x = y = z .

Exercice n° 4 .

Les coordonnées du milieu d'un segment sont des nombres entiers si et seulement si
les coordonnées de ses deux extrémités sont aussi des nombres entiers.

Quand on choisit un point, il appartient à l'une des quatre familles ci-dessous :
- les points d'abscisse et d'ordonnée paires;
- les points d'abscisse paire et d'ordonnée impaire;
- les points d'abscisse impaire et d'ordonnée paire;
- les points d'abscisse et d'ordonnée impaires;
Si on choisit cinq points , alors, forcément deux au moins vont se retrouver dans la même famille (car il y a 5 points et 4 familles, donc pas assez de familles pour que chaque points soit séparé de tous les autres - c'est ce qu'on appelle le principe des tiroirs).
Alors pour ces deux points, comme leurs abscisses x1 et x2 sont de même parité, l'abscisse de leur milieu (la moyenne de x1 et x2) est un nombre entier. De même, l'ordonnée du milieu est un nombre entier.

aymanemaysae a écrit:

Exercice n° 4 .

Les coordonnées du milieu d'un segment sont des nombres entiers si et seulement si
les coordonnées de ses deux extrémités sont aussi des nombres entiers.

Quand on choisit un point, il appartient à l'une des quatre familles ci-dessous :
   - les points d'abscisse et d'ordonnée paires;
   - les points d'abscisse paire et d'ordonnée impaire;
   - les points d'abscisse impaire et d'ordonnée paire;
   - les points d'abscisse et d'ordonnée impaires;
Si on choisit cinq points , alors, forcément deux au moins vont se retrouver dans la même famille (car il y a 5 points et 4 familles, donc pas assez de familles pour que chaque points soit séparé de tous les autres - c'est ce qu'on appelle le principe des tiroirs).
Alors pour ces deux points, comme leurs abscisses x1 et x2 sont de même parité, l'abscisse de leur milieu (la moyenne de x1 et x2) est un nombre entier. De même, l'ordonnée du milieu est un nombre entier.

En générale ce qui est en rouge est faux, prend par exemple X(2/3,-4/5) and Y(4/3,14/5) alors les coordonnées du Z le milieu de [XY] sont Z(1,1)

Voici une autre solution pour l'exercice 3 :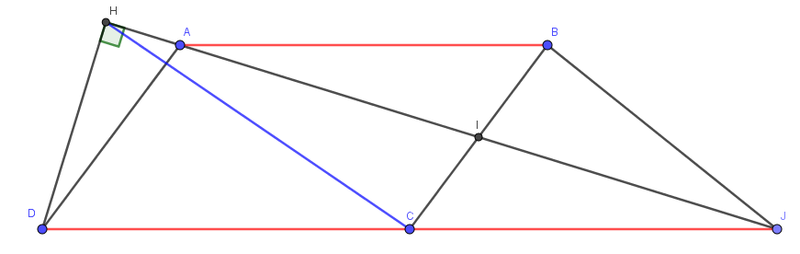

Soit J=intersection du (AI) et (DC), Dans le quadrilatère ABJC (CJ)//(AB) et I le milieu [BC] d’après Thales on a IA/IJ=IB/IC=1 donc I le milieu du [AJ] aussi, alors ABJC est un parallélogramme i.e CJ=BA=CD et alors C le milieu du [DJ], donc DHJ est un triangle rectangle en H et C le milieu de [DJ] alors CH=CJ=CD.

Bonsoir ;

je rectifie :

aymanemaysae a écrit:

Les coordonnées du milieu d'un segment sont des nombres entiers naturels si et seulement si
les coordonnées de ses deux extrémités sont aussi des nombres entiers naturels .

aymanemaysae a écrit:

Bonsoir ;

je rectifie :

aymanemaysae a écrit:

Les coordonnées du milieu d'un segment sont des nombres entiers si et seulement si
les coordonnées de ses deux extrémités sont aussi des nombres entiers .

Prend A(2x,2y) et B(2x',2y') donc I(x+x',y+y') (I le milieu du [AB])

Vous avez dit que (x+x',y+y')∈ℕ²⇔2x,2y,2x',2y'∈ℕ mais ça est faut

Pour la 1er implication (x+x',y+y')∈ℕ²⇒2x,2y,2x',2y'∈ℕ prend comme contre exemple x+x'=y+y'=1 et x=1/3,x'=2/3,y=-2/5 et y'=7/5 mais 2x,2y,2x',2y'∉ℕ

Pour la 2eme 2x,2y,2x',2y'∈ℕ⇒(x+x',y+y')∈ℕ² prend 2x=1,2y=3,2x'=2 et 2y'=4 on a x+x'=3/2∉ℕ et y+y'=7/2∉ℕ.

Bonjour ;

suite aux remarques de "elmrini" , le théorème que j'ai énoncé est faux , néanmoins , je pense que le reste est juste .