| | limite d'une suite définie par tan |  |
|
|
| Auteur | Message |
|---|
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: limite d'une suite définie par tan Sujet: limite d'une suite définie par tan  Mar 20 Nov 2018, 15:07 Mar 20 Nov 2018, 15:07 | |
| (Un) une suite définie par: Un.tan(P/2.Un)=P/2n
sachant que limUn=0 et (Un) est ds [0,1] calculer: lim rac(n).Un
Dernière édition par madani le Lun 26 Nov 2018, 19:47, édité 1 fois | |
|
  | |
Litorus
Habitué

 Nombre de messages : 27 Nombre de messages : 27
Age : 27
Date d'inscription : 07/01/2014
 |  Sujet: Re: limite d'une suite définie par tan Sujet: Re: limite d'une suite définie par tan  Mer 21 Nov 2018, 02:55 Mer 21 Nov 2018, 02:55 | |
| Bonsoir Madani, 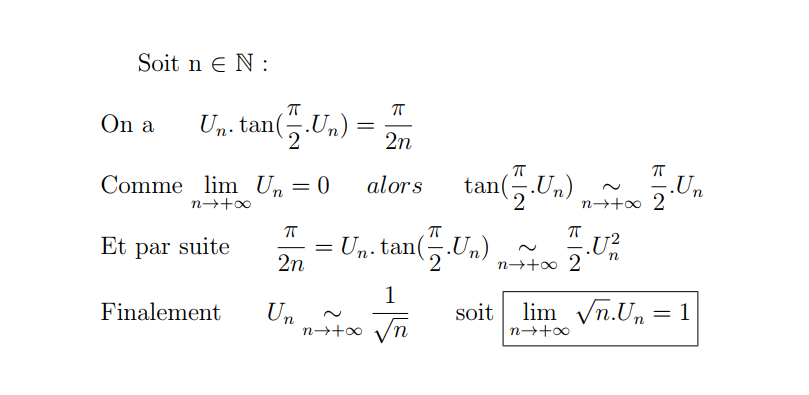 | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: limite d'une suite définie par tan Sujet: Re: limite d'une suite définie par tan  Mer 21 Nov 2018, 10:16 Mer 21 Nov 2018, 10:16 | |
| bjr
si un élève de 2BSM donne cette réponse au bac il aura certainement un zéro ! non ? | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: limite d'une suite définie par tan Sujet: Re: limite d'une suite définie par tan  Mer 21 Nov 2018, 10:24 Mer 21 Nov 2018, 10:24 | |
| BJR au Forum.
Aid Moubarak Said .
BJR Mr MADANI , les souvenirs de la Faculté des Sciences de Rabat sont toujours Vivaces !!!!
Il y a un point d' ombre à la dernière ligne de la démo de Litorus .....
Du résultat :
Lim n.(Un)^2 =1 quand n tend vers + infini
Ne permet pas à priori de conclure que :
rac(n).Un tend vers 1 ds ces mêmes conditions !!!
Au final : quel est le signe de Un ????
Ou du moins à partir d' un certain rang ???? | |
|
  | |
Litorus
Habitué

 Nombre de messages : 27 Nombre de messages : 27
Age : 27
Date d'inscription : 07/01/2014
 |  Sujet: Re: limite d'une suite définie par tan Sujet: Re: limite d'une suite définie par tan  Mer 21 Nov 2018, 15:12 Mer 21 Nov 2018, 15:12 | |
| Bonjour,
Je n'ai pas fait attention au signe de Un. Sinon j'arrive pas à avoir plus de détails sur la suite Un de juste son expression par la tangente. Dois-je distinguer les cas ? | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: limite d'une suite définie par tan Sujet: Re: limite d'une suite définie par tan  Mer 21 Nov 2018, 15:51 Mer 21 Nov 2018, 15:51 | |
| Aid mobarek Said mon prof Lhassane ! effectivement j ai du oublier de signaler que (Un) est ds [0.1]!
Dernière édition par madani le Ven 23 Nov 2018, 18:32, édité 3 fois | |
|
  | |
Litorus
Habitué

 Nombre de messages : 27 Nombre de messages : 27
Age : 27
Date d'inscription : 07/01/2014
 |  Sujet: Re: limite d'une suite définie par tan Sujet: Re: limite d'une suite définie par tan  Mer 21 Nov 2018, 17:02 Mer 21 Nov 2018, 17:02 | |
| Quelle surprise vous étiez l'un des étudiants de M.Oeil de Lynx ! | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: limite d'une suite définie par tan Sujet: Re: limite d'une suite définie par tan  Ven 23 Nov 2018, 18:26 Ven 23 Nov 2018, 18:26 | |
| - Litorus a écrit:
- Quelle surprise vous étiez l'un des étudiants de M.Oeil de Lynx !
effectivement mr lhassane était prof de ma promotion a la fct Mhd5 a rabat et j en suis ravi !!! mais n abandonne ps ton raisonnement tu peux tjrs le réussir en transformant tes expressions équivalentes a des inégalités adéquates et bn chance !!! | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: limite d'une suite définie par tan Sujet: Re: limite d'une suite définie par tan  Sam 15 Déc 2018, 20:45 Sam 15 Déc 2018, 20:45 | |
| une autre façon de l utilisation des fcts équivalentes c est la notion de limite :
on a lim Un=0 dc :
lim [tan(P/2).Un]/(P/2.Un) =1
dc: lim [P/(2n.Un)]/(P/2.Un) =1 cad : lim 1/(n.Un^2) =1
d ou lim n.Un^2 =1 et enfin lim rac(n).Un=1
cordialement | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: limite d'une suite définie par tan Sujet: Re: limite d'une suite définie par tan  Jeu 03 Jan 2019, 12:48 Jeu 03 Jan 2019, 12:48 | |
| je donne une solution conforme aux programmes de 2BSM
on considère la fct f définie par : f(o)=1 et f(x)=tan(x)/x .
on a lim (P/2)Un = 0 donc lim f[(P/2).Un]=f(0) car f est une continue en 0 et donc :
lim [tan(P/2).Un]/(P/2.Un) =1
dc: lim [P/(2n.Un)]/(P/2.Un) =1 cad : lim 1/(n.Un^2) =1
d ou lim n.Un^2 =1 et enfin lim rac(n).Un=1
cordialement | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: limite d'une suite définie par tan Sujet: Re: limite d'une suite définie par tan  | |
| |
|
  | |
| | limite d'une suite définie par tan |  |
|
