Limite d'une suite:

Soient 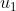et 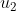deux réels strictement positifs.
Soient la suite définie par la données de ces deux premiers termes et par la relation de récurrence: .
Déterminez .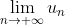
Bonne chance.

par récurrence immédiate u_n est strictement positive (ne s'annule pas),
on pose v_n=1/u_n,
on a donc v_(n+2)=1/2(v_(n+1)+v_n)
résolution d'équation de second degré et blabla donne :
v_n = a+b(-1/2)^n
où a = 2/3v_1+1/2v_2 et b=4/3(v_2-v_1)
et donc v_n converge vers a, par suite u_n converge vers 1/a

Mohammed_Lahlou a écrit:

par récurrence immédiate u_n est strictement positive (ne s'annule pas),
on pose v_n=1/u_n,
on a donc v_(n+2)=1/2(v_(n+1)+v_n)
résolution d'équation de second degré et blabla donne :
v_n = a+b(-1/2)^n
où a = 2/3v_1+1/2v_2 et b=4/3(v_2-v_1)
et donc v_n converge vers a, par suite u_n converge vers 1/a

Oui, l'idée est bonne mais il se peut qu'il y a des erreurs de calculs.
L'exercice est tiré d'une épreuve de l'ENSAM Meknes, où ils ont passé par les matrices et la diagonalisation pour déterminer la solution de la relation de récurrence d'ordre 2...

J'étais presque sûr pour la faute de calcul, au temps pour moi .
Bon ca va faire deux ans que j'essaye d'écrire en latex, en vain !
tu utilises codecogs.com/latex/eqneditor? si oui comment les insérer ici?

Mohammed_Lahlou a écrit:

par récurrence immédiate u_n est strictement positive (ne s'annule pas),
on pose v_n=1/u_n,
on a donc v_(n+2)=1/2(v_(n+1)+v_n)
résolution d'équation de second degré et blabla donne :
v_n = a+b(-1/2)^n
où a = 2/3v_1+1/2v_2 et b=4/3(v_2-v_1)
et donc v_n converge vers a, par suite u_n converge vers 1/a

v_(n+2)-v_(n+1)=-1/2(v_(n+1)-v_n)

==> la suite (v_(n+1)-v_n) est géométrique de raison -1/2
==>v_(n+1)-v_n=(-1/2)^n (v_1-v_0)

Par télescopage, v_n-v_0=2(1-(-1/2)^n )(v_1-v_0)/3
==> v_n--->v_0+2(v_1-v_0)/3=(2v_1+v_0)/3

Mohammed_Lahlou a écrit:

J'étais presque sûr pour la faute de calcul, au temps pour moi .
Bon ca va faire deux ans que j'essaye d'écrire en latex, en vain !
tu utilises codecogs.com/latex/eqneditor? si oui comment les insérer ici?

Tu cites mon message initial, et tu écris aux bonnes places. C'est d'ailleurs la méthode que j'utilise!

nmo a écrit:

Mohammed_Lahlou a écrit:

J'étais presque sûr pour la faute de calcul, au temps pour moi .
Bon ca va faire deux ans que j'essaye d'écrire en latex, en vain !
tu utilises codecogs.com/latex/eqneditor? si oui comment les insérer ici?

Tu cites mon message initial, et tu écris aux bonnes places. C'est d'ailleurs la méthode que j'utilise!

Merci bien ! je n'y est jamais pensé