exercice d'olympiade

salut!
voici un petit exercice d'olympiade de T.C.S : amusez vous à le faire!!
considérons un repère orthogonal et normé.
(C) est un cercle de centre B(2;2) et de rayon 2.
la droite (D) est une tangente au cercle (C) et qui passe par le point A(6;0).
détérmine le point d'intersection de la droite (D) avec l'axe des ordonnées.

2 systèmes (po d'amusmant )

c pour les T.C!!! c pourquoi!

Voici un nouveau exercice:
Répondez analytiquement (en choisissant un repère):
ABC est un triangle.
Soient I et J les milieux de AC et de BI.
La droite AJ coupe la droite BC en D.
1/Montrez que BD=BC/3.(vecteurs)
2/Ecrivez AJ en fonction de AD.(vecteurs)
Bonne chance.

Je réponds pour le premier exercice:
Après avoir dessiné une figure, on procède comme suit:
la droite (D) est une tangente au cercle (C) au point E(x,y).
En premier temps, on trouve les coordonnée du point E.
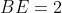
On a car E est un point du cercle.
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
D'autre part, on a le triangle ABE est rectangle en E.
Donc d'après pytagore, on a .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Pour trouver les coordonnéec, on résoud le système suivant: .
On procède par substition:
On a .
Donc .
Donc .
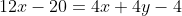
Donc .
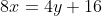
Donc .
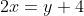
Donc .
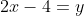
On remplace dans la première équation .
Donc .
Donc .
Donc .
On calcule le discriminent: .
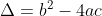
Donc .
Donc .
Donc .
Donc .
Comme le discriminent est positif, l'équation admet deux solutions distincts x1 et x2.
Et on a et .
Donc et .
Donc et .
Donc et .
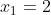
Donc et .
Si x=2, alors 2x-4=y.
Donc y=2*2-4.
Donc y=4-4.
Donc y=0.
Ainsi E(2,0).
Si x=18/5, alors 2x-4=y.
Donc y=2*18/5- 4.
Donc y=36/5- 20/5.
Donc y=16/5.
Ainsi E(18/5,16/5).
En un deuxième temps, on détérmine le point d'intersection de la droite (D) avec l'axe des ordonnées.
Le premier cas:
La droite (D) passe par E(2,0) et A(6,0).
Donc la droite (D) est l'axe des abcisses.
Donc la droite (D) coupe l'axe des ordonnées en O(0,0).
Le second cas:
La droite (D) passe par E(18/5,16/5) et A(6,0).
La droite (D) a pour équation cartésienne: .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
On note M(x,y) le point d'intersection de la droite (D) avec l'axe des ordonnée.
Pour déterminer les coordonnée de M, on résoud le système: .
Donc .
Donc .
Donc .
D'ou M(0,8 ).
J'espère que le résultat soit juste.
Sauf faute de calcul.

salam

exo1 : pour nmo

c'est troooooop looooooooooonnnnnnng

-----------------------------------supposons D coupe (Oy) en C

le cercle est tangent à (Ox) en(2,0) et à (Oy) en H(0,2)

T son point de contact avec D , on a CT=CH=x

OC² + OA² = AC² =====> (OH+HC)² +OA² = (AT+TC)²

(2+x)² + 6² = (4+x)²

====> x=6

====>C(0, 8 )


.