| | problème N°96 de la semaine (27/08/2007-02/09/2007) |  |
|
+21callo mni rockabdel huntersoul abdellatif Einshtein ali_tox robalro Yalcin taredot ali 20/20 saad007 selfrespect zikovitch9 Kendor radouane_BNE bouanou25 Infophile Weierstrass abdou20/20 samir 25 participants |
|
| Auteur | Message |
|---|
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 02:42 Lun 27 Aoû 2007, 02:42 | |
| | |
|
  | |
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 02:44 Lun 27 Aoû 2007, 02:44 | |
| salut
chaque participant doit poster sa solution ( format word ) par E-MAIL
amateursmaths@yahoo.fr
(Indiquer votre nom d'utilisateur dans la réponse envoyée )
puis il poste le message suivant ici "solution postée"
pour plus d'information voir les conditions de participation
Merci | |
|
  | |
abdou20/20
Expert sup

 Nombre de messages : 713 Nombre de messages : 713
Age : 33
Localisation : rabat
Date d'inscription : 12/06/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 09:31 Lun 27 Aoû 2007, 09:31 | |
| bonjour samir
solution postee
solution non trouver par l'administration | |
|
  | |
Weierstrass
Expert sup

 Nombre de messages : 2079 Nombre de messages : 2079
Age : 35
Localisation : Maroc
Date d'inscription : 03/02/2006
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 09:33 Lun 27 Aoû 2007, 09:33 | |
| postée
solution non trouver par l'administration | |
|
  | |
Infophile
champion de la semaine

 Nombre de messages : 15 Nombre de messages : 15
Age : 35
Date d'inscription : 02/06/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 11:17 Lun 27 Aoû 2007, 11:17 | |
| Bonjour, Solution postée. voici la solution d'infiphile | |
|
  | |
bouanou25
Débutant

Nombre de messages : 9
Date d'inscription : 04/08/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 11:21 Lun 27 Aoû 2007, 11:21 | |
| solution postee
solution non trouver par l'administration | |
|
  | |
Invité
Invité
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 12:56 Lun 27 Aoû 2007, 12:56 | |
| solution postéé  solution non trouver par l'administration solution non trouver par l'administration |
|
  | |
radouane_BNE
Modérateur

 Nombre de messages : 1488 Nombre de messages : 1488
Localisation : Montréal
Date d'inscription : 11/01/2006
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 13:28 Lun 27 Aoû 2007, 13:28 | |
| salut!
solution postée.
voici la solution de boukharfane
posons y=x+2005.
l'équation devient y(y+2)(y+4)(y+6)+16=0
<=>(y²+6y)(y²+6y+8 )+16=0
<=>(y²+6y)²+2*4*(y²+6y)+4²=0
<=>(y²+6y+4)²=0
d'où y=(-6+rac(20))/2 ou y=(-6-rac(20))/2. | |
|
  | |
Kendor
Féru
Nombre de messages : 64
Localisation : Malakoff (92240)
Date d'inscription : 13/12/2005
 |  Sujet: Solution au problème de la semaine n°96 par Kendor Sujet: Solution au problème de la semaine n°96 par Kendor  Lun 27 Aoû 2007, 13:43 Lun 27 Aoû 2007, 13:43 | |
| Salut à tous!
Solution postée.
voici la solution de kendor
Soit l’équation (E1)
(x+2005)(x+2007)(x+2009)(x+2011)+16=0
Soit y=x+2008
(E1) devient (E2)
(y-3)(y-1)(y+1)(y+3)+16=0
Donc (y²-9) (y²-1) +16=0
Donc y4-10y²+25=0
Donc (y²-5)²=0
Donc y²=5
Donc y=√5 ou y=-√5
Donc x=y-2008=√5-2008 ou x=-√5-2008
A+
Kendor | |
|
  | |
zikovitch9
Débutant
 Nombre de messages : 2 Nombre de messages : 2
Age : 34
Date d'inscription : 23/08/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 13:48 Lun 27 Aoû 2007, 13:48 | |
| Salut à tous
Solution postée .
solution non trouver par l'administration | |
|
  | |
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 13:58 Lun 27 Aoû 2007, 13:58 | |
| Salam, Solution posteé. voici la solution de selfrespectlequation equivaut :
(x+2005)(x+2011)(x+2007)(x+2009)=-16
==> (x²+4016x+4032055)((x²+4016x+4032055+ =-16 =-16
==>y(y+ =-16 (y=x²+4016x+4032055) =-16 (y=x²+4016x+4032055)
==> y=-4
==> x²+4016x+4032059=0 (D=20)
==> x={-2008+rac(5)} ou x={-2008-rac(5)}
reciproquemnt ces deux valeurs co,viennent .
S={-2008+rac(5) , -2008-rac(5} | |
|
  | |
saad007
Expert sup

 Nombre de messages : 923 Nombre de messages : 923
Age : 35
Localisation : espace noir
Date d'inscription : 10/02/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 14:07 Lun 27 Aoû 2007, 14:07 | |
| bonjour
solution postee
voici la solution de saad007
on a
(x+2005)(x+2011)=x²+4016x+4032055
et
(x+2007)(x+2009)=x²+4016x+4032063
= x²+4016x+4032055+8
posons :Y=x²+4016x+4032055
alors Y(Y+8 )=-16
donc la solution possible est Y=-4
alors x²+4016x+4032055= -4
x²+4016x+4032059=0
et enfin de compte
x={-2008+rac(5)} ou x={-2008-rac(5)}
reciproquemnt ces deux valeurs marche a merveille.
S={-2008+rac(5) , -2008-rac(5)}
merci
Dernière édition par le Lun 03 Sep 2007, 15:35, édité 2 fois | |
|
  | |
ali 20/20
Maître

 Nombre de messages : 239 Nombre de messages : 239
Date d'inscription : 01/07/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 15:33 Lun 27 Aoû 2007, 15:33 | |
| salut tt monde solution postée Voici la solution de ali20/20 alors pour l'equation on a
(2005+x)(2007+x)(2009+x)(2011+x)+16=0
donc on pose a=2007+x
alors on a
(a-2)(a+2)((a+2)-2)((a+2)+2)+6=0
donc
(a^2-4)((a+2)^2-4)+16=0
alors posons b=a+1=2008+x
((b-1)^2-4)((b+1)^2-4)+16=0
alors (b^2-1)^2-4[color=black](b^2+2)+32=0 donc b^4-2b^2+1-4([color:af49=black:af49]b^2+2)+32=0 b^4-6b^2+25=0 en utilisant delta on trouve que delta=36-100=-64<0 alors delta<0 donc l'ensemble de solution est vide wa salamo 3laykom wra7mato lah ce la ou je me suis trompé((b-1)^2-4)((b+1)^2-4)+16=0
ce pas (b^2-1)^2-4(b^2+2)+32=0mais cé (b^2-1)^2-4(2b^2+2)+32=0 alors b^4-10b^2+25=0 donc b=rac5 ou b=-rac5 donc x=-2008-rac5 ou x=rac5-2008malheuresement:(   
Dernière édition par le Lun 03 Sep 2007, 18:52, édité 1 fois | |
|
  | |
taredot
Débutant

 Nombre de messages : 5 Nombre de messages : 5
Age : 36
Date d'inscription : 04/07/2006
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 15:40 Lun 27 Aoû 2007, 15:40 | |
| solution postée
Voici la solution de taredhot
assalamou 3alaykoum wa ra7matou allah
on pose f(x)=(x+2005)*(x+2007)*(x+2009)*(x+2011)+16
et X=x+2005
on aura f(X)=X*(X+2)*(X+4)*(X+6)+16 cette fonction est toujours positive comme on va le montrer dc f(t)=0=>t est un extremum de f
vu qu'elle n'est constante sur aucun intervalle d'ou f(x)=0 => f '(x)=0 (la reciproque est fausse)
f est derivable sur R vu que c'est un polynome
=>f '(X)=4(X^3+9*X^2+22*X+12) on a f '(-3)=0 d'ou f '(X)=4*(X+3)*(X^2+6*X+4)=4*(X+3)*(x+((6+racine(20))/2))*(x-((-6+racine(20))/2))
les racines de f '(X) sont : -3 , 1/2*(-6-racine(20)) , 1/2(-6+racine(20))
on remplace dans f(X) et on aura en fin de compte S(X)={1/2*(-6-racine(20)) , 1/2*(-6+racine(20))}
et enfin S={1/2*(-6-racine(20))-2005 ; 1/2*(-6+racine(20))-2005)}
et merci | |
|
  | |
Yalcin
champion de la semaine
Nombre de messages : 21
Date d'inscription : 19/09/2005
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 15:53 Lun 27 Aoû 2007, 15:53 | |
| solution postée
voici la solution de yalcin
posons f(x)=(x+2005)(x+2007)(x+2009)(x+2011)+16
alors f(Y-(x+2005))=Y(Y+2)(Y+4)(Y+6)+16
et on obtient f((X-3)-(x+2005))=(X-3)(X-1)(X+1)(X+3)+16
d'où f((X-3)-(x+2005))=(X²-9)(X²-1)+16
ie f((X-3)-(x+2005))=X^4-10X+25
d'où f((X-3)-(x+2005))=(X²-5)²
d'où f(Y-(x+2005))=((Y+3)²-5)²
f(x)=((x+2005+3)²-5)²
f(x)=((x+2008)²-5)²
donc f(x)=0 donne (x+2008)²-5=0 , ie (x+2008)=+rac(5) ou x+2008=-rac(5)
d'où x=+rac(5)-2008 ou x=-rac(5)-2008 | |
|
  | |
robalro
Débutant
Nombre de messages : 6
Date d'inscription : 17/12/2005
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 19:46 Lun 27 Aoû 2007, 19:46 | |
| Bonjour ! Solution postée  voici la solution de robalro Voici ma solution. Par symétrie, je vais me baser sur le nombre 2008. voici la solution de robalro Voici ma solution. Par symétrie, je vais me baser sur le nombre 2008.
Notons A(x) = (x+2005)(x+2007)(x+2009)(x+2011) + 16
A(x) = (x+2008-3)(x+2007)(x+2009)(x+2011) + 16
A(x) = (x+2008)(x+2007)(x+2009)(x+2011) - 3.(x+2007)(x+2009)(x+2011) + 16
A(x) = (x+2008)(x+2007)(x+2009)(x+208+3) - 3.(x+2007)(x+2009)(x+2011) + 16
A(x) = (x+2008)²(x+2007)(x+2009) - 3.(x+2007)(x+2009)(x+2011)+3.(x+2008)(x+2007)(x+2009) + 16
A(x) = (x+2008)²(x+2007)(x+2009) - 9.(x+2007)(x+2009) + 16
A(x) = (x+2008)²(x+2008-1)(x+2009) - 9.(x+2007)(x+2009) + 16
A(x) = (x+2008)^3.(x+2009) - 9.(x+2007)(x+2009) - (x+2008)²(x+2009) + 16
A(x) = (x+2008)^3.(x+2008+1)-9.(x+2007)(x+2009)-(x+2008)²(x+2009) + 16
A(x) = (x+2008)^4 - 9.(x+2007)(x+2009) - (x+2008)²(x+2009) + (x+2008)²(x+2008) + 16
A(x) = (x+2008)^4 - 9.(x+2008-1)(x+2008+1) - (x+2008)² + 16
A(x) = (x+2008)^4 - 9.(x+2008)² - (x+2008)² + 16 + 9
A(x) = (x+2008)^4 - 10.(x+2008)² + 25
On cherche à résoudre A(x) = 0
Posons alors t = x + 2008 et X = t² . On obtient alors : X² - 10X +25 = 0 ie (X-5)² = 0
D'où X = 5 ainsi t1 = -rac(5) ou t2 = rac(5)
Donc x1 = -2008-rac(5) et x2 = -2008+rac(5)
Ainsi A(x) = (x+2008+rac(5))²(x+2008-rac(5))²
Conclusion : L'équation possède 2 solutions dans IR qui sont :
x1 = -2008-rac(5) et x2 = -2008+rac(5) | |
|
  | |
ali_tox
Maître

 Nombre de messages : 107 Nombre de messages : 107
Date d'inscription : 04/02/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Lun 27 Aoû 2007, 23:15 Lun 27 Aoû 2007, 23:15 | |
| solution postée
voici la Solution de ali_tox
On a l’équation E : (2005+x)(2007+x)(2009+x)(2011+x)+16=0
On admet que 2005+x=y
doncE y(y+2)(y+4)(y+6)+16=0
y^4+12y^3+44y^2+48y+16=0
(y²)²+2*6y²*y+36y²+8y²+48y+16=0
(y²+6y)²+2*4*(y²+6y)+4²=0
(y²+6y+4)²=0 donc y²+6y+4=0
Alors y= -3-racine5 ou y= -3+racine5
Donc x= -2008-racine5 ou x= racine5-2008 | |
|
  | |
Einshtein
Maître

 Nombre de messages : 205 Nombre de messages : 205
Age : 34
Date d'inscription : 06/03/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Mar 28 Aoû 2007, 00:52 Mar 28 Aoû 2007, 00:52 | |
| salut !
solution postée
voici la solution de Einshtein!
(x+2005)(x+2007)(x+2009)(x+2011)+16=0 (*)
on pose
L=x+2005
donc
(*) <=>L(L+2)(L+4)(L+6)+16=0
<=>L^4+12L^3+44L²+48L+16=0
<=>(L²+6L+4)²=0
=>L²+6L+4=0
delta=36-16=20
L1=(-6-rac(20))/2=-3-rac(5)
L2=(-6+rac(20))/2=-3+rac(5)
donc lequation(*) a deux solution:
x1=-2005-3-rac(5)=-2008-rac(5)
X2=-2005-3+rac(5)=-2008+rac(5)
S={(-2008-rac(5)),(-2008+rac(5))} | |
|
  | |
abdellatif
Féru

 Nombre de messages : 42 Nombre de messages : 42
Age : 35
Date d'inscription : 15/06/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Mar 28 Aoû 2007, 16:50 Mar 28 Aoû 2007, 16:50 | |
| salut tt le monde
solution postée
voici la solution d abdellatif
on pose a=x+2005
donc l equation equivale: a(a+2)(a+4)(a+6)+16=0
alors: (a²+6a)(a²+6a+8 )+16=0
Donc (a²+6a)²+8(a²+6a)+16=0
donc (a²+6a+4)²=0
Alors: a²+6a+4=0
donc a=-3-rac(5) ou bien a=-3+rac(5)
Alors les solution de cet equation sont:
x1=-2008-rac(5) et x2=-2008+rac(5)
wa ssalamo 3alaykom | |
|
  | |
huntersoul
Expert sup

 Nombre de messages : 1373 Nombre de messages : 1373
Age : 33
Localisation : In my mind
Date d'inscription : 19/02/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Mar 28 Aoû 2007, 22:25 Mar 28 Aoû 2007, 22:25 | |
| Solution postée voici la solution de huntersol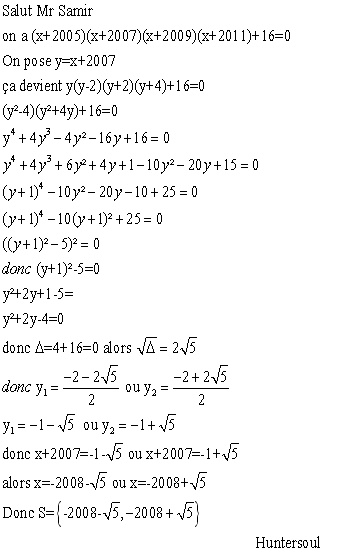 | |
|
  | |
rockabdel
Maître
Nombre de messages : 264
Date d'inscription : 15/09/2006
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Mer 29 Aoû 2007, 12:37 Mer 29 Aoû 2007, 12:37 | |
| postée
Voici la Solution de rockabdel
E1---(x+2005)(x+2007)(x+2009)(x+2011)+16=0
On pose x+2008=a
E1 ó (a-3)(a-1)(a+1)(a+3)+16=0
ó (a²-9)(a²-1)+16=0
ó a^4-10a+25=0
ó (a²-5)²=0
ó a=V5 ou a=-V5
ó x=V5-2008 ou x=-V5-2008 | |
|
  | |
mni
Maître

 Nombre de messages : 218 Nombre de messages : 218
Age : 33
Localisation : casa
Date d'inscription : 30/05/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Jeu 30 Aoû 2007, 16:44 Jeu 30 Aoû 2007, 16:44 | |
| slt tt le monde solution envoyé
voici la solution de mni
on pose X=x+2005
lequation A devient
A=X(X+2)(X+4)(X+6)+16=0
apres des suites de calculs on obtient
A=(X°2+4+6X)°2=0
donc cette equation a deux solution
X1=(-6+rac20)/2
X2=-(6+rac20)/2
c qui veut dire que
S=(-6+rac20)/2-2005 ET -(6+rac20)/2 -2005 | |
|
  | |
callo
Expert sup

 Nombre de messages : 1481 Nombre de messages : 1481
Age : 34
Localisation : paris
Date d'inscription : 03/03/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Jeu 30 Aoû 2007, 22:33 Jeu 30 Aoû 2007, 22:33 | |
| solution postée;)
voici la solution de callo
On pose : t=2005+x
L’equation nous donne :
t^4+12t^3+44t²+48t+16=0
soit :
f(x)= t^4+12t^3+44t²+48t+16
en calculant f’(x) on constate qu’elle ^peut facilement se factoriser par
4(x+3)
Ce qui nous donne :
F’(x)=4(x+3)(x+3+rac(5))(x+3-rac(5))
Et en dressant le tableau de variation :on constate que :
x<-3-rac(5) = f(x)>f(-3-rac(5))>0
-3-rac5<x<-3 = 0<f(-3-rac5)<f(x)
-3<x<-3+rac5 == f(x)>f(-3)>0
Et en remplaçant -3+rac5
On constate que f(x)>=f(-3+rac5)=0
d’où -3+rac5 est le seul a vérifier f(x)=0
donc t=-3+rac5
x=-2008+rac5
S={-2008+rac5}
a+ | |
|
  | |
ilham_maths
Maître

 Nombre de messages : 130 Nombre de messages : 130
Age : 34
Localisation : Casablanca.
Date d'inscription : 06/08/2007
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Sam 01 Sep 2007, 00:50 Sam 01 Sep 2007, 00:50 | |
| salut tt le monde.
solution postée.
voici la solution de ilham_maths
peut etre j'ai bien donné la bonne réponse dans mon 1er message(elle est mal rédigée).
voilà ma 2 eme réponse:
(x+2005)(x+2007)(x+2009)(x+2011)+16=0
(x+2005)(x+2005+2)(x+2005+4)(x+2005+6)+16=0
(x+2005)^4+12(x+2005)^3+44(x+2005)^2+48(x+2005)+16=0
on pose x+2005=t
ce qui donne t^4+12t^3+44t^2+48t+16=0
(t^2)^2+12t^3+(6t)^2+8t^2++48t+16=0
(t^2+6t)^2+8(t^2+6t)+16=0
on a deltat=64-64=0
donc t^2+6t=-8/2=-4
t^2+6t+4=0
delta=36-1=20
donc t1=(-6-racine caré de20)/2=-3-racine caré de5
et t2=-3+racine caré de 5.
alors x=-(3+racine5+2005)ou x=-3+racine5-2005.
donc S={-3+racine5-2005}.
| |
|
  | |
aissa
Modérateur
 Nombre de messages : 640 Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  Sam 01 Sep 2007, 19:31 Sam 01 Sep 2007, 19:31 | |
| bonsoir tout le monde
Solution postée
Voici la solution d’aissa
on pose : x+2005=y
puis : y² + 6y= z
l'équation : devient (z+4)²=0
alors z= -4
y=-3+V(5) ou y= -3 + V(5)
donc S={-2008+V(5) , -2008 - V(5)} | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007) Sujet: Re: problème N°96 de la semaine (27/08/2007-02/09/2007)  | |
| |
|
  | |
| | problème N°96 de la semaine (27/08/2007-02/09/2007) |  |
|
