| | facile mais difficile |  |
|
|
| Auteur | Message |
|---|
nietzsche
Habitué

 Nombre de messages : 24 Nombre de messages : 24
Age : 35
Date d'inscription : 19/10/2007
 |  Sujet: facile mais difficile Sujet: facile mais difficile  Mar 15 Jan 2008, 10:58 Mar 15 Jan 2008, 10:58 | |
| bjr, comme chque fois j'ai pour vous un exo tres facile mais au meme temps difficile personnellement je m'arrive tjrs à une contradiction alors je le pose ici pour que les autres puisse tester leurs competences l'enoncé est:pour n'importe quel n £ Z prouver que la fraction est ne peut pas etre simplifiée 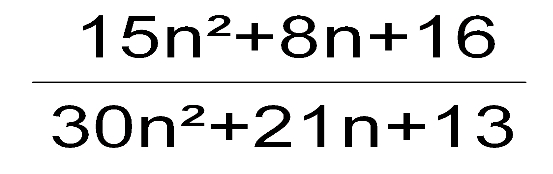 | |
|
  | |
o0aminbe0o
Expert sup
 Nombre de messages : 963 Nombre de messages : 963
Age : 34
Date d'inscription : 20/05/2007
 |  Sujet: Re: facile mais difficile Sujet: Re: facile mais difficile  Mar 15 Jan 2008, 13:08 Mar 15 Jan 2008, 13:08 | |
| prouver que PGCD(15n²+8n+16,30n²+21n+13)=1
posons PGCD(15n²+8n+16,30n²+21n+13)=d
donc d/15n²+8n+16 et d/30n²+21n+13 =>d/15n²+13n+3
d/15n²+13n+3 et d/15n²+8n+16 => d/5n-3
*d/5n-3 et d/15n²+8n+16 => d/(5n-3)(3n+3) et d/15n²+8n+16
=> d/2n+25
*d/5n-3 et d/15n²+13n+3 => d/(5n-3)(3n+4) et d/15n²+13n+3
=> d/2n+15
d/2n+15 et d/2n+25 => d/10
d/10 et d/30n²+21n+13 => d/n+3
=> d/2n+6
d/2n+15 et d/2n+6 => d/9
de ce fait d/10 et d/9 => d/1
donc PGCD(15n²+8n+16,30n²+21n+13)=1
ainsi la fraction proposée ne peut etre simplifiée
Dernière édition par le Mar 15 Jan 2008, 22:35, édité 1 fois | |
|
  | |
mni
Maître

 Nombre de messages : 218 Nombre de messages : 218
Age : 33
Localisation : casa
Date d'inscription : 30/05/2007
 |  Sujet: Re: facile mais difficile Sujet: Re: facile mais difficile  Mar 15 Jan 2008, 13:20 Mar 15 Jan 2008, 13:20 | |
| posant la fonction f define par
f(n)= (15n°2+8n +16)/(30n°2+21+13)
f(Df)=(0,41......0,77)
cest facile a demontrer
donc il nya aucun n £ Df qui realise f(n)£Z | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: facile mais difficile Sujet: Re: facile mais difficile  Mar 15 Jan 2008, 22:22 Mar 15 Jan 2008, 22:22 | |
| Salut,
Remarquer tout simplement que la parité du Numérateur est différente que celle du dénominateur ^^.
A+ | |
|
  | |
o0aminbe0o
Expert sup
 Nombre de messages : 963 Nombre de messages : 963
Age : 34
Date d'inscription : 20/05/2007
 |  Sujet: Re: facile mais difficile Sujet: Re: facile mais difficile  Mar 15 Jan 2008, 22:31 Mar 15 Jan 2008, 22:31 | |
| et qui te dit mr ALAOUI qu un nombre IMPAIR divise le numérateur et le dénominateur | |
|
  | |
o0aminbe0o
Expert sup
 Nombre de messages : 963 Nombre de messages : 963
Age : 34
Date d'inscription : 20/05/2007
 |  Sujet: Re: facile mais difficile Sujet: Re: facile mais difficile  Mar 15 Jan 2008, 22:34 Mar 15 Jan 2008, 22:34 | |
| - mni a écrit:
- posant la fonction f define par
f(n)= (15n°2+8n +16)/(30n°2+21+13)
f(Df)=(0,41......0,77)
cest facile a demontrer
donc il nya aucun n £ Df qui realise f(n)£Z on n a pas forcement 15n²+8n+16=k(30n²+21n+13) mais il faut aussi voir la deuxiemme possibilité 30n²+21n+13=k(15n²+21n+13) avec k£Q
Dernière édition par le Lun 28 Jan 2008, 19:20, édité 1 fois | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: facile mais difficile Sujet: Re: facile mais difficile  Mar 15 Jan 2008, 22:41 Mar 15 Jan 2008, 22:41 | |
| - o0aminbe0o a écrit:
- et qui te dit mr ALAOUI qu un nombre IMPAIR divise le numérateur et le dénominateur
Pardon j'ai pas compris? | |
|
  | |
o0aminbe0o
Expert sup
 Nombre de messages : 963 Nombre de messages : 963
Age : 34
Date d'inscription : 20/05/2007
 |  Sujet: Re: facile mais difficile Sujet: Re: facile mais difficile  Mar 15 Jan 2008, 22:43 Mar 15 Jan 2008, 22:43 | |
| 3/6 est une fraction qu on peut simplifié  | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: facile mais difficile Sujet: Re: facile mais difficile  Mar 15 Jan 2008, 22:50 Mar 15 Jan 2008, 22:50 | |
| Dit moi Amine est ce que PGCD(3,6)=1?? donc ton exemple n'existe jamais alors Faut ajouter une chose que je vais l'ajouter après.
reste a compléter ... | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: facile mais difficile Sujet: Re: facile mais difficile  | |
| |
|
  | |
| | facile mais difficile |  |
|
