|
| | Une droite dans le plan |  |
| | | Auteur | Message |
|---|
ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 |  Sujet: Une droite dans le plan Sujet: Une droite dans le plan  Dim 20 Jan 2008, 17:04 Dim 20 Jan 2008, 17:04 | |
| Bonjour les amis...
celui ci est un exercice du leçon "Une droite dans le plan" que je souhaite que nous participons à le résoudre .
ABC est un triangle . M est une point de (BC) et I le milieu de AM .
(CI) et (AB) sont deux droites sécantes dans D .
le droite qui passe de D et paralléle avec (AM) sécante (BC) dans N .
(AN) et (DM) sont deux droites sécantes dans J.
Prouve que B et I et J sont des points colinéaires. | |
|   | | mhdi
Expert sup
 Nombre de messages : 541 Nombre de messages : 541
Age : 32
Localisation : Tetouan
Date d'inscription : 21/11/2007
 |  Sujet: Re: Une droite dans le plan Sujet: Re: Une droite dans le plan  Dim 20 Jan 2008, 20:14 Dim 20 Jan 2008, 20:14 | |
| Que veut dire sécantes dans D? | |
|   | | ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 |  Sujet: Re: Une droite dans le plan Sujet: Re: Une droite dans le plan  Dim 20 Jan 2008, 20:19 Dim 20 Jan 2008, 20:19 | |
| - mhdi a écrit:
- Que veut dire sécantes dans D?
sécantes dans D = متقاطعان في D | |
|   | | mhdi
Expert sup
 Nombre de messages : 541 Nombre de messages : 541
Age : 32
Localisation : Tetouan
Date d'inscription : 21/11/2007
 |  Sujet: Re: Une droite dans le plan Sujet: Re: Une droite dans le plan  Dim 20 Jan 2008, 20:28 Dim 20 Jan 2008, 20:28 | |
| Je vais dessiner la figure. | |
|   | | ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 |  Sujet: Re: Une droite dans le plan Sujet: Re: Une droite dans le plan  Dim 20 Jan 2008, 20:32 Dim 20 Jan 2008, 20:32 | |
| - mhdi a écrit:
- Je vais dessiner la figure.
C'est trés bien  | |
|   | | ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 |  Sujet: Re: Une droite dans le plan Sujet: Re: Une droite dans le plan  Mar 22 Jan 2008, 12:22 Mar 22 Jan 2008, 12:22 | |
| | |
|   | | Invité
Invité
 |  Sujet: Re: Une droite dans le plan Sujet: Re: Une droite dans le plan  Mar 22 Jan 2008, 12:41 Mar 22 Jan 2008, 12:41 | |
| - ADISON a écrit:
- Ou est vous les amis ???
franchement on 'est pas arrivé à ce cours , mais je vé essayer pr toi  |
|   | | ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 | |   | | Invité
Invité
 |  Sujet: Re: Une droite dans le plan Sujet: Re: Une droite dans le plan  Mar 22 Jan 2008, 14:57 Mar 22 Jan 2008, 14:57 | |
| salut,  - Spoiler:
la figure: 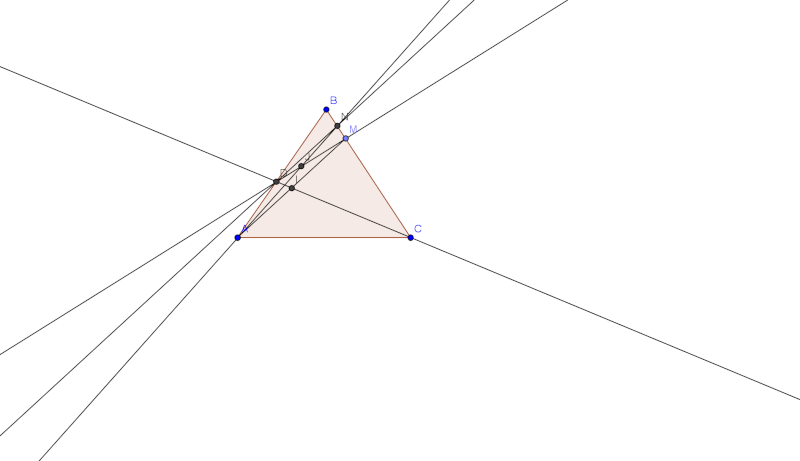 l'exo est vraiement classique , mais il ya bcp de calcul voilà: I) determinons les cordonnés de I dans le repère (A,vec(AC),vec(AB)):ona : M£[BC] , donc il existe un a de R+, tel que vec(BM)=a*vec(BC) ==> vec(BA)+vec(AM)=a*vec(BA)+a*vec(AC) ==> vec(AM)= a*vec(AC) +(1-a)*vec(AB) <=> M(a,1-a) - ona : I est le milieu de [AM] , et M(a,1-a), A(0,0) <=> I(a/2 , (1-a)/2) CQFD II) determinons les cordonnés de J dans le repère (A,vec(AC),vec(AB)):i) equation de la droite (CI): ona : (CI):y=ax+b et C(1,0) et I( a/2 , (1-a)/2 ) alors a= (1-a)/2 / (a-2)/2 = (1-a)/(a-2) en subsituant avec les cordonnés de C : b= (a-1)/(a-2) <=> (CI) : y= x* (1-a)/(a-2) + (a-1)/(a-2) CQFD ii) en déduire les cordonnés de D: ona : D£(AB) , donc : D(0,k) et puisque D£(CI): k= 0*(1-a)/(a-2) + (a-1)/(a-2) <=> k= (a-1)/(a-2) <=> D ( 0, (a-1)/(a-2)) CQFD iii) l'équation de delta : la droite passante par D et parallèle à (AM): soit delta : y= px+q - on va d'abord determiner l'équation de (AM) : puisque les cordonnés de A et M sont connus directement : (AM): y= (1-a)/a *x or (delta) // (AM) ==> p= (1-a)/a , par suite : delta : y= (1-a)/a *x + (a-1)/(2-a) CQFD iv) l'équation de (BC) : directement ona : (BC): y=-x+1 car les cordonnés de B et C sont connus.. v) en déduire les cordonnés de N: je te laisse le soin de résoudre le systeme  : { y= (1-a)/a *x + (1-a)/(2-a)}
{ y=-x+1 }soit alors (u,v) la solution du syteme <=> N(u,v) vi) l'équation de (AN) et (DM): puisque les cordonnés de A,N,D,M sont connus , alors il reste que faire des calculs pour trouver les équations de (AN) et (DM) aussi .. vii) en déduire les cordonnés de J: tu fais la meme chose que v) , mais cette fois ci avec les équation de (AN) et (DM).. III) en déduire le résultat:puisque B(0,1) et ona déja trouvé les cordonnés de I et J , il est facile alors de trouver les cordonnés de vec(BJ), et vec(JI) , et en calculant leur determinant , le résultat se découle facilement
|
|   | | ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 |  Sujet: Re: Une droite dans le plan Sujet: Re: Une droite dans le plan  Mer 23 Jan 2008, 12:44 Mer 23 Jan 2008, 12:44 | |
| - neutrino a écrit:
- salut,

- Spoiler:
la figure:  l'exo est vraiement classique , mais il ya bcp de calcul voilà: I) determinons les cordonnés de I dans le repère (A,vec(AC),vec(AB)):ona : M£[BC] , donc il existe un a de R+, tel que vec(BM)=a*vec(BC) ==> vec(BA)+vec(AM)=a*vec(BA)+a*vec(AC) ==> vec(AM)= a*vec(AC) +(1-a)*vec(AB) <=> M(a,1-a) - ona : I est le milieu de [AM] , et M(a,1-a), A(0,0) <=> I(a/2 , (1-a)/2) CQFD II) determinons les cordonnés de J dans le repère (A,vec(AC),vec(AB)):i) equation de la droite (CI): ona : (CI):y=ax+b et C(1,0) et I( a/2 , (1-a)/2 ) alors a= (1-a)/2 / (a-2)/2 = (1-a)/(a-2) en subsituant avec les cordonnés de C : b= (a-1)/(a-2) <=> (CI) : y= x* (1-a)/(a-2) + (a-1)/(a-2) CQFD ii) en déduire les cordonnés de D: ona : D£(AB) , donc : D(0,k) et puisque D£(CI): k= 0*(1-a)/(a-2) + (a-1)/(a-2) <=> k= (a-1)/(a-2) <=> D ( 0, (a-1)/(a-2)) CQFD iii) l'équation de delta : la droite passante par D et parallèle à (AM): soit delta : y= px+q - on va d'abord determiner l'équation de (AM) : puisque les cordonnés de A et M sont connus directement : (AM): y= (1-a)/a *x or (delta) // (AM) ==> p= (1-a)/a , par suite : delta : y= (1-a)/a *x + (a-1)/(2-a) CQFD iv) l'équation de (BC) : directement ona : (BC): y=-x+1 car les cordonnés de B et C sont connus.. v) en déduire les cordonnés de N: je te laisse le soin de résoudre le systeme  : { y= (1-a)/a *x + (1-a)/(2-a)}
{ y=-x+1 }soit alors (u,v) la solution du syteme <=> N(u,v) vi) l'équation de (AN) et (DM): puisque les cordonnés de A,N,D,M sont connus , alors il reste que faire des calculs pour trouver les équations de (AN) et (DM) aussi .. vii) en déduire les cordonnés de J: tu fais la meme chose que v) , mais cette fois ci avec les équation de (AN) et (DM).. III) en déduire le résultat:puisque B(0,1) et ona déja trouvé les cordonnés de I et J , il est facile alors de trouver les cordonnés de vec(BJ), et vec(JI) , et en calculant leur determinant , le résultat se découle facilement
Je te remercie énormément mon frére de m'avoir répondu en si peu de temps... | |
|   | | Invité
Invité
 |  Sujet: Re: Une droite dans le plan Sujet: Re: Une droite dans le plan  Mer 23 Jan 2008, 16:28 Mer 23 Jan 2008, 16:28 | |
| - ADISON a écrit:
- neutrino a écrit:
- salut,

- Spoiler:
la figure:  l'exo est vraiement classique , mais il ya bcp de calcul voilà: I) determinons les cordonnés de I dans le repère (A,vec(AC),vec(AB)):ona : M£[BC] , donc il existe un a de R+, tel que vec(BM)=a*vec(BC) ==> vec(BA)+vec(AM)=a*vec(BA)+a*vec(AC) ==> vec(AM)= a*vec(AC) +(1-a)*vec(AB) <=> M(a,1-a) - ona : I est le milieu de [AM] , et M(a,1-a), A(0,0) <=> I(a/2 , (1-a)/2) CQFD II) determinons les cordonnés de J dans le repère (A,vec(AC),vec(AB)):i) equation de la droite (CI): ona : (CI):y=ax+b et C(1,0) et I( a/2 , (1-a)/2 ) alors a= (1-a)/2 / (a-2)/2 = (1-a)/(a-2) en subsituant avec les cordonnés de C : b= (a-1)/(a-2) <=> (CI) : y= x* (1-a)/(a-2) + (a-1)/(a-2) CQFD ii) en déduire les cordonnés de D: ona : D£(AB) , donc : D(0,k) et puisque D£(CI): k= 0*(1-a)/(a-2) + (a-1)/(a-2) <=> k= (a-1)/(a-2) <=> D ( 0, (a-1)/(a-2)) CQFD iii) l'équation de delta : la droite passante par D et parallèle à (AM): soit delta : y= px+q - on va d'abord determiner l'équation de (AM) : puisque les cordonnés de A et M sont connus directement : (AM): y= (1-a)/a *x or (delta) // (AM) ==> p= (1-a)/a , par suite : delta : y= (1-a)/a *x + (a-1)/(2-a) CQFD iv) l'équation de (BC) : directement ona : (BC): y=-x+1 car les cordonnés de B et C sont connus.. v) en déduire les cordonnés de N: je te laisse le soin de résoudre le systeme  : { y= (1-a)/a *x + (1-a)/(2-a)}
{ y=-x+1 }soit alors (u,v) la solution du syteme <=> N(u,v) vi) l'équation de (AN) et (DM): puisque les cordonnés de A,N,D,M sont connus , alors il reste que faire des calculs pour trouver les équations de (AN) et (DM) aussi .. vii) en déduire les cordonnés de J: tu fais la meme chose que v) , mais cette fois ci avec les équation de (AN) et (DM).. III) en déduire le résultat:puisque B(0,1) et ona déja trouvé les cordonnés de I et J , il est facile alors de trouver les cordonnés de vec(BJ), et vec(JI) , et en calculant leur determinant , le résultat se découle facilement
Je te remercie énormément mon frére de m'avoir répondu en si peu de temps... de rien  , mais attention mon approche était plutot collègienne , car on n'apas vu ce cours , mais le étapes sont justes , alors je te conseille de refaire l'exo ( en suivant mes étapes si tu veux) , mais avec une méthode de tc , par ex: recalcule les équations des droites , mais avec une méthode que vs venez d'étudier   |
|   | | ADISON
Expert grade2
 Nombre de messages : 332 Nombre de messages : 332
Age : 32
Date d'inscription : 17/11/2007
 |  Sujet: Re: Une droite dans le plan Sujet: Re: Une droite dans le plan  Mer 23 Jan 2008, 20:23 Mer 23 Jan 2008, 20:23 | |
| - neutrino a écrit:
- ADISON a écrit:
- neutrino a écrit:
- salut,

- Spoiler:
la figure:  l'exo est vraiement classique , mais il ya bcp de calcul voilà: I) determinons les cordonnés de I dans le repère (A,vec(AC),vec(AB)):ona : M£[BC] , donc il existe un a de R+, tel que vec(BM)=a*vec(BC) ==> vec(BA)+vec(AM)=a*vec(BA)+a*vec(AC) ==> vec(AM)= a*vec(AC) +(1-a)*vec(AB) <=> M(a,1-a) - ona : I est le milieu de [AM] , et M(a,1-a), A(0,0) <=> I(a/2 , (1-a)/2) CQFD II) determinons les cordonnés de J dans le repère (A,vec(AC),vec(AB)):i) equation de la droite (CI): ona : (CI):y=ax+b et C(1,0) et I( a/2 , (1-a)/2 ) alors a= (1-a)/2 / (a-2)/2 = (1-a)/(a-2) en subsituant avec les cordonnés de C : b= (a-1)/(a-2) <=> (CI) : y= x* (1-a)/(a-2) + (a-1)/(a-2) CQFD ii) en déduire les cordonnés de D: ona : D£(AB) , donc : D(0,k) et puisque D£(CI): k= 0*(1-a)/(a-2) + (a-1)/(a-2) <=> k= (a-1)/(a-2) <=> D ( 0, (a-1)/(a-2)) CQFD iii) l'équation de delta : la droite passante par D et parallèle à (AM): soit delta : y= px+q - on va d'abord determiner l'équation de (AM) : puisque les cordonnés de A et M sont connus directement : (AM): y= (1-a)/a *x or (delta) // (AM) ==> p= (1-a)/a , par suite : delta : y= (1-a)/a *x + (a-1)/(2-a) CQFD iv) l'équation de (BC) : directement ona : (BC): y=-x+1 car les cordonnés de B et C sont connus.. v) en déduire les cordonnés de N: je te laisse le soin de résoudre le systeme  : { y= (1-a)/a *x + (1-a)/(2-a)}
{ y=-x+1 }soit alors (u,v) la solution du syteme <=> N(u,v) vi) l'équation de (AN) et (DM): puisque les cordonnés de A,N,D,M sont connus , alors il reste que faire des calculs pour trouver les équations de (AN) et (DM) aussi .. vii) en déduire les cordonnés de J: tu fais la meme chose que v) , mais cette fois ci avec les équation de (AN) et (DM).. III) en déduire le résultat:puisque B(0,1) et ona déja trouvé les cordonnés de I et J , il est facile alors de trouver les cordonnés de vec(BJ), et vec(JI) , et en calculant leur determinant , le résultat se découle facilement
Je te remercie énormément mon frére de m'avoir répondu en si peu de temps... de rien  , mais attention mon approche était plutot collègienne , car on n'apas vu ce cours , mais le étapes sont justes , alors je te conseille de refaire l'exo ( en suivant mes étapes si tu veux) , mais avec une méthode de tc , par ex: recalcule les équations des droites , mais avec une méthode que vs venez d'étudier , mais attention mon approche était plutot collègienne , car on n'apas vu ce cours , mais le étapes sont justes , alors je te conseille de refaire l'exo ( en suivant mes étapes si tu veux) , mais avec une méthode de tc , par ex: recalcule les équations des droites , mais avec une méthode que vs venez d'étudier   Pas de problémes mon frére.... Et je te remercie pour tes conseilles..  Et INCHALLAH je vais refaire l'exercice avec une méthode de TC... MERCI  | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Une droite dans le plan Sujet: Re: Une droite dans le plan  | |
| |
|   | | | | Une droite dans le plan |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
