inégalitée

soient a;b;c les longueurs des cotés d'un triangle , prouver que :

a^3+b^3+c^3+3abc-2b²a-2c²b-2a²c>=0

A+

utilise schur !ça peut aider mon petit(c'est dans le cours)

Alaoui.Omar a écrit:

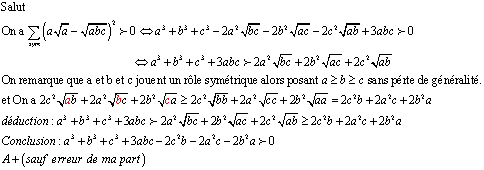lol es-tu sur que a,b,c jouent un role symetrique ?

Je l'ai écris donc c'est pas la peine de la réécrire n'est ce pas neutrino ? si tu as une autre proposition dit là pour la discuter!

Alaoui.Omar a écrit:

Je l'ai écris donc c'est pas la peine de la réécrire n'est ce pas neutrino ? si tu as une autre proposition dit là pour la discuter!

il ne jouent pas un role symetrique !!

par ex : f(a,c,b)=a^3+...3abc-2c²a-2b²c-2a²b#a^3+...3abc-2b²a-2c²b-2a²c

neutrino a écrit:

Alaoui.Omar a écrit:

Je l'ai écris donc c'est pas la peine de la réécrire n'est ce pas neutrino ? si tu as une autre proposition dit là pour la discuter!

il ne jouent pas un role symetrique !!

par ex : f(a,c,b)=a^3+...3abc-2c²a-2b²c-2a²b#a^3+...3abc-2b²a-2c²b-2a²c

suis les lignes et saute pas les étapes.

Alaoui.Omar a écrit:

neutrino a écrit:

Alaoui.Omar a écrit:

Je l'ai écris donc c'est pas la peine de la réécrire n'est ce pas neutrino ? si tu as une autre proposition dit là pour la discuter!

il ne jouent pas un role symetrique !!

par ex : f(a,c,b)=a^3+...3abc-2c²a-2b²c-2a²b#a^3+...3abc-2b²a-2c²b-2a²c

suis les lignes et saute pas les étapes.

tu as dis que puisque a,b,c jouent un role symetrique alors , on peut supposer que a>=b>=c , mais ici l'exppression n'est pas symetrique , alors ta démo est fausse

neutrino a écrit:

Alaoui.Omar a écrit:

neutrino a écrit:

Alaoui.Omar a écrit:

Je l'ai écris donc c'est pas la peine de la réécrire n'est ce pas neutrino ? si tu as une autre proposition dit là pour la discuter!

il ne jouent pas un role symetrique !!

par ex : f(a,c,b)=a^3+...3abc-2c²a-2b²c-2a²b#a^3+...3abc-2b²a-2c²b-2a²c

suis les lignes et saute pas les étapes.

tu as dis que puisque a,b,c jouent un role symetrique alors , on peut supposer que a>=b>=c , mais ici l'exppression n'est pas symetrique , alors ta démo est fausse

neutrino j pense qu'on peut suposer que a>b>c ms mm si le cas j pense qu'il ya une faute ds la démo de alaoui car ds ce cas on peut dire que ab>bb et bc>cc ms ac<aa

iverson_h3 a écrit:

neutrino a écrit:

Alaoui.Omar a écrit:

neutrino a écrit:

Alaoui.Omar a écrit:

Je l'ai écris donc c'est pas la peine de la réécrire n'est ce pas neutrino ? si tu as une autre proposition dit là pour la discuter!

il ne jouent pas un role symetrique !!

par ex : f(a,c,b)=a^3+...3abc-2c²a-2b²c-2a²b#a^3+...3abc-2b²a-2c²b-2a²c

suis les lignes et saute pas les étapes.

tu as dis que puisque a,b,c jouent un role symetrique alors , on peut supposer que a>=b>=c , mais ici l'exppression n'est pas symetrique , alors ta démo est fausse

neutrino j pense qu'on peut suposer que a>b>c ms mm si le cas j pense qu'il ya une faute ds la démo de alaoui car ds ce cas on peut dire que ab>bb et bc>cc ms ac<aa

nn on ne peut pas

essaie de suivre les étapes et remarque ou j'ai écris j'ai supposé ce que j'ai supposé .

ecoute omar , a,b,c ne jouent pas un role symetrique , et en plus tu as commis une faute comme a dit iverson_h3

Pour iverson consulte le cours des inégalité la page du réordonnement .neutrino aussi

Alaoui.Omar a écrit:

Pour iverson consulte le cours des inégalité la page du réordonnement .neutrino aussi

ah bon : , toi aussi fais la meme chose , pr apprendre quand , on pe ordonner les rééls

neutrino a écrit:

Alaoui.Omar a écrit:

Pour iverson consulte le cours des inégalité la page du réordonnement .neutrino aussi

ah bon : , toi aussi fais la meme chose , pr apprendre quand , on pe ordonner les rééls

j'ai croyais que je parle avec un individus conscient mais dommage comme Stof a dit tu es qu'un petit enfant inconscient .
wa dir chan lebrahech ytel3oulek fou9 rassek

lol , je suis étonné , mais li chaf chi 7aja y9oul layster

A+

Alaoui.Omar a écrit:

neutrino a écrit:

Alaoui.Omar a écrit:

Pour iverson consulte le cours des inégalité la page du réordonnement .neutrino aussi

ah bon : , toi aussi fais la meme chose , pr apprendre quand , on pe ordonner les rééls

j'ai croyais que je parle avec un individus conscient mais dommage comme Stof a dit tu es qu'un petit enfant manquer inconscience .
wa dir chan lebrahech ytel3oulek fou9 rassek

je crois que stof065 ta'infecté , à cet age tu te crois grand et sage lol , iwa hadahowa tbarhich wa illa fala

BSR à Vous Tous !!
Merci de ne pas vous quereller pour des broutilles !!!
Allez voir ICI ce qui m'est arrivé et vous allez vous régaler !!!
https://mathsmaroc.jeun.fr/premiere-f5/limite-exo-t7296-15.htm#58839
A+ et Amitiés à Vous Tous !
LHASSANE

neutrino a écrit:

Alaoui.Omar a écrit:

neutrino a écrit:

Alaoui.Omar a écrit:

Pour iverson consulte le cours des inégalité la page du réordonnement .neutrino aussi

ah bon : , toi aussi fais la meme chose , pr apprendre quand , on pe ordonner les rééls

j'ai croyais que je parle avec un individus conscient mais dommage comme Stof a dit tu es qu'un petit enfant manquer inconscience .
wa dir chan lebrahech ytel3oulek fou9 rassek

je crois que stof065 ta'infecté , à cet age tu te crois grand et sage lol , iwa hadahowa tbarhich wa illa fala

!!

salut tt le monde
je croix qu il faut arreter ce blabla inutil Neutrino a raison de dire que a,b et c ne jouent pas un rol symetrique ds cet expression mais ton raisonnement est peut etre correcte il suffit de dire qu on fait la mm chose si on suppose que b<a<c ou....au lieu de dire a,b et c jouent un rol symetrique !

Bonsoir,
quand j'ai parlé de la symétrie de a,bet c j'ai parlé de la symétrie dans cette exepression :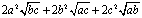
je défis tout le monde si il me dit quelle n'est pas symétrique.

alors cé qu il fallait dire et eviter ls blabla inutils car tt le monde a le droit de croire que tu parlais de l expression initiale!!

slt alaoui j l'ai consulter ms je pense que c ps comme sa qu'on l'applique sinon veillez ns expliquer votre passage ds ce qui est en rouge ds ta démo plz !!!!!!!
@+

reslt alaoui !!!!!!!!!
bé d'après ce que tu dis :
ab +bc+ac >= aa+bb+cc=a²+b²+c² ce qui est absolument faux
ou b1 g mal compris ce que vs avez fait si c le cas veillez m'eclairsir 1 peu
@+

wi cé vrai inverson-h3 le passage en question est a justifier malgré la symétrie de a,bet c dans l exepression indequée!

iverson_h3 a écrit:

reslt alaoui !!!!!!!!!
bé d'après ce que tu dis :
ab +bc+ac >= aa+bb+cc=a²+b²+c² ce qui est absolument faux
ou b1 g mal compris ce que vs avez fait si c le cas veillez m'eclairsir 1 peu
@+

là tu as raison iverson