la somme des diviseurs de n

autre question...
peut-on généraliser la deuxième question en trouvant des conditions sur a et b pour que l'equation 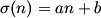ait des solutions.

n=P1^(a1)....Pn^(an) ( P1<...<Pn)

si n paire donc P1=2 et a1#0

donc n a des deviseur paire et impaire pour la somme des deviseur paire et tjrs paire
donc faut seulment discuter les deviseur impaire le nombre de deviseur impaire si (a2+1)..(an+1)
donc il faut que ce dernier soit impaire donc que soit (2<=i<=n) ai est paire ===> ai=2bi

donc n=2^a1*(P2^(2b2)....Pn^(2bn))=2^a1(P2^b2...Pn^(bn))^2=2^a1(A)²

la meme chose pour n est impaire

bien mohamed,mais c'est juste la partie facile de l'exercice...

oui,le premier est facile pour mais le dexieme(3nkchna mziaaaan) on a
sommes des diviseurs=S(n) est impaire,donc n=2^aq²
donc s(n)>=n+1+q+2q+2²q+...+2^aq+q²+2q²+2²q²+...+2^(a-1)q²
=n+1+q(2^(a+1)-1)+q²(2^a-1)>=n+1+2^aq+n/2>=3n/2
donc s(n)>=3n/2 et le reste est facile
mais j pense que l'equation est fausse
(sauf erreur)

des diviseurs de n sont 1,2,....,2^a,q,2q,....,2^aq,q^2,.....2^aq^2.
la somme =(1+q+q^2)(2^(a+1)-1)
l'equation devient 3((1+q+q^2)(2^(a+1)-1))=2^(a+2)q^2-17 ou
2^(a+1)(q^2+3q+3)=3(1+q+q^2)-17<3(1+q+q^2)
donc 2^(a+1)<3(1+q+q^2)/(q^2+3q+3)<3 et le reste se traite par la main.....
NB
sigma(n) est plutot la somme des diviseurs de n (et non sigma(n))
et n est positive comme a la premiere question.

c faux j pense car q n'est pas premier
n=π(p_i)^a_i donc S(n)=π((p_i)^a_i +(p_i)^(a_i-1)+...+1)=π((p_i)^(a_i+1)-1))/(p_i-1)

oui ,c vrai les egalités sont des inegalités , , j'ai juste donner une demarche pour la deuxieme .....

BJR à Toutes et Tous !!

J'ai retrouvé cet Exo sur le Forum " L'Ile des Maths " , intéressant à suivre ce Topic ; donc pas nécessaire
de vous pomper la soluce
( ce n'est pas dans ma nature ) MAIS je vous donne le Lien :

http://www.ilemaths.net/forum-sujet-216880.html

Bonne Fin de Dimanche acompagnée de Chergui chez Vous !!

LHASSANE

PS : @Selfrespect !! Sur ce même Lien , on demande de montrer que
SIGMA(n)<=n+nLn(n) et
C'EST PROUVE ( pour kalm !!! )
comme par ailleurs n+1<=SIGMA(n) alors tu as là une réponse à une question que tu as déjà posée sur le Forum
<< Donnez un équivalent simple de SIGMA(n) pour n assez grand >>

jolie question Kalm,c'est une essaie qui semble étre correcte mais ben qui sait....
pour la première question ma réponse était:
on peut mettre n sous sa forme en décomposition en facteurs premiers :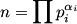

alors comme l'a déja signalé mahmoud, la somme des diviseurs de n est:
est bien c'est la clef de cet exo, il suffit alors de montrer que:
maintenant si on parvient à montrer que:

il suffit de sommer les deux cotés pour obtenir le résultat voulu.
je laisse ce job aux amateurs des inégalités,j'ai une réponse mais je veux pas bombarder tt à la fois...

la généralisation persiste encore,j'ésoere que quelqu'un peut nous donner une solution ou bien une indication,je suis trés interessé par cet exo:arrow:

boukharfane radouane a écrit:

jolie question Kalm,c'est une essaie qui semble étre correcte mais ben qui sait....
pour la première question ma réponse était:
on peut mettre n sous sa forme en décomposition en facteurs premiers :

alors comme l'a déja signalé mahmoud, la somme des diviseurs de n est:
est bien c'est la clef de cet exo, il suffit alors de montrer que:
maintenant si on parvient à montrer que:

il suffit de sommer les deux cotés pour obtenir le résultat voulu.
je laisse ce job aux amateurs des inégalités,j'ai une réponse mais je veux pas bombarder tt à la fois...

si on a sommé on va pas avoir le resultat,et aussi le produit