inégalité

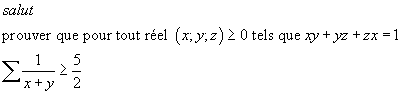(svp si quelqu un peut donner une solution avec cette substitution
a=x+y+z ; b=xy+yz+zx et c=xyz) merci d avance

h-o-u-s-s-a-m a écrit:

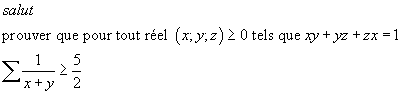
(svp si quelqu un peut donner une solution avec cette substitution
a=x+y+z ; b=xy+yz+zx et c=xyz) merci d avance

On met a+b+c=p,ab+ac+bc=q,abc=r;

L'inégalité est équivalente à:

(p²+q)/(p-r) >= 5/2

ou aussi:

2p²-5p+5r+2 >= 0,

Cas 1:

si p >= 2,

l'inégalité est équivalente à:

(p-2)(p-1/2)+5r/2 >= 0 ce qui est vrai,

Cas 2:

si p =< 2,

selon l'inégalité de Schur on a :

r >=(4p-p^3)/9,

en remlaçant dans la première inégalité on doit prouver que:

-5p^3-25p+18p²+18 >= 0,

=>-(p-2)(5p^2-8p+9) >= 0,

ce qui est vrai puisce que p-2 =< 0 et 5p²-8p+9 > 0.

salut

2p²-5p+5r+2 >= 0 , delta = 9-40r

pour que 2p²-5p+5r+2 >= 0 , delta < 0 => r >9/40

salut
merci les amis
juste une petite question est ce que cette substitution est efficace sur la majorité des inégalité a nombre de variable déterminé ou ça depond de l inégalité?

j pense qu elle est efficace pour les inegalités de trois variables

voiçi des resultats de
memath

merci yassine

a vrai dire ce n'est pas a memath amicalement.
le voila en français
https://mathsmaroc.jeun.fr/theoremes-et-formules-f26/technique-de-resolution-d-inegalites-a-3-variables-t4513.htm
c pour un autre .

merci a vous aussi greatesmaths