Préparation TSM:: L-1/Limites et continuité:p/Exercices.

Solution pour 65:

on pose P(x;y) : f(x+y) = f(x) + f(y)

1) P(0;0) : f(0) = f(0) + f(0) ===> f(0)=0

2) P(x;-x) : f(0) = f(x) + f(-x) ==> f(-x) = -f(x) ===> f est impair


3) f(nx) = f(x + x + ... +x) = f(x) + f(x) + ....+ f(x) = nf(x)
Alors d'apres 3)
on a x=1 => pour tout n£ IN : f(n) = nf(1) = an (a=f(1) £ IR)
et puisque f est impair donc f(-n) = - f(n) = -an = a(-n)
donc pour tout k£ Z f(k) = ak

soit d'abord (p;q)£ZxIN* tel que r= p/q £ Q alors:

f(q r) = qf(r) = f(p) = p f(1) =ap (car p£IN)

alors qf(r) = ap => f(r) = a (p/q) = ar

alors pour tout x£Q on a f(x) = ax

d'abord en utilisant la densité de Q dans IR :

Si f est supposée continue.Soit x un réel et (x_n)_n une suite de rationnels qui converge vers x.
On a donc :
(x_n)£Q ==> f(x_n) = a x_n passons à la limite en prenant le fait où f est continue sur IR donc:

lim(n->+00)f(x_n) = f(lim(n->+00) x_n) = a lim(n-->+00) x_n
=> f(x) = ax pour tout x£IR et a=f(1) £ IR ...
Alors calculons a:
f(2009)=2009a=2009^2008 =>a=2009^2007
Donc pour tout x£IR f(x)=x.(2009^2007)

Solution pour 66:
pour tout a£IR on a:lim(x->a)f(x)=lim(h->0)f(h+a) (En posant h=x-a)
Donc lim(x->a)f(x)=(lim(h->0) f(h))+f(a).
donc si f est continue en 0 on aura:
lim(x->a)f(x)=f(0)+f(a)
Et on a f(0) = f(0) + f(0) ===> f(0)=0
Alors lim(x->a)f(x)=f(a)

Donc si f est continue en 0;alors elle est continue sur R

Alors continuons avec ces 3 exercices:
Exercice 70:
f:[a;b]->[a;b] est une fonction continue sur [a;b]
Prouver que f admet un point fixe.
Exercice 71:
Soit f une fonction numérique continue sur R tq;
pour tt x£IR: f(x)=/= x
Prouver que fof(x)=x n'admet pas de solution dans R.
Exercice 72:
Soit f une fonction numérique continue sur [a;b] tq; f(0)=f(1)
Prouver q'il existe un nombre c de ]0;1[ tq:f(c)=(1-c)/(1+c)

Exercice 71 :

On f(x) une fonction continue sur IR , donc Lim f(x) quand x tend vers x0 = f(x0)
on a pour tout x de IR , f(x0) =/= x0 , donc Lim f(x) quand x tend vers x0 =/= x0 .(1)

On sait que si f(x) et g(x) sont continue sur un point ou domaine, alors gof ( ou fog) l'est aussi, donc fof(x) est continue sur IR .
et selon le théorème de limite on a Lim fof(x) quand x tend vers x0 =/= x0
puisque fof(x) est continue sur IR, alors fof(x) =/= x , quelque soit x de IR .

Solution pour 70:
a est un point fixe de f <=> f(a)=a
Donc soit c la solution de f(x)-x=0
Notons g(x)=f(x)-x . g est aussi continue sur [a;b]
On a 0 =< g(a)=<b-a et a-b =< g(b)=<0
alors puisque g est continue sur [a;b] ;g(b)=<0 et 0 =< g(a)
Et en utilisant le TVI g(x)=0 admet au moins une solution dans [a;b]
CQFD

Mim a écrit:

Exercice 71 :

On f(x) une fonction continue sur IR , donc Lim f(x) quand x tend vers x0 = f(x0)
on a pour tout x de IR , f(x0) =/= x0 , donc Lim f(x) quand x tend vers x0 =/= x0 .(1)

On sait que si f(x) et g(x) sont continue sur un point ou domaine, alors gof ( ou fog) l'est aussi, donc fof(x) est continue sur IR .
et selon le théorème de limite on a Lim fof(x) quand x tend vers x0 =/= x0
puisque fof(x) est continue sur IR, alors fof(x) =/= x , quelque soit x de IR .

Solution fausse veuillez rectifier.

Solution pour 71:
Raisonnons par l'absurde:
Supposons que fof(x)=x admet une solution "a" sur R

Et posons H(x)=f(x)-x donc H est est continue sur R et H(x)=0 n'admet aucune solution selon l'énoncé

Donc H(a)=f(a)-a et H(f(a))=f(f(a))-f(a)=a-f(a)
alors H(a).H(f(a))=-(f(a)-a)^2 <0
Donc selon le "TVI" H(x)= 0 admet une solution dans l 'intervalle de bornes f(a) et a .
D'où la contradiction.

pour 65 je dois encore lire le théorème qui parle de la densité de Q sur IR je n'ai jamais fait d'exercices pareils , pour les autres exercices , leurs solutions sont justes .

Je pense qu'il y a une faute ou une donnée manquante dans l'exercice 72

f(x)=-1 est continue et f(0)=f(1) mais l'équation f(x)=(1-x)/(1+x) n'admet aucune solution dans l'intervalle ]0;1[.

Oui tu as raison car vraiment j'ai essayé plusieurs méthodes avec cet exercice mais j'ai rien trouvé .

Alors je vous propose l'exercice suivant:
Exercice 73:
Soit f une fonction continue sur [a;b] tq: f(a)=f(b)
Prouver que l'équation f(x)=f(x+(b-a)/2) admet au moins une solution appartenante à l'intervalle [a;b]

Solution pour 73:
On pose
H(x)=f(x)-f(x+(b-a)/2) donc H est continue sur [a;b]==> H est continue sur [a;(a+b)/2]
ALORS
H(a)=f(a)-f((a+b)/2) et H((a+b)/2)=f((a+b)/2)-f(b)=f((a+b)/2)-f(a)
Donc :
H(a).H((a+b)/2)=-(f((a+b)/2)-f(a))^2=< 0
Donc d’après TVI H(x)=0 admet une solution appartenante à l'intervalle [a;b]
CQFD

Les exercices (De 74 à 84) sont faciles à faire se sont des applications direct du TVI.
Exercices 85:

Soient f et g deux fonctions continues sur R.
Et soient u et v deux fonctions de R vers R*+ tq u et v sont continues sur R et vérifiant:

A----(il existe (a,b) £IR^2); a<b et f(a)=u(a) et g(b)=v(b).
B----(pr tt x£IR-{a}) f(x) <u(x)
C----(pr tt x£IR-{b}) v(x) <g(x)
Prouver qu'il existe C de [a;b] tq:
f(c).g(c)=u(c).v(c)

Solution pour 85:
On pose H(x)=f(x).g(x)-u(x).v(x) alors H est continue sur R.
1-H(a)=f(a).g(a)-u(a).v(a)=u(a).(g(a)-v(a))
Et puisque -(pr tt x£IR-{b}) v(x) <g(x) et u(x)> 0 ===> H(a)>0

2-H(b)=f(b).g(b)-u(b).v(b)=v(b).(f(b)-u(a))
Et puisque (pr tt x£IR-{a}) f(x) <u(x) et v(x)> 0 ===> H(b)<0

Donc H(a).H(b)<0
Et selon le TVI l'équation H(x)=0 admet au moins une solution de [a;b]
CQFD

Exercice 86 :

f et g et u sont des fonctions numériques continues sur [a,b] tel que ,

quelque soit x de [a,b] , f(x) =< g(x)

soit h la fonction numérique définie sur [a,b] tel que ,
quelque soit y de [0,1] , h(x) = yf(x) + (1-y)g(x)

soit les ensembles A={x £ [a,b] : f(x) = u(x) } , B={x£ [a,b] : g(x) = u(x) } , C={x £ [a,b]:h(x)=u(x)} , prouvez que ( A=/= 0 et B=/= 0) => C=/= 0 .

Solution pour 86:

On pose P(x)=H(x)-u(x)=yf(x)+(1-y)g(x)-u(x)
Donc P(x) est continue sur [a;b]

Et puisque A=/=Ø donc il existe c de[a;b] tel que f(c)=u(c)
Alors P(c)=H(c)-u(c)=yf(c)+(1-y)g(c)-u(c)=(y-1)f(c)+(1-y)g(c)= (1-y)(g(c)-f(c))>=0
Et puisque B=/=Ø donc il existe T de[a;b] tel que g(T)=u(T)
Alors P(T)=H(T)-u(T)=yf(T)+(1-y)g(T)-u(T)=y(f(T)-g(T))=<0
Donc P(c).p(T)=<0 et d'après TVI on aura c=/=Ø

Si vous êtes intéressés, je peux partager avec vous des exercices tirés d'une série.

oui avec plaisir.

Exercice 1:

Etudier la continuité de la fonction f définie sur l'intervalle ]0,1] tel que:




tel que p/q est la forme réduite du rationnel x.


Exercice 2:

Montrer que la fonction f tel que:




n'admet pas de limite dans aucun point de .

Exercice 3:

Etudier la continuité de la fonction définie de IR-{-1} vers IR tel que:

.

Exercice 4:

Considérons la fonction f définie sur ]a,b[ tel que:

Montrer que f est bijective de ]a,b[ vers IR, et déterminer .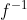

Exercice 5:

Soit f une fonction continue et positive sur IR+ tel que: .

Montrer que l'équation f(x)=x admet au moins une solution dans IR+.

Exercice 6:

Soit f une fonction continue sur [a,b] et x_1, x_2, .... , x_n et n des éléments de [a,b].

Montrer qu'il existe un réel c de [a,b] tel que: .

ali-mes tu peux donner une source de la série stp ?

Pour l'exercice 6 f doit être continue sur [a,b].

Othmaann a écrit:

ali-mes tu peux donner une source de la série stp ?

Comme j'ai déjà mentionné, les exercices viennent d'une série, et d'après le nom, c'est un professeur à moon lycée.

Othmaann a écrit:

ali-mes tu peux donner une source de la série stp ?

Effectivement, je vais éditer !

Les 2premiers exercices sont un bon entrainement pour une personne qui va dans quelques semaines être en MPSI et ayant déjà quelques notions comme la densité ...

Solution pour 4:
f est continue et dérivable sur ]a,b[
et f'(x)=1/(a-x)^2 + 1/(b-x)^2>0
Alors puisque f est continue et strictement croissante ===> f est bijective de ]a;b[ vers f(]a;b[) tel que f(]a;b[) =]-∞;+∞[ donc f est bijective de ]a,b[ vers IR.
Déterminons donc f^(-1)
On sait tout d'abord que f admet une fonction réciproque définie de IR vers ]a,b[ .
x=f(y)<==> x=1/(a-y) + 1/(b-y)
<==> xy^2+[2-x(a+b)]y+abx-a-b=0
Pour x=0 ==> f^(-1)(0)=(1/2).(a+b)
Pour x=/=0 on a :

Donc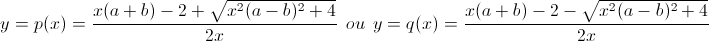

puisque f^(-1) est continue sur IR alors elle est continue en 0:

lim(x-->0) f^(-1)(x)=(1/2).(a+b)
Et puisque lim(x-->0)p(x)=(1/2).(a+b) et lim(x-->0) q(x)=/=(1/2).(a+b)
On aura: