exo de OMM 2005

On considère un entier naturel non nul et l'ensemble:
Déterminer pour que tous les éléments de 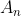soient des termes consécutifs dans une suite arithmétique.

Soit un tel entier naturel, et soit le plus petit nombre premier ne divisant pas , supposons alors que vérifie la propriété de l'énoncé dont la suite de ses éléments sera notée , si alors tout entier strictement compris entre et possède au moins un diviseur premier qui lui est inférieur ou égale donc aussi à mais strictement, donc par minimalité de , ce diviseur premier doit nécessairement diviser et par conséquent cet entier est bien exclus de , les entiers et apparaissent évidemment dans et y sont consécutifs d'après ce qui précède, la suite est du coup de raison , soit un entier premier avec et tel que qui existe à fortiori pusique (car , et par conséquent il est inversible on peut trouver donc un entier vérifiant , l'entier n'est pas premier puisqu'on a évidemment et il possède donc un diviseur premier et donc et par minimalité de on déduit que , Or c'est bien entendu une contradiction puisque , on déduit enfin que le cas traduit le fait que est premier avec tous les entiers impairs qui lui sont inférieurs et donc il est clairement une puissance de qui vérifie aisément la condition, le cas traduit exactement le fait que est premier puisqu'on aura