Une inégalité difficile à montrer ! Mais joli ^^

Soit (x,y,z) des réels strictement positives tel que x > y . Montrez que:



_{Crée par moi.}

M.Marjani a écrit:

Soit (x,y,z) des réels positive non nulls tel que x > y. Montrez que:

En effet, Difficile de démontrer quelque chose de faux. Contre-exemple : x=2, y=1, z=1, qui donne (LaTeX est revenu, youpiiiii ), qui est clairement négative.

oussama1305 a écrit:

M.Marjani a écrit:

Soit (x,y,z) des réels positive non nulls tel que x > y. Montrez que:

En effet, Difficile de démontrer quelque chose de faux. Contre-exemple : x=2, y=1, z=1, qui donne 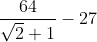(LaTeX est revenu, youpiiiii ), qui est clairement négative.

Certes

Edit:

La solution de nmo: https://mathsmaroc.jeun.fr/seconde-tronc-commun-f6/exercices-d-olympiade-t14310-930.htm

Un grand bravo à lui !

Ma solution proposé:

Avant, je voullais vous partager les lemmes crées par moi:

Lemme 1: (M.Marjani)

Soit (x,y) des réels positives tel que x>=y. On a V(x-y) >= V(x) - V(y) (1)

Démo:

Spoiler:

Lemme 2: (M.Marjani)

Soit (x,y) des réels positives. On a V(x) + V(y) >= V(x+y) (2)

Démo:

Spoiler:

Lemme 3: (M.Marjani)

Soit (x,y) des réls positives tel que x>=y. On a V(x+y)-V(x-y) =< 2V(y)

( Un résultat de (1) et (2) On peut la démontrer façilement)

La démonstration:

IAG ==> (x+y+z)^3 >= 27 xyz (N'était qu'un truc :p)

Donc il suffit de montré que:

Du premier coup, il fallait remarqué que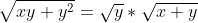

Par lemme (1) et (2) on déduit que: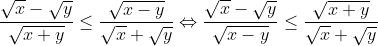

Et donc il suffit de prouver que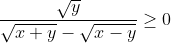

Qui est juste car V(y) >= 0 et V(x+y) > V(x-y) puisque x>y.

CQFD ^^

_{A la prochaine avec autre inégalité crée par moi :p}

salam ,

Pour les lemmes : tu peux débarrasser de 2 lemmes et montrer juste la deuxième ,

car les autres ne sont que des cas particuliers :

on a : Vx+Vy >= V(x+y) ==> prendre x = x-y et y=y ( pour ta premiere lemme )

Et prendre x=x-y et y= 4y == > V(x-y) + 2Vy >= V(x+3y) >= V(x+y) ..........

{}{}=l'infini a écrit:

salam ,

Pour les lemmes : tu peux débarrasser de 2 lemmes et montrer juste la deuxième ,

car les autres ne sont que des cas particuliers :

on a : Vx+Vy >= V(x+y) ==> prendre x = x-y et y=y ( pour ta premiere lemme )

Et prendre x=x-y et y= 4y == > V(x-y) + 2Vy >= V(x+3y) >= V(x+y) ..........

Joli démonstrations. Voiçi une autre plus fort, pour trois réels positives:

Lemme: (M.Marjani)

Soit (x,y) des réels positives tel que x>=m et y>=m. On a V(x-m)-V(y-m) =< V(x)-V(y)+V(m)
Démo:

Spoiler: