L'olympiade de Settat: (deuxième étape)

Exercice1:
a et b sont deux réels strictement positifs.
On considère le nombre X tel que: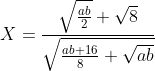
.
Calculez la valeur de X en montrant qu'il n'a pas de relation avec a et b.
Exercice2:
Trouvez tout les entiers naturels m et p pour que le nombre suivant appartient à l'ensemble des nombres rationels.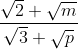
.
Exercice3:
Résolvez en IR^2 le système suivant:
.
Exercice4:
On considère un trapèze ABCD tel que (AB) et (CD) sont parallèle et AB=84 et CD=25.
On suppose que ce trapèze entoure un cercle.
Quel est le périmètre de ce trapèze.

J'ai réussi à résoudre le premier et le quatrième.
Quelle déception.!!
J'attends vos solutions impatiemment.
A vos stylos.

Citation :

On suppose que ce trapèze entoure un cercle.

Que veut-on dire par cela ? Merci d'être plus précis.

Dijkschneier a écrit:

Citation :

On suppose que ce trapèze entoure un cercle.

Que veut-on dire par cela ? Merci d'être plus précis.

Cela veut dire que les cotés du trapèzes tangentent le cercle.
Ou d'une autre manière le cercle est inscrit dans le trapèze.

Je présente mes solutions.
Exercice 1 :

Dijkschneier a écrit:

Je présente mes solutions.
Exercice 1 :

Effectivement, c'est ça ce que j'ai fait.

slt nmo voila ce que j'ai trouve pour exo 4:
puisque on un cercle C inscrit dans ce trapez alors comme t'a dis les cotes du trapezes tengentes le cercle dans les points x et y et z et g
alors on deduit que : ax=ay et bg=bx et dz=dy
alors la somme de ab+bc+ad+cd = ab+ cd +bg+gc+ay+dy= ab+cd+bx+ax+dz+cz=ab+cd+ab+cd (car bx+ax=ab et dz+cz=cd)
donc on aurait que ab+bc+as+cd=2ab+2cd=218
A+

pour le premier je viens de trouver la meme soluc que vous avez posez .....

Exercice 4 :

Soit a et b les longueurs respectifs des bases du trapèze.
Soit p le demi-périmètre du trapèze, et S sa surface.
Soit r le rayon du cercle inscrit.
Il est facile de prouver que 2r est la longueur de la hauteur du trapèze.
D'après les formules d'aires, on a :

D'où :
Le périmètre du trapèze est donc :

oui bonne soluc tu peux terminer ta demonstration avec :
2(a+b)=2a+2b=218

Slt nmo ,

pr le premier :

X²=(16+ab+8Vab)/(16+ab+8Vab)
Donc : X²=8/2=4

En déduit donc que : X=2

On peut écrire X sans relation avec a et b , donc X n'as pas de ralaltion évidement avec X.

Pr le deuxiéme j'ai tester , mais chui pas sure :

Posons : m=0 et p=0

Donc : (V2+Vm)/(V3+Vp)=(V2)/(V3)

Ce qui montre que (0.0) Pas une solution

Posons : m=2 et p=3

Donc : (V2+Vm)/(V3+Vp)=(V2+V2)/(V3+V3)=(V2)/(V3)
Ce qui montre que (m=2,p=3) Pas une solution

Posons m=8 et p = 12

Donc : (V2+Vm)/(V3+Vp)=(V2+V8)/(V3+V12)=(V2)/(V3)

On déduit donc que : tous les entiers naturels tels :

m=2*k² (k nombre naturel)
et p=3*k'² (k' nombre naturel)

ne sont pas des solutions .

Donc S=/ -{m=2*k²,p=3*k'²)

Posons m=3;p=2

(V2+Vm)/(V3+Vp)=(V2+V3)/(V3+V2)=1

Ce qui montre que (m=3;p=2) est une solution

Donc S={m=3;p=2}

le 3 EX , je le fais mtn , le 4éme aussi ))

pr le quatriéme :

S=(1/2)*p*r
S=(a+b)*r

Donc : (1/2)*p*r=(a+b)*r
(1/2)*p=(a+b)

Donc : p=2(a+b)
P=109*2 = 218

pr le 3éme je vois que B²+A²=2 , vous pensez que cà va nous aider ?
Donc : B=1 ou A=1 ou B=-1 ou A=-1
entrain de le faire.

slt j'ai pas pu encore resoudre le 3eme

Ta solution M.Marjani pour le troisième est fausse.
Essaye autrement.

Pour le quatrième, il existe une autre méthode que je vais poster plus tard.
Ou bien visitez la page suivante et en-bas de la page cliquez sur solution des olympiades de la première: http://mathall.eu.ma/

M.Marjani a écrit:

pr le 3éme je vois que B²+A²=2 , vous pensez que cà va nous aider ?
Donc : B=1 ou A=1 ou B=-1 ou A=-1
entrain de le faire.

C'est faux car il se peut que A=V2 et B=0.
Donc il faut chercher une autre relation entre A et B.

nmo a écrit:

Ta solution M.Marjani pour le troisième est fausse.
Essaye autrement.

Oui , mais ce sont pas les solutions finale. Je test les solutions de cette équation qui à deux inconues.

Je vais réflichir autre fois , aprés faire un EX.

Où êtes-vous pour le troisième. S'il vous plait je le veux dans un cour délai. Je n'ai pas pu le résoudre. Merci

Pour le 2 c'est m=3 et p=2
Posons :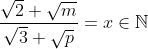

Donc :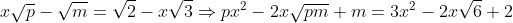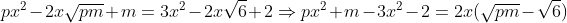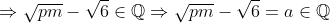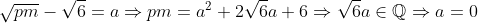



Donc :
pm=6
avec une disjonction de cas sur IN on trouve finalement p=2 et m=3
..
Sauf erreur ..

Il fallait résoudre le troisième, car il est important.
Et je ne sais pas comment prcéder.
Allez-y les matheux.

Exercice 3 :
On peut facilement prouver que 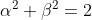. Appelons ce résultat : (1).
La première équation du système est 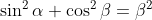, et équivaut à .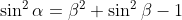
Il est connu que 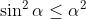, d'où 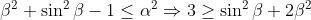, en utilisant (1). Appelons ce résultat : (2).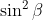
étant strictement positif, il vient que .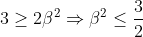
Et puisque (1), il vient que .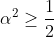
En utilisant la seconde équation, on peut prouver de la même manière que 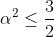et .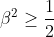
De fait :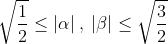
, et du fait de la croissance de la fonction sinus au carré, on a : 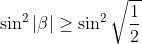. Et à cause de l'imparité de la fonction sinus et de la parité de la fonction carrée, il vient que 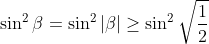. Appelons ce résultat : (3).
(2) implique que : 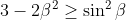, puis 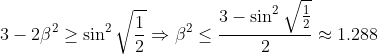, en utilisant (3).
On vient de passer de 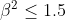à 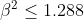, et on peut répéter ce processus autant de fois qu'on veut. A l'infini, on aura : .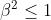
Semblablement, 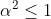. Et puisque (1), il vient que .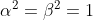
D'où finalement :

Bon voici une autre :
on a clairement :

Si |x|>|y| donc :

Donc :
1>|x|>|y| cad x²+y²<2 absurde ..
même raisonnement pour |y|>|x|
Donc |x|=|y| => |x|=|y|=1

Sylphaen a écrit:

Bon voici une autre :
on a clairement :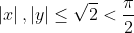

Si |x|>|y| donc :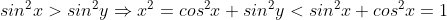

Donc :
1>|x|>|y| cad x²+y²<2 absurde ..
même raisonnement pour |y|>|x|
Donc |x|=|y| => |x|=|y|=1

Bravo. Du coup, c'est bien plus rigoureux que ma "démonstration".

Sylphaen a écrit:

Pour le 2 c'est m=3 et p=2
Posons :

Donc :



Donc :
pm=6
avec une disjonction de cas sur IN on trouve finalement p=2 et m=3
..
Sauf erreur ..

x est supposé appartenir à l'ensemble des rationnels, plutôt qu'à l'ensemble des naturels.

Slt Dijkcacheiner , comment va tu ?

Je trouve ta solution plus beau , mais un peu longue , Bien fait et parfait.