| | Olympiade de Kénitra (2nd tour) |  |
|
+4master M.Marjani W.Elluizi Dijkschneier 8 participants |
|
| Auteur | Message |
|---|
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Olympiade de Kénitra (2nd tour) Sujet: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 18:01 Ven 14 Mai 2010, 18:01 | |
| Exercice 1 :Soit a et b des réels. Résoudre dans  l'équation : 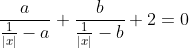 Exercice 2 : Exercice 2 :Soit x et y des réels strictement positifs et soit 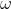 le minimum des trois nombres : 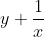 ,  et  Prouvez que : 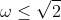 Exercice 3 : Exercice 3 :Résoudre dans 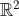 le système : (x-y^2)=1%20\end{cases}) Exercice 4 : Exercice 4 :Soit x, y et z des nombres réels tels que :  Montrez que : ^2}+\frac{y}{(z-x)^2}+\frac{z}{(x-y)^2}=0) Exercice 5 : Exercice 5 :Soit un n un entier naturel non nul. On considère l'ensemble 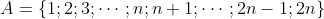 contenant tous les entiers naturels compris entre 1 et 2n. On choisit n elements 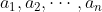 de l'ensemble A tels que : 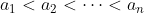 , et n éléments 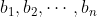 de l'ensemble A tels que : 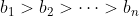 , avec 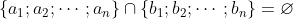 . Montrez que : 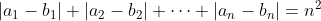 Exercice 6 : Exercice 6 :Soit ABCD un quadrilatère dont les diagonales sont perpendiculaires. Montrez que les droites perpendiculaires respectivement à (BC) et à (DC) et passant respectivement par les milieux de [AD] et [AB] se coupent en un point faisant parti de la droite (AC).
Dernière édition par Dijkschneier le Ven 14 Mai 2010, 18:56, édité 1 fois | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 18:12 Ven 14 Mai 2010, 18:12 | |
| Vous venez juste de passer le 2eme Touur??! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 18:18 Ven 14 Mai 2010, 18:18 | |
| Le 0eme tour a été une compétition que nous avions passé au sein de l'établissement, dont le but était de sélectionner les élèves éligibles à participer aux vrais tours d'olympiades, et que je ne compte naturellement pas.
Ce que j'appelle le second tour est le dernier tour des olympiades académiques organisés à Kénitra, et qui a lieu le 14 mai 2010. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 18:19 Ven 14 Mai 2010, 18:19 | |
| BJR Mr Dijcka. Le méme Olymp que j'ai passé.
J'ai fais 4/6, un EX je doute..
T'as compléter tout l'exercises Dijcka en 3h ?
Dernière édition par M.Marjani le Ven 14 Mai 2010, 18:20, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 18:20 Ven 14 Mai 2010, 18:20 | |
| - M.Marjani a écrit:
- BJR Mr Dijcka. Le méme Olymp que j'ai passé.
J'ai fais 4/6, un EX je doute.. Bravo ! Mais vous aviez passé au sein de quel établissement ? | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 18:21 Ven 14 Mai 2010, 18:21 | |
| - Dijkschneier a écrit:
- M.Marjani a écrit:
- BJR Mr Dijcka. Le méme Olymp que j'ai passé.
J'ai fais 4/6, un EX je doute.. Bravo ! Mais vous aviez passé au sein de quel établissement ? Lycée Sidi Aissa > Souk Larbaa. je poste mes soluces quand je re. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 18:26 Ven 14 Mai 2010, 18:26 | |
| - M.Marjani a écrit:
- T'as compléter tout l'exercises Dijcka en 3h ?
3 heures ont été à mon sens largement suffisantes. Je n'ai pas abordé le cinquième exercice très rigoureusement. Mes solutions concernant les cinq autres doivent être correctes. | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 19:02 Ven 14 Mai 2010, 19:02 | |
| slt , bonne olympiade , pas facile et meme pas difficile :
pour cinquiéme exo :
supposons bi>ai (i£{1,2,3......,n})
puisque {a1,a2,....,an}^ {b1,b2,b3.....,bn}=vide
donc l'ensemble A ={1,2,3,....,a1,a2,.....an,b1,b2,......,bn,....2n}
donc on deduit qu'il ya n élément entre a1 et b1
de meme a2 et b2 et .......... et n element entre an et bn!!
donc |a1-b1|=n et |a2 - b2|=n ..........et |an - bn|=n
donc |a1 - b1| + |a2 - b2|+.......+|an - bn|=n+n+.....+n (n fois) =n.n=n² | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 19:24 Ven 14 Mai 2010, 19:24 | |
| - master a écrit:
- slt , bonne olympiade , pas facile et meme pas difficile :
pour cinquiéme exo :
supposons bi>ai (i£{1,2,3......,n})
puisque {a1,a2,....,an}^ {b1,b2,b3.....,bn}=vide
donc l'ensemble A ={1,2,3,....,a1,a2,.....an,b1,b2,......,bn,....2n}
donc on deduit qu'il ya n élément entre a1 et b1
de meme a2 et b2 et .......... et n element entre an et bn!!
donc |a1-b1|=n et |a2 - b2|=n ..........et |an - bn|=n
donc |a1 - b1| + |a2 - b2|+.......+|an - bn|=n+n+.....+n (n fois) =n.n=n² Ton raisonnement ne tient pas du tout debout. Pourquoi ? Pour plusieurs points : - Tu ne peux pas supposer que bi>ai pour tout i£{1,2,3......,n}, car ces nombres sont piochés aléatoirement, et tu ne peux pas forcément y ajouter une contrainte de la sorte. - donc on deduit qu'il ya n élément entre a1 et b1 => cela ne veut absolument rien dire ; on ne parle pas d'éloignement dans un ensemble. - |a1-b1|=n => absolument pas ; tu peux très bien construire deux suites a_n et b_n pour lesquelles cette égalité n'est pas correcte du tout. | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 19:34 Ven 14 Mai 2010, 19:34 | |
| pour premier point , c pas meme interessant de les supposer je l'ai just ajouter car tjr |ai - bi| reste postif ce qui est interessant !
deuxiéme point c fait pour éclairée 3 point ! puisque il y en a n élément entre a et b ! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 19:47 Ven 14 Mai 2010, 19:47 | |
| Le plus facile est celui-ci: Résoudre dans 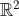 le système : (x-y^2)=1\end{cases}) . Après la précision du domaine de définition, chose très facile, on procède de suit: Donc (x-y^2)}=1\end{cases}) . Donc (x-y^2)}=1\end{cases}) . Posons 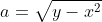 et 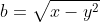 . Notre système équivaut à 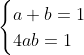 . Donc 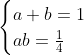 . Donc a et b sont les solutio de l'équation 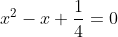 . Soit 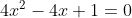 . Donc ^2-2*2x+1=0) . Donc ^2=0) . Donc 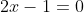 . Donc 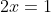 . Donc 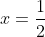 . Donc 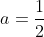 et 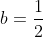 . Donc 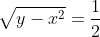 et 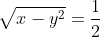 . Pour trouver x et y, on est amené à résoudre le système: 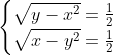 . Donc ^2=(\frac{1}{2})^2\\(\sqrt{x-y^2})^2=(\frac{1}{2})^2\end{cases}) . Donc 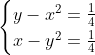 . En sommant ces deux lignes, on trouve 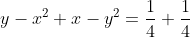 . Donc 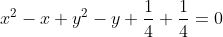 . Donc 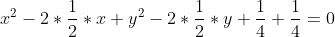 . Donc ^2+(y-\frac{1}{2})^2=0) . Donc ^2=0) et ^2=0) . Donc 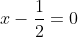 et 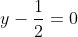 . Donc 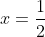 et 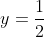 . Donc ) . Sauf erreur. | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 20:00 Ven 14 Mai 2010, 20:00 | |
| - nmo a écrit:
- Le plus facile est celui-ci:
Résoudre dans 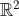 le système : le système :
(x-y^2)=1\end{cases}) . .
Après la précision du domaine de définition, chose très facile, on procède de suit:
Donc (x-y^2)}=1\end{cases}) . .
Donc (x-y^2)}=1\end{cases}) . .
Posons 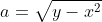 et et 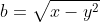 . .
Notre système équivaut à 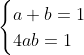 . .
Donc 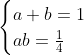 . .
Donc a et b sont les solutio de l'équation 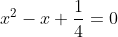 . .
Soit 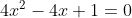 . .
Donc ^2-2*2x+1=0) . .
Donc ^2=0) . .
Donc 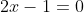 . .
Donc 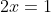 . .
Donc 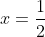 . .
Donc 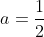 et et 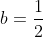 . .
Donc 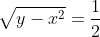 et et 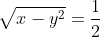 . .
Pour trouver x et y, on est amené à résoudre le système:
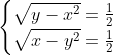 . .
Donc ^2=(\frac{1}{2})^2\\(\sqrt{x-y^2})^2=(\frac{1}{2})^2\end{cases}) . .
Donc 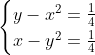 . .
En sommant ces deux lignes, on trouve 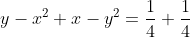 . .
Donc 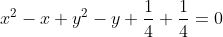 . .
Donc 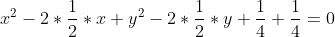 . .
Donc ^2+(y-\frac{1}{2})^2=0) . .
Donc ^2=0) et et ^2=0) . .
Donc 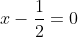 et et 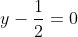 . .
Donc 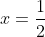 et et 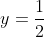 . .
Donc ) . .
Sauf erreur. Pourquoi tout cela? c'est bien une solution, mais il existe d'autre bcp plus mieux, par exemple si tu pose a=V(y-x²) et b=V(x-y²) tu trouvera que a+b=1 et ab=1/4 avec bien sur a,b>0, or on sait deja que ab=<14(a+b)²=1/4, et qu'elle n'atteint cette valeur que lorsque a=b=1/2 i.e: x-y²=y-x²=1/4, x-y²=y-x² <=> (x-y)(x+y+1)=0 => x=y ou x+y=-1cas (2) => x-(x+1)²=1/4 <=> (x+1)²+1/4=x , imposile car (x+1)²>xcas (2) =>x²-x+1/4=0 => (x,y)=(1/2,1/2).Remarque: l'exo 5 semble etre interessent! en tout cas je vous espere bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 20:07 Ven 14 Mai 2010, 20:07 | |
| Pour le premier: On a 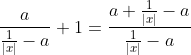 . Donc 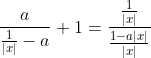 . Donc 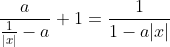 . De même 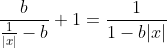 . Donc 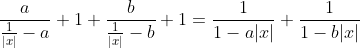 . Donc 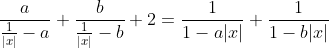 . Donc 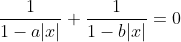 . Donc 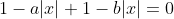 . Donc |x|=0) . Donc |x|) . Donc 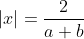 . Donc 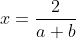 ou 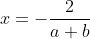 . Donc 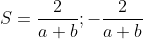 . Sauf erreur. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 20:18 Ven 14 Mai 2010, 20:18 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 20:27 Ven 14 Mai 2010, 20:27 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 14 Mai 2010, 22:42 Ven 14 Mai 2010, 22:42 | |
| J'ai fais méme methode qu'a fait Nmo au premier EX.
Et 3éme EX j'ai trouver la méme solution, je l'ai fais avec Delta qui égale à 0 <=> x=-b/2a=1/2
Exercice 4: Je l'ai fais par symétrie de roles. a>=y>=z, on trouve que la premiére equation >=0 et dans les donnés =0, et la deuxiéme equation qu'on veut démontrer >=0..
EX5: Il ne me reste plus de temps pour le faire (Surtout qu'on a commencer à 3.00 h et sortant à 5.40 ..
EX6: Il suffit de remarquer que: les deux hauteurs sont en méme temps (متوسطات), je l'ai fais par les triangles ressemblable et les projections.
Sinon on peut utiliser la reccurence, en supposons qu'ils se coupent en M, puis On utilise La Multiplication Scalaire pour trouver que: les deux droites perpendiculaires à (AD) et (AB)..
PS: Comme ils ont dis, le 5éme EX est plus intéressent, je vais faire un essaie pour le résoudre. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Sam 15 Mai 2010, 12:26 Sam 15 Mai 2010, 12:26 | |
| - M.Marjani a écrit:
- Exercice 4: Je l'ai fais par symétrie de roles. a>=y>=z, on trouve que la premiére equation >=0 et dans les donnés =0, et la deuxiéme equation qu'on veut démontrer >=0..
Merci d'étaler cette méthode qui semble prometteuse. - M.Marjani a écrit:
- EX6: Il suffit de remarquer que: les deux hauteurs sont en méme temps (متوسطات), je l'ai fais par les triangles ressemblable et les projections.
De dire qu'il suffit de faire la remarque que tu as précisée n'est pas très honnête ; aussi se veut-il que vous en donniez une preuve déployée. - M.Marjani a écrit:
- Sinon on peut utiliser la reccurence, en supposons qu'ils se coupent en M, puis On utilise La Multiplication Scalaire pour trouver que: les deux droites perpendiculaires à (AD) et (AB)..
La récurrence ? La multiplication scalaire ? Mais quel pathos fuligineux ! Vous me rappelez l'histoire des gens qui disent que pour démontrer une inégalité donnée, il suffit d'utiliser IAG+CS+Jensen+Muirhead+Karamata, et le tour est joué. Merci d'être plus concis et d'apporter des preuves plutôt que de rire sur le dos des gens. Faisons un effort pour être honnête dans nos interventions. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Sam 15 Mai 2010, 12:37 Sam 15 Mai 2010, 12:37 | |
| BJR Mr Dijcka.. Vous semblez que vous avez l'air nerveux  . Bon Tu peut partir par ce qu'il on veut démontrer pour trouver les droites qui sont perpenduculaires. Regarde ce poste tu vas comprendre comment: ------------------------------------------------------------------------------- EX:5: abc un triangles isocèle en A : I منتصف [bc] et h المسقط العمودي de I sur ( ac ) et J منتصف [IH] démontrez que (AJ) et (BH) sont perpendiculaires . -------------------------------------------------------------------------------- BJR!! Merci bien Mim pour l'épreuve !! Je pense que l'olymp n'est pas difficile et n'est pas façile Voilà mon premiére essaie avec le quatriéme: On va utiliser la multiplication scalaire: (tout est vecteurs) ----------------------------------------------------------------------- On va utiliser: (vecteurs) AC.IH=0 (car (AC) et (IH) sont perpendiculaires. On a: AJ.BH=(AC+CJ)(BI+IH)=AC.BI+CJ.BI+CJ.IH => AJ.BH=AC.IC+(CH+HJ).IC+(CH+HJ).IH => AJ.BH=AC.HC+(CH+HJ)(IH+HC)+HJ+IH => AJ.BH=AC.HC+CH.HC+HJ.IH+HJ.IH => AJ.BH=AC.HC-CH²+2HJ.IH => AJ.BH=AC.HC-CH²-IH² => AJ.BH=AC.HC-IC² => AJ.BH=(sans vecteurs)CH*CA-IC² [CH et CA ont le méme sense] Et souvent (العلاقات المترية) dans le triangle AIC On a: CH*CA-IC²=0 Donc: => AJ.BH=0 Il en résulte donc que: (AJ) et (BH) sont perpendiculaires. CQFD. -------------------------------------------------------------------------------- Pour moi j'ai pas fais fais cette methode, mais j'ai supposer qu'on peut l'utiliser (Surement qui est expert en maths peut la prouver.) + Pour la geométrie, je vais poster ma solution aprés mon retour. Bonne courage.
Dernière édition par M.Marjani le Sam 15 Mai 2010, 19:49, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Sam 15 Mai 2010, 19:48 Sam 15 Mai 2010, 19:48 | |
| Désolé pour mes termes que j'utilise, je n'ai aucun idée sur la réccurence mais ce que je veut dire est clair d'aprés mon deuxiéme poste. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Sam 15 Mai 2010, 20:53 Sam 15 Mai 2010, 20:53 | |
| L'exercice 4 a l'air facile, mais qui est trop dur. Bon, voilà ce que j'ai fait: On a  . Donc \big(\frac{1}{y-z}+\frac{1}{z-x}+\frac{1}{x-y}\big)=0*\big(\frac{1}{y-z}+\frac{1}{z-x}+\frac{1}{x-y}\big)) . Donc ^2}+\frac{x}{(z-x)(y-z)}+\frac{x}{(x-y)(y-z)}+\frac{y}{(z-x)(y-z)}+\frac{y}{(z-x)^2}+\frac{y}{(z-x)(x-y)}+\frac{z}{(x-y)(y-z)}+\frac{z}{(x-y)(z-x)}+\frac{z}{(x-y)^2}=0) . Donc ^2}+\frac{y}{(z-x)^2}+\frac{z}{(x-y)^2}+\frac{x}{(z-x)(y-z)}+\frac{y}{(z-x)(y-z)}+\frac{z}{(x-y)(y-z)}+\frac{x}{(x-y)(y-z)}+\frac{y}{(z-x)(x-y)}+\frac{z}{(x-y)(z-x)}=0) . Donc ^2}+\frac{y}{(z-x)^2}+\frac{z}{(x-y)^2}+\frac{x+y}{(z-x)(y-z)}+\frac{z+x}{(x-y)(y-z)}+\frac{y+z}{(z-x)(x-y)}=0) . Donc ^2}+\frac{y}{(z-x)^2}+\frac{z}{(x-y)^2}+\frac{(x+y)(x-y)}{(z-x)(y-z)(x-y)}+\frac{(z+x)(z-x)}{(x-y)(y-z)(z-x)}+\frac{(y+z)(y-z)}{(z-x)(x-y)(y-z)}=0) . Donc ^2}+\frac{y}{(z-x)^2}+\frac{z}{(x-y)^2}+\frac{x^2-y^2}{(z-x)(y-z)(x-y)}+\frac{z^2-x^2}{(x-y)(y-z)(z-x)}+\frac{y^2-z^2}{(z-x)(x-y)(y-z)}=0) . Donc ^2}+\frac{y}{(z-x)^2}+\frac{z}{(x-y)^2}+\frac{x^2-y^2+z^2-x^2+y^2-z^2}{(z-x)(x-y)(y-z)}=0) . Donc ^2}+\frac{y}{(z-x)^2}+\frac{z}{(x-y)^2}+\frac{0}{(z-x)(x-y)(y-z)}=0) . Donc ^2}+\frac{y}{(z-x)^2}+\frac{z}{(x-y)^2}+0=0) . Donc ^2}+\frac{y}{(z-x)^2}+\frac{z}{(x-y)^2}=0) . CQFD. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Sam 15 Mai 2010, 21:01 Sam 15 Mai 2010, 21:01 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Sam 15 Mai 2010, 21:12 Sam 15 Mai 2010, 21:12 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Sam 15 Mai 2010, 21:23 Sam 15 Mai 2010, 21:23 | |
| - nmo a écrit:
A propos de l'exercice 5, les troncs communs n'ont pas encore étudier les ensemble.
On doit poser la question, pourquoi cet exercice est présent ici?
Mais bien sûr que si. Il suffit de connaître un peu ses cours pour s'en rendre compte. - nmo a écrit:
En plus pour l'exercice 6:
Si je ne me trompe pas, pour montrer que trois droites sont concourantes en un seul point il faut choisir un triangle convenable, puis on démontre que ces droites ne sont autres que les médianes ou les bissectrices ou les médiatrice ou les hauteurs.
J'attends ton avis.
Dans des problèmes différents, cela peut évidemment être une approche possible. Mais si vous aviez eu le soin de construire la figure, vous en conviendrez que l'on ne peut se fixer un seul triangle intéressant dans lequel ces droites là seront des céviennes (médianes, hauteurs, ...), et de ce fait, le problème n'est pas abordable de la sorte. J'ai personnellement construit mon raisonnement en jouant avec l'analyse, c-à-d en commençant par construire un repère orthonormé centré sur le le centre du quadrilatère. J'ai ouï dire par un forumiste qu'on pouvait utiliser le produit scalaire, et cela me semble envisageable, également.
Dernière édition par Dijkschneier le Mer 01 Sep 2010, 22:51, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Sam 15 Mai 2010, 21:57 Sam 15 Mai 2010, 21:57 | |
| [quote="Dijkschneier"] - nmo a écrit:
A propos de l'exercice 5, les troncs communs n'ont pas encore étudier les ensemble.
On doit poser la question, pourquoi cet exercice est présent ici?
Mais bien sûr que si. Il suffit de connaître un peu ses cours pour s'en rendre compte. --------------------------------------------------------------------------------- Pour vous oui donc. Mais pour nous le contraire(on a pas su de grands choses sur les ensembles)  Personellement quand j'ai vu l'exercise, tout ce que j'ai compris que a1,a1,...an se différent de b1,b2,...bn. Mais la question qui se pose était comment procéder en methode de T.C? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Dim 16 Mai 2010, 11:32 Dim 16 Mai 2010, 11:32 | |
| - nmo a écrit:
- Pour le premier:
On a 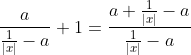 . .
Donc 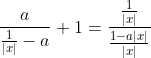 . .
Donc 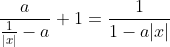 . .
De même 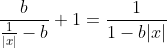 . .
Donc 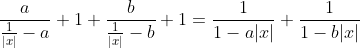 . .
Donc 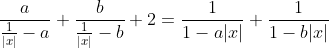 . .
Donc 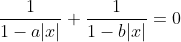 . .
Donc 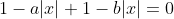 . .
Donc |x|=0) . .
Donc |x|) . .
Donc 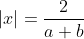 . .
Donc 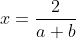 ou ou 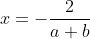 . .
Donc 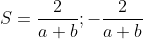 . .
Sauf erreur. - Dijkschneier a écrit:
- Cette fois-ci, peut-être par mégarde, tu n'as pas eu la lucidité de préciser le domaine de définition. De préciser le domaine de définition a une importance cruciale car ça apporte des contraintes supplémentaires dans la résolution.
Vous n'aviez pas semblé prendre ma remarque avec un air d'intérêt, alors laissez-moi vous montrer explicitement votre faute. Résolvons l'équation 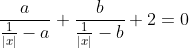 L'équation est définie ssi 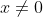 et 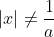 et 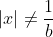 Et l'équation est équivalente à +b(\frac{1}{|x|}-a)+2(\frac{1}{|x|}-a)(\frac{1}{|x|}-b)}{(\frac{1}{|x|}-a)(\frac{1}{|x|}-b)}=0) Ou encore à =0) C'est-à-dire 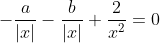 Ou bien }{x^2}=0) Ainsi =2) - Si a=-b ou a=b=0, alors manifestement, 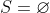 - Si 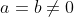 , alors 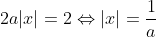 . Mais l'équation n'est pas définie dans ce cas, donc 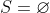 - Sinon, 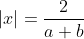 , et donc 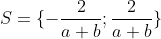 Synthèse : - Si 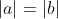 , alors 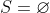 - Si 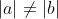 , alors 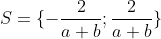 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  | |
| |
|
  | |
| | Olympiade de Kénitra (2nd tour) |  |
|
