Olympiade de Kénitra (1er tour)

Exercice 1 :
Soit x et y des réels strictement positifs.
Montrer que : .

Exercice 2 :
Soit P(x) un polynôme tel que : .
Soit a,b et c les racines de ce polynôme.
Montrer que : 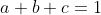et .

Exercice 3 :
Résoudre l'équation suivante dans : .

Exercice 4 :
Discuter selon les valeurs du paramètre m les solutions de l'inéquation : .

Exercice 5 :
1) Soit MNP et MNP' deux triangles tels que . Montrer que les deux triangles ont la même surface.
2) Une laborieuse application de 1)

EDIT : Finalement, le premier exercice était bel et bien faux. Ici est présentée la version corrigée.

Remarquant la fausseté du premier exercice, j'ai fait, dans les premières minutes, la remarque au surveillant, qui, entêté, a obstinément réfuté ma remarque.
Est-il faux ? Vrai ? Va savoir !

bsr
exo1: d'apres IAG

x(1+1/y²) + y(1+1/x²)=x+x/y² + y+y/x² >= 4 V(x²y²/x²y²)=4

Slt Dijk ))

Le méme Oly qu'ils nous ont donné.

J'ai fais les deux premiéres exercices en 20 minutes , le troisiéme en 20 min , et je pense pas qu'il ya une faute Mr dejkcheiner ..
je peux poser ma réponse de ce dernier ?

le quatriéme ex , ya un truc là j'ai pas arrivé à trouver ce truc , mais j'ai fais le cas de m=0 .. les autres cas c'est trop compliqué.

le 5éme EX la premiére qustion c'est facile .. On va utiliser les largeurs ( h ) qui se répertorié dans un trapèze , la deuxiéme question ayaye , mais j'ai remarqué que le quatriéme rectangle , on peut le deviser de la maniére suivante : chaque 1/4 d'un coté , on la relie avec le 1/4 de coté opposé ! de la méme maniere avec les deux autres cotés qui s'oppose au rectangle.

Vous obtiendrez des petites parallélogrammes au rectangle ! alors on peut trouver la surface d'un POLYGONAL au moins !

MohE a écrit:

encore il font des faut aux olympiades, pfff! c'est toujours nul, il faudra un 1 à la place de x.
P.S: je crois que l'olymp etait facile, je doute pas que tu as bien travailler Dijkschneier!

Slt Mr MoH , je vois aucune faute dans l'enigalité , on peut dire que x>0

x²>x alors on va remplacer le x² avec le x dans l'inigalité aprés a²+b²>=2ab ! , je peux poser ma réponse ?

exo2:
d'abord on suppose que A=alpha et B=beta car je ne peux pas ecrire en latex!!!

puisque a et b et c sont les racings du polynome alors:
Aa^3 - Aa² + Ba+B=Ab^3-Ab²+Bb+B =0 (*)
et Ab^3-Ab²+Bb+B = Ac^3 -Ac²+Bc+B =0 (**)
avec (*) on deduit que: a=b ou B=A(a²+b²+ab-a-b)
et par (**) on distingue : c=b ou B=A(c²+b²+cb-c-b)
ce qui prouve que a²+ab-a=c²+cb-c
donc on aurait que a+b+c=1

exo3:
pour ce exo je l'ai fait mais vraiment j'ai un probleme avec latex mais ma solution est S=1

master a écrit:

exo2:
d'abord on suppose que A=alpha et B=beta car je ne peux pas ecrire en latex!!!

puisque a et b et c sont les racings du polynome alors:
Aa^3 - Aa² + Ba+B=Ab^3-Ab²+Bb+B =0 (*)
et Ab^3-Ab²+Bb+B = Ac^3 -Ac²+Bc+B =0 (**)
avec (*) on deduit que: a=b ou B=A(a²+b²+ab-a-b)
et par (**) on distingue : c=b ou B=A(c²+b²+cb-c-b)
ce qui prouve que a²+ab-a=c²+cb-c
donc on aurait que a+b+c=1

Slt Mr Master , Bonne solution , je pense que t'as bien travaillé dans ce Oly :O , bon courage , Vous serez qualifiez tous ncha2 lah ))

master a écrit:

exo3:
pour ce exo je l'ai fait mais vraiment j'ai un probleme avec latex mais ma solution est S=1

T'as fais une seul solution Mr Master ))

Car , il ya deux solution , x=1 et x=4 ^^

ahaa , pourquoi ? : > Racine(1-2racine x+x) = |racine x - 1|

mais pas grave .

))

M.Marjani a écrit:

MohE a écrit:

encore il font des faut aux olympiades, pfff! c'est toujours nul, il faudra un 1 à la place de x.
P.S: je crois que l'olymp etait facile, je doute pas que tu as bien travailler Dijkschneier!

Slt Mr MoH , je vois aucune faute dans l'enigalité , on peut dire que x>0

x²>x alors on va remplacer le x² avec le x dans l'inigalité aprés a²+b²>=2ab ! , je peux poser ma réponse ?

x>0 <=> x²>x ? C'est faux. x>1 plutôt.

mizmaz a écrit:

M.Marjani a écrit:

MohE a écrit:

encore il font des faut aux olympiades, pfff! c'est toujours nul, il faudra un 1 à la place de x.
P.S: je crois que l'olymp etait facile, je doute pas que tu as bien travailler Dijkschneier!

Slt Mr MoH , je vois aucune faute dans l'enigalité , on peut dire que x>0

x²>x alors on va remplacer le x² avec le x dans l'inigalité aprés a²+b²>=2ab ! , je peux poser ma réponse ?

x>0 <=> x²>x ? C'est faux. x>1 plutôt.

, plutôt.

M.Marjani a écrit:

master a écrit:

exo3:
pour ce exo je l'ai fait mais vraiment j'ai un probleme avec latex mais ma solution est S=1

T'as fais une seul solution Mr Master ))

Car , il ya deux solution , x=1 et x=4 ^^

ahaa , pourquoi ? : > Racine(1-2racine x+x) = |racine x - 1|

mais pas grave .

))

Il y a tout l'intervalle compris entre 1 et 4 qui est solution à l'équation.

mizmaz a écrit:

M.Marjani a écrit:

MohE a écrit:

encore il font des faut aux olympiades, pfff! c'est toujours nul, il faudra un 1 à la place de x.
P.S: je crois que l'olymp etait facile, je doute pas que tu as bien travailler Dijkschneier!

Slt Mr MoH , je vois aucune faute dans l'enigalité , on peut dire que x>0

x²>x alors on va remplacer le x² avec le x dans l'inigalité aprés a²+b²>=2ab ! , je peux poser ma réponse ?

x>0 <=> x²>x ? C'est faux. x>1 plutôt.

Oui t'as raison , alors le premier EX eleminé ou quoi ? Opss .. autre fois de grands errors.

j'aime bien les gens qui se prennent pour des génies et qui se la prennent en plein tranche aprés hh ( moi je dis sa comme sa je parle de personne en particulier ^^ )

darkpseudo a écrit:

j'aime bien les gens qui se prennent pour des génies et qui se la prennent en plein tranche aprés hh ( moi je dis sa comme sa je parle de personne en particulier ^^ )

Ok , le sujet c'est autour l'oly je pense

darkpseudo a écrit:

j'aime bien les gens qui se prennent pour des génies et qui se la prennent en plein tranche aprés hh ( moi je dis sa comme sa je parle de personne en particulier ^^ )

T'as déjà ... et la réaction était comme ca :

the kiler a écrit:
o zaydon so9 khtak fya?




je vais pas faire le saint entre les diables ; mais sa serais gentil d'enlever cette phrase stp , car elle sali un peu le forum !!
+ je sais bien que tu le fais pas exprés the kiler ( et au fait j'ai adorer ta méthode du deuxiéme exo )
mais quand tu poste stp essaie de ne pas faire de poste successif tu n'aura qu'as moderer ton post et y ajouter ce que tu veux dire ; et merci ^^

https://mathsmaroc.jeun.fr/premiere-f5/3eme-test-d-olympiade-t15492.htm

Un peu de respect svp , là on discute autour d'Oly , nous nous battons pas ( je pense )

Je vous remercie Mr Dark pour la bonne réception

Je vois qu'il y a deux exercices qui sont un peu difficile, le quatrième et le dernier.
Je vais répondre sur tout les exrcices dont je sais la réponse dans mes prochains messages.
Pour le premier, c'est tellement faux comme a été déja annoncé.

Pour le deuxième:
On sait que a, b, et c sont des racines au polynome P.
Donc on peut écrire P(x)=(x-a)(x-b)(x-c).
Donc P(x)=x^3-(a+b+c)x^2+(ab+ac+bc)x-abc.
Et on a P(x)=alphax^3-alphax^2+bêtax+bêta=0.
Donc a+b+c=alpha et 1=alpha et ab+ac+bc=bêta et abc=-bêta.
Donc a+b+c=1 et (ab+ac+bc)/abc=(bêta)/(-bêta).
Donc a+b+c=1 et ab/abc + ac/abc + bc/abc=-1.
Donc a+b+c=1 et 1/c+1/b+1/a=-1.
CQFD.

nmo a écrit:

Pour le deuxième:
On sait que a, b, et c sont des racines au polynome P.
Donc on peut écrire P(x)=(x-a)(x-b)(x-c).

, plutôt.

Pour le troisième:
On veut résoudre l'équation:V(x-2Vx+1)+V(x-4Vx+4)=1.
Donc V(Vx^2-2*Vx*1+1^2)+V(Vx^2-2*Vx*2+2^2)=1.
Donc V[(Vx-1)^2]+V[(Vx-2)^2]=1.
Donc |Vx-1|+|Vx-2|=1.
Le premier cas: Vx>=2.
Donc l'équation équivaut Vx-1+Vx-2=1.
Donc 2Vx=4.
Donc Vx=2.
Donc x=4.
Enfin S1=4.
Le deuxième cas: 2>=Vx>=1.
Donc l'équation équivaut Vx-1+2-Vx=1.
Donc 1=1.
Ce qui est juste.
Donc S2=[1;4] car 2>=Vx>=1.
Le troisième cas 1>=Vx.
Donc l'équation équivaut 1-Vx+2-Vx=1.
Donc 3-2Vx=1.
Donc 2Vx=2.
Donc Vx=1.
Donc x=1.
Enfin S3=3.
D'après S1 et S2 et S3, on déduit que S=[1;4].

Dijkschneier a écrit:

nmo a écrit:

Pour le deuxième:
On sait que a, b, et c sont des racines au polynome P.
Donc on peut écrire P(x)=(x-a)(x-b)(x-c).

, plutôt.

Donc k=1 dans notre cas.

Je cherche encore pour le quatrième, et je sais la solution du dernier, mais avant de la poster, dessine la figure car je ne sais pas comment faire.

nmo a écrit:

Dijkschneier a écrit:

, plutôt.

Donc k=1 dans notre cas.

Basiquement, , dans notre cas.

nmo a écrit:

Je cherche encore pour le quatrième, et je sais la solution du dernier, mais avant de la poster, dessine la figure car je ne sais pas comment faire.

Le dernier exercice a été proposé tel quel, c-à-d, non accompagné par une figure. Le candidat devait se démerder.

Dijkschneier a écrit:

mizmaz a écrit:

M.Marjani a écrit:

MohE a écrit:

encore il font des faut aux olympiades, pfff! c'est toujours nul, il faudra un 1 à la place de x.
P.S: je crois que l'olymp etait facile, je doute pas que tu as bien travailler Dijkschneier!

Slt Mr MoH , je vois aucune faute dans l'enigalité , on peut dire que x>0

x²>x alors on va remplacer le x² avec le x dans l'inigalité aprés a²+b²>=2ab ! , je peux poser ma réponse ?

x>0 <=> x²>x ? C'est faux. x>1 plutôt.

, plutôt.

Bah non, puisque x²>x et non x²>=x. =]
Au plaisir !

Citation :

Bah non, puisque x²>x et non x²>=x. =]
Au plaisir !

Posant 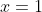, l'inégalité de départ équivaut à :
L'inégalité demeure donc juste.