inequalities !!

Prouvez lé inégalités suivantes:

________________________________________________________

a,b,c >=0



________________________________________________________

x+y+z=1 (x;y;z)>0



________________________________________________________

a,b,c>0 6>=a+b+c>=3



________________________________________________________

x,y,z>0 x+y+z=3



________________________________________________________

1)
elle équivaut à: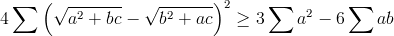


<=>:


<=> :

mais :

donc il suffit de montrer que:


ona :


en multipliant par sum(a²)+sum(ab) l'inégalité devient:
ce qui est clairement vrai ( sauf erreur)
A suivre

1)

On peut supposer que a >= b >= c,il est facile de prouver que : 2V(b²+ac) + 2V(c²+ab) =< 2V(2b²+2c²+2ab+2ac)

Il suffit de prouver alors que:

2V(2b²+2c²+2ab+2ac) + 2V(a²+bc) =< 3(a+b+c);

Après élévation au carré,elle devient:

(a-b-c)² + 20bc >= 12(a+b+c)( V(a²+bc) - a)

Il est facile de prouver que : V(a²+bc) - a =< bc/2a,

Par conséquent,il suffit de prouver que:

(a-b-c)² + 2bc + 6bc(2a-b-c)/a >= 0 ce qui est claire puisce que 2a >= b+c

( l'idée de la preuve devient claire après avoir remarqué que l'égalité a lieu quand l'un des variables égal à 0 et les deux autres sont égaux )

(1)

on a par CS


il suffit donc de Prouvez que:





on pose a+b+c=p et ab+bc+ca=q et abc=r

L'inégalité devient :



L'inégalité initiale est homogène on peut supposer que a+b+c=1
donc l'inégalité devient:



on a clairement r=<q^2/3

il suffit de montrer que :



ce qui est vrai puisque 0<q<1/3

rachid18 a écrit:

1)On peut supposer que a >= b >= c,il est facile de prouver que : 2V(b²+ac) + 2V(c²+ab) =< 2V(2b²+2c²+2ab+2ac)
[/b] )

je crois que cette preuve est connue...

et pr einsteinium la derniere inégalité est clairement fausse juste fais tendre q vers 0

je vais poster demain incha2alla la solution du deuxieme inégalité (que j'ai bien apprécié ) dans un document pdf
A+

neutrino a écrit:

et pr einsteinium la derniere inégalité est clairement fausse juste fais tendre q vers 0

oui tu as raison pffffffff je me suis trompé lors de mon calcul de delta.

je vais essayer de rectifier ce que je peux !!!

neutrino a écrit:

je crois que cette preuve est connue...

Peut etre,mais assure toi que j'ai réussi à trouver la preuve par moi meme avant de la chercher ailleurs => je m'en fou si la preuve soit connue ou pas

Amicalement

DSL pour le retard,j'ai un problème de connexion ces quatre derniers jours.Bon,voici ma preuve pour la quatrième inégalité:

4)

Cas 1: z=0

on a x+y=3 et on doit prouver que x²y =< 4 <=> x^3 + 4 - 3x² >= 0 <=> (x-2)²(x+1) >= 0 ce qui est vrai !

Cas 2: z différent de 0

Posons x+z = 3-y = a < 3,

L'inégalité devient:

a²z - a( x² + 6z + 3xz/2 ) + 3x² + 9z + 9xz/2 =< 4

En calculant le discriminant du terme à gauche on remarque qu'il est égal à x²(x + 3z/2)²,l'inégalité est alors équivalente à :

(3-a)(2x² + xz + 6z - 2z²) =< 8

Ou aussi:

(3-a)(-x² + x(5a-6) + 6a-2a²) =< 8

ce qui est équivalent à:

x²(3-a) + (3-a)(6-5a)x - (2a^3 - 12a² + 18a - 8 ) >= 0,

Le discriminant du polynome P(x)= x²(3-a) + (3-a)(6-5a)x - (2a^3 - 12a² + 18a - 8 ) égal à (3-a)(a-2)²(19-17a) ( facile à obtenir en remarquant que 2 et 3 sont des racines du polynome P(a)=(a-3)²(5a-6)² + 4(3-a)(2a^3-12a²+18a-8 ) ),

(*) Si a >= 19/17 : alors le discriminant du polynome P(x)= x²(3-a) + (3-a)(6-5a)x - (2a^3 - 12a² + 18a - 8 ) est inférieur ou égal à 0 et 3-a > 0 d'ou le résultat !

(*) Si a =< 19/17 : remarquer que P(x)=x²(3-a) + (3-a)(6-5a)x + 2(a-1)²(4-a);les coefficients de ce polynome sont tous positifs et x >= 0 alors P(x) >= 0 d'ou la conclusion !