Olympiodiose

J'ai l'honneur de vous annoncer le début de notre petit jeu:
Il s’agit de poster des exercices d’olympiade pour se préparer à l’olympiade, et surtout améliorer notre niveau en mathématique.
Les Conditions de participation sont faciles :
1-Poster le problème en indiquant son numéro comme l’exemple en bas.
2- Poster le problème et la solution en latex (ceux qui ne savent pas écrire en latex voici un lien (http://www.codecogs.com/components/eqneditor/editor.php)
3- Celui qui a trouvé la solution automatiquement il poste un autre , mais si la solution n’est pas trouvé dans 48 H alors celui qui a poster le problème il nous donne sa solution et poster un autre.
Pour finir je vais commencer par un petit problème :

Problème 1:
a b c et d des nombres réél positif :
prouver que :

vaut mieux s'interesser à vos études,à vos cours,vous aurez jamais besoin de ces exercices d'omypiades en tant que lyciens! ce qui compte au bac,c'est votre maitrise de cours et non pas l'application de cauchez schwartz dans m'exercice que tu viens de poser! si jamais vous êtres onterssés par les olypiades,vous faites ça à l'été lorsque vous êtes pas suivis par un examen comme celui du bac!

Salut
premier c'est une bonne idée samix de faire ce genre de topic .
Pour radouane , vous avez raison il faut pas oublier nos étude ,mais il n'y a aucun mal de faire de temps en temps des exo d'olymp , tout en travaillons les autres matiers. je sais pas si ce topic terminera , mais je propose une solution à ce probleme ^^ on peux faire un temps limite à ce topic comme une semaine ou moins, j'attend vos avis lool

je poste comme meme la solution


avec cauchy shwary on trouve ( comme a dis radouane)

radouane_BNE a écrit:

vaut mieux s'interesser à vos études,à vos cours,vous aurez jamais besoin de ces exercices d'omypiades en tant que lyciens! ce qui compte au bac,c'est votre maitrise de cours et non pas l'application de cauchez schwartz dans m'exercice que tu viens de poser! si jamais vous êtres onterssés par les olypiades,vous faites ça à l'été lorsque vous êtes pas suivis par un examen comme celui du bac!

Je vous remercie pour votre belle remarque , mais vu que les olympiades des premieres auront lieu le 20 novembre donc comme Mr abdess avait bien dit ça ne fera pas de mal d'organiser un petit jeu pour s'échanger les exercices d'olympiade et enrichir notre conaissance en maths afin de se bien préparer pour le jour d'olymp. donc je suggère de laisser ce topic pendant un certain temps si vous êtes bien d'accord avec moi biensur (j'attends vos avis)
et merci

Problème 2
SVP expliquer "Cauchy-Schwarz"

bonne idee 7ta 7na 3ndna l olympiades nhar 19 f had chher
et merci beucoup

Salut ,

je vois que l'idée de Samix est super , pour moi je suis d'accord donc celui qui est interset pour participer a ce jeu pour se preparer au prochaine olympiade (4 decembre) fait signe sur ce topic .... Alllezz j'attend vos réponse pour commencer

radoune a raison les gars fau pa donner trop dimpportance au olympiade

j'ai pas dis que radouane n'a pas raison , mais si tu travaille un peux d'olympiade sa ne causera pas grand probleme , mais en faite on prepare juste pour la prochaine epreuve

excellente idée samix

a un nombre réel positif tels que :a^5+a^3+a≥3
MQ: a^6>=5

Pour ton exo est dèja posté voici le lien https://mathsmaroc.jeun.fr/premiere-f5/montrer-que-t13932.htm

On attend d'autre participant pour commencer le jeu

samix a écrit:

Pour ton exo est dèja posté voici le lien https://mathsmaroc.jeun.fr/premiere-f5/montrer-que-t13932.htm

On attend d'autre participant pour commencer le jeu

merci samix

Bsr bon bein voila la réponse ^^

a^5+a^3+a≥3
donc :2 a^5+2a^3+2a-1≥5
supposons que
a^6-2a^5-2a^3-2a+1≥0
donc : (a^3-a^2)^2-a^4-2a^3-2a+1 ≥ 0
(a^3-a^2)^2-(a^2+a)^2+a^2-2a+1 ≥ 0
(a^3-a^2)^2-(a^2+a)^2+(a-1)^2 ≥ 0
puisque a^5+a^3+a≥3 donc : a≥1
alrs : (a^3-a^2)^2-(a^2+a)^2+(a-1)^2 ≥ 0 est toujours juste !!
et ce qu'on a supposer est juste ; CQFD ^^

mercii samix pour l'exo

Bon bein voila je remonte le sujet avec une ptite inéquation ^^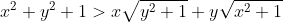
je donnerai la réponse demain soir si personne ne la fait ... Et j'en doute fort ^^

darkpseudo a écrit:

Bon bein voila je remonte le sujet avec une ptite inéquation ^^
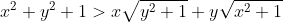
je donnerai la réponse demain soir si personne ne la fait ... Et j'en doute fort ^^

Ton inégalité est équivalente à : 1/2[(y-V(x²+1))²+(x-V(y²+1))²]>=0 ce qui est juste

voila , samix poste ton exo, mais stp exo simple dont la solution sant l'etulisation des relation hors programe.

Voila suite à ta demande un petit probleme

Problème:
a1,a2,a3,a4,a5,a6 des réel postif tel que: et
Montrer que :



J'éspere que le jeu continue

Bsr!!
on a
a_6.a_3>=a_1a_4+a_1a_5+a_2a_4+a_2a_5
V(a_6.a_3)>=V(a_1a_4+a_1a_5+a_2a_4+a_2a_5)
donc on doit montrer que :
V(a_1a_4+a_1a_5+a_2a_4+a_2a_5)>=V(a_1.a_4)+V(a_2.a_5)
<==>a_1a_5+a_2a_4>=2V(a_1.a_2.a_4.a_5)
ckyé vré !!

voila un ex ki a été posé ds la premiére épreuve de l 'olym l année dernier
x et y deux réels tels que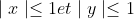
MQ

Merci les gar pour votre participation les 2 solution sont juste mais vu que juste-abdess qui a répondu le premier alors c'est ton tour de poster un exo on t'attends !

c pa grave s'il na pas postée un exo!?
en tous cas je l'ai fait à sa place

yassine-516 a écrit:

c pa grave s'il na pas postée un exo!?
en tous cas je l'ai fait à sa place

Non yassine lis les règles et pour ton inégalité elle est équivalent à :
0<= (y+1/2)²+(x+1/2)² <= 9/2 ce qui est juste parceque |x|<=1 et y<=1