| | Olympiodiose |  |
|
+31Dijkschneier SherlocK mizmaz reda-t smash stranger Emerson Perelman dima_amazigh Ayoub M-H EINSTEINIUM Sylphaen neohs noirouge majdouline soukki abdellah=einstein issam erriahi Thalès yassine-516 houssam110 marouan777 einstein20 darkpseudo albertmath otman1994 ayyoub Psi just-abdess radouane_BNE samix 35 participants |
|
| Auteur | Message |
|---|
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Dim 13 Juin 2010, 16:23 Dim 13 Juin 2010, 16:23 | |
| F.de frappe. C'est plutot R>=(a+b+c)/6 , et c'est réctifier.)) | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Dim 13 Juin 2010, 17:29 Dim 13 Juin 2010, 17:29 | |
| Seulement dans ce cas, toute votre démonstration s'écroule. Ce que vous dites : (a+b+c)/6>=(a+b+c)/3V3, est totalement faux. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Dim 13 Juin 2010, 17:40 Dim 13 Juin 2010, 17:40 | |
| - Seconde partie : Selon la loi des sinus : 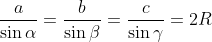 . Cela conduit à dire que : 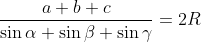 . Ainsi, l'inégalité est équivalente à : 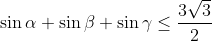 , qui est bien connue. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Dim 13 Juin 2010, 21:05 Dim 13 Juin 2010, 21:05 | |
| - Dijkschneier a écrit:
- Seulement dans ce cas, toute votre démonstration s'écroule. Ce que vous dites : (a+b+c)/6>=(a+b+c)/3V3, est totalement faux.
Oui, c'est plutot inférieur. A toi de poser le prochain EX. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Juin 2010, 11:29 Mar 15 Juin 2010, 11:29 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Juin 2010, 11:42 Mar 15 Juin 2010, 11:42 | |
| Pour démontrer que 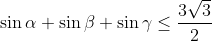 . La fonction sinus est concave sur ) . Donc, d'après l'inégalité de jensen }) . Donc }) . Donc 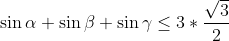 . CQFD. (Ce n'est pas ma methode). Pour démontrer celle-là plus siplement. Ces mesures appartiennent à ) . Donc leurs sinus est inférieurs de  . Soit en sommant 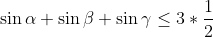 . Comme, 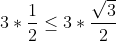 . Le résultat s'en découle. (C'est la methode que j'ai utilisé). | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Juin 2010, 11:52 Mar 15 Juin 2010, 11:52 | |
| C'est la méthode que vous aviez utilisé, mais elle est fausse. Parce que cela n'est pas correct : - Citation :
Ces mesures appartiennent à ) . .
Donc leurs sinus est inférieurs de  . . L'inégalité est assez forte, et lorsque vous dites : 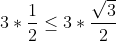 , vous laissez une marge très grande. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Juin 2010, 11:56 Mar 15 Juin 2010, 11:56 | |
| - Dijkschneier a écrit:
- C'est la méthode que vous aviez utilisé, mais elle est fausse.
Parce que cela n'est pas correct :
- Citation :
Ces mesures appartiennent à ) . .
Donc leurs sinus est inférieurs de  . . L'inégalité est assez forte, et lorsque vous dites : 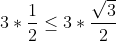 , vous laissez une marge très grande. , vous laissez une marge très grande. Logiquement, elle est juste. C'est à ça que j'ai pensé du début. Merci pour la remarque. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Juin 2010, 11:58 Mar 15 Juin 2010, 11:58 | |
| - Citation :
- Logiquement, elle est juste.
Pardon ? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Juin 2010, 11:59 Mar 15 Juin 2010, 11:59 | |
| - Dijkschneier a écrit:
-
- Citation :
- Logiquement, elle est juste.
Pardon ? On a a<b et b<c. Donc a<c. C'est logique, je pense. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mar 15 Juin 2010, 12:12 Mar 15 Juin 2010, 12:12 | |
| Voici une méthode juste avec am-gm sin(c)=sin(a+b)=sina.cosb+sinb.cosa Et on a : 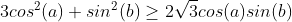 De même on trouve que : 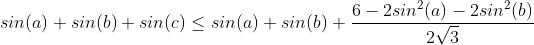 Donc il suffit de prouver que : 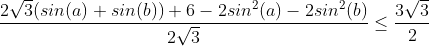 Qui est équivalente à : 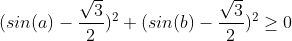 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Juin 2010, 10:12 Ven 18 Juin 2010, 10:12 | |
| Avant de terminer ce jeu, j'ai l'honneur de vous présenter l'ultime exercice: Trouvez tous les quadriplets des réels satisfaisant: -4(ab+cd)-6(b+2a)+46=0) . Bonne chance.P.S: J'attends vos remarques sur l'exercice ainsi que vos réponse. Car l'exercice est de ma propre création. Et je souhaite que le grand jeu d'été ait un énorme succés.
Dernière édition par nmo le Ven 18 Juin 2010, 10:34, édité 1 fois | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Juin 2010, 10:32 Ven 18 Juin 2010, 10:32 | |
| bonjour nmo je crois que c'est plutôt : c 4+5b²+2(a²+ d²)-4(ab+cd)-6(b+2a)+46=0 
Dernière édition par majdouline le Ven 18 Juin 2010, 10:54, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Juin 2010, 10:34 Ven 18 Juin 2010, 10:34 | |
| - majdouline a écrit:
- bonjour
nmo je crois que c'est plutôt :
c4+5d²+2(a²+b²)-4(ab+cd)-6(b+2a)+46=0
 Oui, j'ai une faute. Elle est soulignée. Au lieu de b c'est d. C'est édité maintenant. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Juin 2010, 10:51 Ven 18 Juin 2010, 10:51 | |
| donc j'aimerais bien réponde à l'ultime exo et mettre fin à ce jeu^^ on a : \in%20\mathbb%20R^2:c^4+d^2+d^2+1\geq%204cd) avec égalité si et seulement si (c,d)=(1,1);(-1,-1) et : \in%20\mathbb%20R^2:a^2+4b^2\geq%204ab) (avec égalité si et seulement si a=2b ) 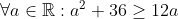 (avec égalité si et seulement si a=6) 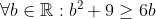 (avec égalité si et seulement si b=3) en sommant on aura : -4(ab+cd)-6(b+2a)+46\geq0) avec égalité si et seulement si a=3 et b=6 et (c,d)=(1,1);(-1,-1) conclusion S={(6,3,1,1);(6,3,-1,-1)} réciproquement ces solution vérifient l'équation! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Juin 2010, 11:13 Ven 18 Juin 2010, 11:13 | |
| Bravo majdouline, d'une autre manière: On a -4(ab+cd)-6(b+2a)+46=0) . Donc 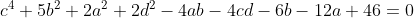 . Donc 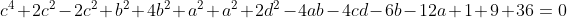 . Donc 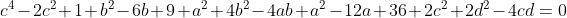 . Donc ^2+(b-3)^2+(a-2b)^2+(a-6)^2+2(c^2+d^2-2cd)=0) . Donc ^2+(b-3)^2+(a-2b)^2+(a-6)^2+2(c-d)^2=0) . Donc ^2=0) et ^2=0) et ^2=0) et ^2=0) et ^2=0) . Donc 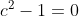 et 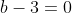 et 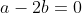 et 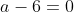 et 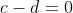 . Donc 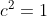 et 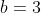 et 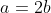 et 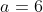 et 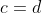 . Donc 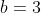 et 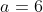 et 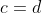 et 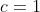 ou 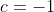 . On conclut que les quadriplets solutions sont: ;(3,6,-1,-1)\}) . Et c'est la fin de la démonstration ainsi que du jeu. | |
|
  | |
chamitos007
Maître

 Nombre de messages : 163 Nombre de messages : 163
Age : 30
Date d'inscription : 27/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 25 Nov 2010, 12:41 Jeu 25 Nov 2010, 12:41 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  | |
| |
|
  | |
| | Olympiodiose |  |
|
