Olympiodiose

Petite faute de tape Majdouline ^^
C'est 17/6 + 1/6 pas 3/2+1/6 .

Pour l'exo on a :

Salut tous le monde ^^

Je poste cet exo pour faire bouger le topic un petit peut =P
C'est un peu facile mais bon ^^

Déterminez toutes les fonctions de l'ensemble des nombres réels dans
lui-même
telles que
f(x - f(y)) = f(f(y)) + xf(y) + f(x) - 1.

s=\frac{1*3}{3*5}+\frac{2*4}{5*7}+.......+\frac{(n-1)*(n+1)}{(2n-1)*(2n+1)}+......+\frac{1004*1006}{2009*2011}

slt tou le monde moi aussi j'ai passé le 2em test d'olymp mai le 4em exo je pense ke la solution de SYLPHAEN n'est pa just kar (apd) est strictement inferieur a 108
je peu vou dezmentre ca si vous voulez

ds dementrer

C'est la solution officielle -_-''

Sylphaen a écrit:

Déterminez toutes les fonctions de l'ensemble des nombres réels dans
lui-même
telles que
f(x - f(y)) = f(f(y)) + xf(y) + f(x) - 1.

Il serait temps de proposer ta solution..

On pose :
f(y)=x
L'équation devient :

f(0)=2f(x)+x²-1

On pose x=0

f(0)=2f(0)-1 d'où f(0)=1

Puis on trouve :
f(x)=1-x²/2

Sauf erreur ..

Le fait de poser puis 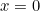suppose que 0 possède au moins un antécédent par 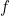. Ce qui nécessite d'être prouver..

Oui désolé j'avais pas remarquer >.<
Je vais rectifier ..

bjr les amis j'aime b1 savoir wech redo 3likom les resulta d'olymp

salut einstein20 mazal marado resulta d'olympiade wa9ila hta l dora tania

ah ok mercii kayt3etlo bezaf hado

oui khoya einstein kayt3atlo bache yalah ydzwo 3 dial marahil fl 3am kaml

Sylphaen a écrit:

Salut tous le monde ^^
Je poste cet exo pour faire bouger le topic un petit peut =P
C'est un peu facile mais bon ^^
Déterminez toutes les fonctions de l'ensemble des nombres réels dans
lui-même
telles que
f(x - f(y)) = f(f(y)) + xf(y) + f(x) - 1.

Voici ce que j'ai fait:
On souhaite trouver tous les applications de vers .
Et qui réalisent .
On pose .
On a .
Donc .
Donc .
Donc .
Donc .
Réciproquement, soit f la fonction définie par .
On a .
Donc .
Donc .==>(1)
Et on a .
Donc .==>(2)
De 1 et 2, on déduit que .
Donc la fonction est la seule à satisfaire les conditions.
P.S: J'attends vos remarques.

oui nmo , ta réponse est vrais ! meme le resultat , voila autre méthode :
posons que f(0)=n
x=y=0 ==> f(-n)=f(n)+n-1 (*) donc si n=0 ==> f(0)=f(0)-1 ==> absurde donc n#0
x=f(y) ==> n= 2f(x)+n²-1 (**)
(*) et (**) ==> f(x)= n+1-x²/2 (1)

y=0 ==> f(x-n)=f(n)+xn+n-1 ==> f(x-n)-f(x)=xn+n-1
donc tt réells s'écrit comme différence de 2 éléments dans Df
alors x=a-b
f(x)=f(a-b) =n - 1/2 x²
ce qui donne avec la relation 1 que n=1
alors f(x)=1 - 1/2x²
x |==> 1- 1/2x²
réciroque est facile !

Un exercice pour vous:
Dans un triangle, on connait les lonqueurs des trois médianes:
, , et .
Déterminez les longueurs a, b, et c des trois côtés BC, CA, et AB.
Bonne chance.

les côtés du triangle sont les 4/3 des médianes du triangle formé avec les médianes AA', BB' et CC'.
Sinon La formule de la médiane sous la forme m²_A = b²/2 + c²/2 - a²/4 permet d'écrire 3 équations d'inconnues a², b² et c² : c'est un système.

Tu en déduiras a, b et c.

Au plaisir

M.Marjani a écrit:

les côtés du triangle sont les 4/3 des médianes du triangle formé avec les médianes AA', BB' et CC'.
Sinon La formule de la médiane sous la forme m²_A = b²/2 + c²/2 - a²/4 permet d'écrire 3 équations d'inconnues a², b² et c² : c'est un système.
Tu en déduiras a, b et c.
Au plaisir

Bien, ce qui compte est la réponse.
J'attend une solution approfondie.

nmo a écrit:

Un exercice pour vous:
Dans un triangle, on connait les lonqueurs des trois médianes:
, , et .
Déterminez les longueurs a, b, et c des trois côtés BC, CA, et AB.
Bonne chance.

La réponse est ainsi:
Selon le théorème de la médiane,
On écrit AB²+AC²=2AA'²+(1/2)BC².
Donc c²+b²=2AA'²+(1/2)a².
Et aussi a²+b²=2CC'²+(1/2)c².
Et aussi a²+c²=2BB'²+(1/2)b².
Pour trouver a, b, et c, on doit résoudre le système suivant .
Soit .
Donc .
Donc .
Donc .
En sommant les trois lignes, on obtient .
Donc .
Donc .
Donc .
Donc .
On a d'après le système .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
On a par équivalence, le système suivant .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Les distances sont forcément positifs, alors a=5, b=6, c=7.
Sauf erreur.

Je présent un nouvel exercice:
Soit ABC un triangle dont les côtés sont a, b, et c.
p son demi-périmètre, r le rayon de son cercle inscrit, R celui de son cercle surconscrit.
Montrez que .
Bonne chance.

- Première partie :
.
Puisque , l'inégalité est aussi équivalente à .
En utilisant alors la formule de Héron, l'inégalité devient équivalente à .
a, b et c étant les longueurs de côtés d'un triangle, il est possible d'utiliser la substitution de Ravi : .
L'inégalité change alors de forme, et devient : , ce qui n'est qu'une simple application de l'IAG.

- Seconde partie :

Dijkschneier a écrit:

- Première partie :
.
Puisque , l'inégalité est aussi équivalente à .
En utilisant alors la formule de Héron, l'inégalité devient équivalente à .
a, b et c étant les longueurs de côtés d'un triangle, il est possible d'utiliser la substitution de Ravi : .
L'inégalité change alors de forme, et devient : , ce qui n'est qu'une simple application de l'IAG.
- Seconde partie :

Bien joué. Comme j'ai fait, vitement.
La deuxième a pris beaucoup de mon temps.
Un peu de reflexion, et tu trouves le résultat.

nmo a écrit:

Dijkschneier a écrit:

- Première partie :
.
Puisque , l'inégalité est aussi équivalente à .
En utilisant alors la formule de Héron, l'inégalité devient équivalente à .
a, b et c étant les longueurs de côtés d'un triangle, il est possible d'utiliser la substitution de Ravi : .
L'inégalité change alors de forme, et devient : , ce qui n'est qu'une simple application de l'IAG.
- Seconde partie :

Bien joué. Comme j'ai fait, vitement.
La deuxième a pris beaucoup de mon temps.
Un peu de reflexion, et tu trouves le résultat.

Je dis bien joué à Dijksheiner, et je vous présente nmo la solution du deuxiéme partie:

OA+OB>=AB , OA+OC>=AC , OB+OC>=BC
Posant: OA=OB=OC=R => 6R>=a+b+c <=> R>=(a+b+c)/6 (1)
Revenons à l'énoncé, on veut montrer que: P/3V3=<R/2
D'une autre maniére on veut montrer que: R>=2P/3V3 (R>=(a+b+c)/3V3)
Puisque: (a+b+c)/6>=(a+b+c)/3V3
Cela veux dire bien donc que: P/3V3=<R/2.

En déssinant la figure, l'EX devenait façile, je l'ai fais en 5 min environt.
Merci.

M.Marjani a écrit:

OA+OB>=AB , OA+OC>=AC , OB+OC>=BC
Posant: OA=OB=OC=R => 6R>=a+b+c <=> R>=(a+b+c)²/6 (1)

Il n'y a pas ici d'équivalence, mon cher.