| | Olympiodiose |  |
|
+31Dijkschneier SherlocK mizmaz reda-t smash stranger Emerson Perelman dima_amazigh Ayoub M-H EINSTEINIUM Sylphaen neohs noirouge majdouline soukki abdellah=einstein issam erriahi Thalès yassine-516 houssam110 marouan777 einstein20 darkpseudo albertmath otman1994 ayyoub Psi just-abdess radouane_BNE samix 35 participants |
|
| Auteur | Message |
|---|
abdellah=einstein
Maître

 Nombre de messages : 110 Nombre de messages : 110
Age : 31
Localisation : taroudant
Date d'inscription : 07/03/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 12:56 Ven 18 Déc 2009, 12:56 | |
| Bonjour  | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 13:10 Ven 18 Déc 2009, 13:10 | |
| Salam incorrect Abdellah vs n'avez pas compris la suite !!...elle formée comme sa : U_n=1/1.2 +1/2.3 +1/3.4 +...1/(n-1)(n)+1/n.(n+1)+....1/(2n-1).2n A_n =1/(n+1 ) +1/(n+2)+...1/2n et S=U_n+A_n et on a qq chose qyé évidente U_n=1-1/2n donc U_3=1-1/6 alors chez vs U_3=1/1.2 +1/2.3+1/5-1/6 =1/2-1/5 #1/6 ... et la preuve de cke je dis c kilsont écrit 1/1.2 +1/2.3 +...1/(2n-1)(2n) par exemple ici 1/1.2+1/2.3 donc ici dans le 1er nombre on a finit par 2 et dans le seconde o va commencer par 2 ... cherchez encore ...  | |
|
  | |
SherlocK
Maître

 Nombre de messages : 102 Nombre de messages : 102
Age : 31
Localisation : Khouribga, Maroc
Date d'inscription : 22/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 13:11 Ven 18 Déc 2009, 13:11 | |
| S=0   .... Il y a le contre exemple n=2 S=1/6 comme l'a dit Houssam donc c'est faux ! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 13:31 Ven 18 Déc 2009, 13:31 | |
| | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 13:45 Ven 18 Déc 2009, 13:45 | |
| Pour n on a : 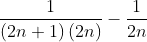 = 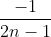 Donc la suite devient : 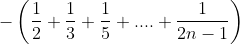 Et c'est la que j'ai remarqué qu'il y a un truc illogique dans ta suite je pense qu'elle s'ecri sous la forme qu'a dite sylphean au début dans ce cas ma réponse serai juste je pense !! | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 14:22 Ven 18 Déc 2009, 14:22 | |
| bonjour... j'interviens pour dire que S=0....en effet le deuxième terme n'était qu'une erreur de frappe c'est 1/3.4 et nn pas 1/2.3...c'est le troisième exo du 5eme test de l'olympiade 2009  ...j'ai cette olympiade comme j'ai sa solution ...si vous voulez je peux vous indiquer le lien de la solution....donc les solutions de Sylphaen et abdellah sont acceptables...... P.S.c'est juste ce que je vois...vous pouvez ignorer mon intervention  en tt cas comme remarque ..l'exo nous demande de calculer la différence entre deux sommes différentes ...on doit donc trouver une relation entre ces deux sommes...et si la suite est comme a dit houssam je crois pas pouvoir calculer cette somme car ya pas de relations entre ces deux suites..... | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 15:26 Ven 18 Déc 2009, 15:26 | |
| oué c cke je vois moi aussi car a la fin j'arrive a une suite qui n'a pa de sens !!
alors keske vou proposez kon fasse mnt??!!
Ps: c koi ces fautes la donnée a des éleves aux olympiades on espere kon tombrea po dans ce probleme car c suite est ecrite en arabe et en français :S | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 15:57 Ven 18 Déc 2009, 15:57 | |
| Exo de Sylphaen est en jeu sa solution est acceptée ! Indication : - Spoiler:
considérer la fonction f(x)=6x^3 /(1+x)^3
jposte la solution le soir !! A+ | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 17:22 Ven 18 Déc 2009, 17:22 | |
| On pose 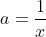 , 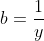 et 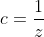 . On a alors 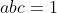 , et l'inégalité devient : (c+1)}&space;\geq&space;\frac{3}{4}&space;\Leftrightarrow&space;\sum&space;_{cyc}&space;\frac{a^{2}}{(b+1)(c+1)}&space;\geq&space;\frac{3}{4}) Or, on sait que (c+1)}%20\geq%20\frac{(a+b+c)^{2}}{\sum%20_{cyc}(b+1)(c+1)}%20=%20\frac{(a+b+c)^{2}}{2(a+b+c)+(ab+ac+bc)+3}) d'après C.S (aussi appelé le lemme de Titu, lorsqu'il est présenté sous cette forme). Mais ^{2}}{2(a+b+c)+(ab+ac+bc)+3}&space;\geq&space;\frac{3}{4}&space;\Leftrightarrow) ^{2}&space;\geq&space;3(2(a+b+c)+(ab+ac+bc)+3)&space;\Leftrightarrow) (a+b+c-3)&space;+&space;((a+b+c)^{2}&space;-&space;3(ab+ac+bc))&space;+&space;((a+b+c)^{2}&space;-&space;9)&space;\geq&space;0) Qui est facilement démontrable. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 18:19 Ven 18 Déc 2009, 18:19 | |
| bonsoir.... y a des solution plus simples à ce problème....à toi Dijkschneier ,poste nous un exo  | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 18:22 Ven 18 Déc 2009, 18:22 | |
| bonsoir oué c sa .. je savé po la Lemme de titu
ma démosntrastion se basé sur chebychev , les moyennes et la fonction ke jé déja cité !!
a toi !! | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 18:26 Ven 18 Déc 2009, 18:26 | |
| Solution ( sauf erreur biensure) on a (z+1)}\geq&space;\sum&space;\frac{x^{4}}{x(y+1)(z+1)}\geq&space;\frac{(x^{2}+y^{2}+z^{2})^{2}}{\sum&space;x+xy+xz+xyz}=&space;\frac{(x^{2}+y^{2}+z^{2})^{2}}{x+y+z+2(xy+yz+zx)+3xyz}=A) c'est facile de montrer que 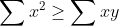 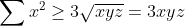 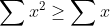 donc ^{2}}{4(\sum&space;x^{2})}\geq&space;\frac{(\sum&space;x^{2})}{4}\geq&space;\frac{3}{4})
Dernière édition par just-abdess le Sam 19 Déc 2009, 13:33, édité 1 fois | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 19:02 Ven 18 Déc 2009, 19:02 | |
| aussi je propose une solution....sauf erreur... l'inégalité est équivalente à: \geq%203(x+y+z+xy+yz+zx+2)) par symétrie des rôles supposons que x>=y>=z par Chebyshev on a donc:  CQFD | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 19:50 Ven 18 Déc 2009, 19:50 | |
| bonsoir just abdess:
pour l'erreur que tu as commise dans ta démonstration...est du genre logique...en effet:
on veut démontrer cette proposition: (∀x£]0,+∞[):f(x)=x
donc la négation c'est:(∃x£]0,+∞[):f(x)≠x
il existe un x....
donc t'as fait il existe un x de ]0,+∞[:f(x)≠x<=>(∃x£]0,+∞[):f(x)>x ou (∃x£]0,+∞[):f(x)<x
donc on a f(x)<x ...mais ça ne nous permet pas d'écrire que f(y)<y...car on a il existe un x de IR+ et nn pas pour tout x de IR+....ainsi ton raisonnement est incorrect..... | |
|
  | |
einstein20
Maître

 Nombre de messages : 102 Nombre de messages : 102
Age : 31
Localisation : oujda
Date d'inscription : 14/04/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 20:05 Ven 18 Déc 2009, 20:05 | |
| bah slt tou l'monde voisi un exo d'olymp:
calculer A ;A=1/1.2 + 1/3.4 +...1/(2n-1)2n - 1/n+1 -1/n+2 -...-1/2n | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 22:31 Ven 18 Déc 2009, 22:31 | |
| pourtant je propose la solution suivante pour le problème de abdellah: donc pour a=b=x=y=1 on aura f(1)=1 pour a=b=x=y on aura: [f(x)]²=f(x²) alors notre relation devient: +f(y^2)}{f(a^2)+f(b^2)%20}=\frac{x^2+y^2}{a^2+b^2}<br />) donc pour x²=X et y²=Y et a²=A et b²=B on aura : +f(y)}{f(a)+f(b)%20}=\frac{x+y}{a+b}) avec V(xy)=V(ab)<=>xy=ab pour y=1 on aura ab=x alors l'équation devient: +1}{f(a)+f(b)%20}=\frac{ab+1}{a+b}) <=>a+b+a.f(ab)+b.f(ab)=f(a)+f(b)+ab.f(a)+ab.f(b) pour a=b on aura: 2a+2a.f(a²)=2f(a)+2a²f(a) or f(a²)=[f(a)]² alors: a+a.[f(a)]²=f(a)+a²f(a) <=>(a-f(a))(1-a.f(a))=0 d'où f(a)=a ou f(a)=1/a alors (∀x£IR+*) f(x)=x
(∀x£IR+*) f(x)=1/x | |
|
  | |
SherlocK
Maître

 Nombre de messages : 102 Nombre de messages : 102
Age : 31
Localisation : Khouribga, Maroc
Date d'inscription : 22/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 22:34 Ven 18 Déc 2009, 22:34 | |
| - einstein20 a écrit:
- bah slt tou l'monde voisi un exo d'olymp:
calculer A ;A=1/1.2 + 1/3.4 +...1/(2n-1)2n - 1/n+1 -1/n+2 -...-1/2n C'est déjà posté  | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Sam 19 Déc 2009, 13:33 Sam 19 Déc 2009, 13:33 | |
| Re oui ta raison majdouline ma solution est fausse , merci ^^ | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Sam 19 Déc 2009, 17:17 Sam 19 Déc 2009, 17:17 | |
| bonsoir  ..... on attend encore ton exo Dijkschneier!!!!!!!!!!!!!!! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Sam 19 Déc 2009, 18:15 Sam 19 Déc 2009, 18:15 | |
| - majdouline a écrit:
- bonsoir
 ..... .....
on attend encore ton exo Dijkschneier!!!!!!!!!!!!!!! J'ai pas vraiment d'exercice sur la conscience à proposer.. Je vous laisse la main. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 21 Déc 2009, 20:34 Lun 21 Déc 2009, 20:34 | |
| Comme tous le monde est absent je pose cette exo ^^ Soit a,b,c>0 M.Q  | |
|
  | |
issam erriahi
Expert sup

 Nombre de messages : 1102 Nombre de messages : 1102
Age : 34
Date d'inscription : 31/12/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 24 Déc 2009, 11:21 Jeu 24 Déc 2009, 11:21 | |
| | |
|
  | |
issam erriahi
Expert sup

 Nombre de messages : 1102 Nombre de messages : 1102
Age : 34
Date d'inscription : 31/12/2008
 | |
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 24 Déc 2009, 14:11 Jeu 24 Déc 2009, 14:11 | |
| je poste la solution de l'inégalité :  par Am-Gm on a: }{4(ab+bc+ca)}+\frac{2(ab+bc+ca)}{3(a+b)(b+c)}) la somme cyclique donne :  il est bien connu que (a+b)(b+c)(c+a)≥8abc ...alors : (a+c)(b+c)}\leq%20\frac{17}{6}+\frac{1}{6}=3) CQFD...
Dernière édition par majdouline le Jeu 24 Déc 2009, 20:02, édité 1 fois | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 24 Déc 2009, 14:40 Jeu 24 Déc 2009, 14:40 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  | |
| |
|
  | |
| | Olympiodiose |  |
|
