| | Olympiodiose |  |
|
+31Dijkschneier SherlocK mizmaz reda-t smash stranger Emerson Perelman dima_amazigh Ayoub M-H EINSTEINIUM Sylphaen neohs noirouge majdouline soukki abdellah=einstein issam erriahi Thalès yassine-516 houssam110 marouan777 einstein20 darkpseudo albertmath otman1994 ayyoub Psi just-abdess radouane_BNE samix 35 participants |
|
| Auteur | Message |
|---|
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 17:49 Jeu 17 Déc 2009, 17:49 | |
| OUé mnt sava  belle solution!! dans la mienne yavé 6 cas ^^ POSTE un Exo!! | |
|
  | |
samix
Expert grade2

 Nombre de messages : 322 Nombre de messages : 322
Age : 30
Localisation : Oujda
Date d'inscription : 02/12/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 18:04 Jeu 17 Déc 2009, 18:04 | |
| Solution :
on a : x=[x]+p avec p £ [0,1]
donc l'équation est équivalente à :
4x²-40(x-p)+51=0
4x²-40x+40p+51=0
delta=40²-16(40p+51)=784-640p
x=( 40+V(784-640p) ) / 8 où x=( 40-V(784-640p) ) / 8
[x]=( 40+V(784-640p) ) / 8 -p où [x]=( 40-V(784-640p) ) / 8 -p
1er cas :
puisque : p £[0,1] alors : 5,5 ≤( 40+V(784-640p) ) / 8 -p ≤ 8,5
donc [x]=6 où [x]=7 où [x]=8 en remplacent on obtiens : x= V229 /2 ,
x=V269 / 2 , V189/2
2eme cas :
on a :
1 ≤( 40-V(784-640p) ) / 8 -p ≤ 3,5
d'où [x]=1 , [x]=2 , [x] = 3
si [x]=1 impossible , si [x]=2 alors x=V29/2 , si [x]=3 impossible
Conclusion : x £ {V229/2,V269/2,V189/2,V29/2} | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 18:11 Jeu 17 Déc 2009, 18:11 | |
| Bonsoir tout le monde
@ Samix c la meme méthode ke jé fait mais a la fin il fallé vérivier tes solution
ta dit que [x]=3==> x=V69/2 =4.153....
ckiné pa logike car on dit ke [x]=3
....
On attend ton exo Majdouline!! | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 20:25 Jeu 17 Déc 2009, 20:25 | |
| je crois qu'il est temps de retourner aux inégalités  ...je propose une facile qui ne nécessite pas l'utilisation des théorèmes .. problème proposé:soient a b et c les longueurs des cotés d'un triangle tel que :a+b+c=2 ;prouver que:
a²+b²+c²+2abc<2ENJOY  P.S.la solution peut être rédigée en 2 lignes P.S.la solution peut être rédigée en 2 lignes | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 21:42 Jeu 17 Déc 2009, 21:42 | |
| Bsr SOlution du Probleme (Sauf erreur) avec l'inégalité triangulaire on peut aisément prouver que a,b,c<1 on a a²+b²+c²+2abc<2 <==> (a+b+c)²+2abc<2+2ab+2ac+2bc <==>2+abc<1+ab+ac+bc <==>2+abc<1+a(2-a)+bc <==>(1-a)²<bc(1-a) <==> 1<bc+a <==> b+c<bc+1 <==> 0<(1-c)(1-b) ckyé vré !! PS: c en 2 lignes  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 21:52 Jeu 17 Déc 2009, 21:52 | |
| correct à toi houssam  | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 22:33 Jeu 17 Déc 2009, 22:33 | |
| Bonsoir!! j'ai un grand problem avec le latex je peu pa afficher l'image alors jlé enregistré et eberger dans un autre site bon Probleme Proposécalculer : 
Dernière édition par houssam110 le Jeu 17 Déc 2009, 23:02, édité 1 fois | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 22:58 Jeu 17 Déc 2009, 22:58 | |
| Par symètrie : a≤b≤c Donc c≥2/3 c²≥4/9 3c²≥a²+b²+c² c 3≥abc 4/3≥a²+b²+c² 16/27≥2abc 4/3+16/27=52/27<2 donc a²+b²+c²+2abc≤52/27<2 Désolé pour le retard j'avais po vu vu que la page a tourné  | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 23:11 Jeu 17 Déc 2009, 23:11 | |
| bonsoir
non sylphaen c faux!!...
3c²>=a²+b²+c² et 3c²>=4/3 nimplique po 4/3>=a²+b²+c² | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 23:17 Jeu 17 Déc 2009, 23:17 | |
| Oups ! ><' C'était du vite fait  Sinon pour ton exo c'est : 1/1.2 +1/3.4 pas 1/1.2 +1/2.3 | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 23:21 Jeu 17 Déc 2009, 23:21 | |
| c ckilia dans la feuille !!
c un olym de l'année derniere (5eme contrle) | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 23:27 Jeu 17 Déc 2009, 23:27 | |
| | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 23:31 Jeu 17 Déc 2009, 23:31 | |
| Salut tout le monde
cet exo est copié mot par mot
et le but de cette ecriture c dire ke le dir le dernier terme contient 1/(2n(2n-1) et celui kyé avant 1/(2n-1)(2n-2)... | |
|
  | |
yassine-516
Maître

 Nombre de messages : 128 Nombre de messages : 128
Age : 31
Date d'inscription : 11/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 23:33 Jeu 17 Déc 2009, 23:33 | |
| | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 23:37 Jeu 17 Déc 2009, 23:37 | |
| prend n=1 on aura 1/1.2 OK
prend n=2 on aura 1/3.4 Pas Ok tu vois ? | |
|
  | |
yassine-516
Maître

 Nombre de messages : 128 Nombre de messages : 128
Age : 31
Date d'inscription : 11/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 23:39 Jeu 17 Déc 2009, 23:39 | |
| C'est ce que j'ai remarqué moi aussi mais 1/2.3 est juste si n=3/2
c'est pourquoi je ve savoir à quel essemble appartient n | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 23:44 Jeu 17 Déc 2009, 23:44 | |
| Beh c'est IN évidement ^^ | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 17 Déc 2009, 23:46 Jeu 17 Déc 2009, 23:46 | |
| Déjà on a 1/[(2n-1)2n] = 1/(2n-1) - 1/(2n) | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 00:01 Ven 18 Déc 2009, 00:01 | |
| J'ai trouvé 0 !
Je poste ma soluce | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 01:10 Ven 18 Déc 2009, 01:10 | |
| On pose S(n) :  Et : U(n):  On : S(n) = 1 -1/2 +1/3 -1/4 .... On remarque que l'inverse des chiffres inverse est positive ! Alors dans l'addition de S(n)+U(n) tous les inverse des impaires dérrières 1/n+1 vont disparaître (1). Alors on gardera uniquement les paires de U(n) et les paires qui sont derrière 1/n+1 de S(n). Aussi on peut remarquer que la somme deviendra ainsi : S(n)+U(n)= [img]http://latex.codecogs.com/gif.latex?1-%5Cfrac%7B1%7D%7B2%7D+%5Cfrac%7B1%7D%7B3%7D-%5Cfrac%7B1%7D%7B4%7D+%5Cfrac%7B1%7D%7B5%7D-%5Cfrac%7B1%7D%7B6%7D.....-%5Cfrac%7B1%7D%7Bn%7D-%5Cfrac%7B1%7D%7Bn+2%7D-%5Cfrac%7B1%7D%7Bn+4%7D...-%5Cfrac%7B1%7D%7B2n%7D+[%20-%5Cfrac%7B1%7D%7Bn+2%7D-%5Cfrac%7B1%7D%7Bn+4%7D....-%5Cfrac%7B1%7D%7B2n%7D][/img] Ici j'ai pris n paire mais ca n'importe pas S(n)+U(n)=  Puis on sommant chacun avec son double on aura 0 :p J'ai pas fini mais bon maintenant je vais me coucher lol | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 11:11 Ven 18 Déc 2009, 11:11 | |
| Je l'ai fait par récurrence : On suppose que c'est égal à 0 ! Pour 1 ca marche car : 1/1.2 -1/(1+1) =0 On suppose que : 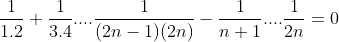 Et montrons que : 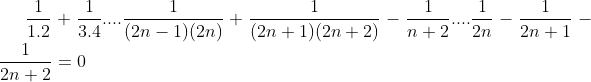 | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 11:22 Ven 18 Déc 2009, 11:22 | |
| Ce qui veut dire :  Ce qui équivaut : 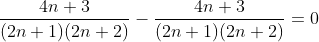 Ce qui est vrait : Désolé pour le double messages j'avais des blèmes avec le latex >< Si c'est correcte je laisse cet exo : Soit x,y,z>0 tels que xyz=1 MQ :  | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 11:34 Ven 18 Déc 2009, 11:34 | |
| Salut
c faux sylphaen !!
ta fait des fuites dans les termes qui suivent par exemple le nombre qui suit 1/(2n)(2n-1) c 1/2n(2n+1)
en + sa se voit que c voit un contre exemple peut te la montrer en 1/8 lignes ^^
n=2...
cherchez encore... | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 11:37 Ven 18 Déc 2009, 11:37 | |
| Je pense pas regarde pour n on a :
1/(2n-1)2n pour n+1 on : 1/(2(n+1)-1)(2(n+1))=1/(2n+1)(2n+2)
Et pour n=2 on a :
1/2 +1/(3.4) -1/3-1/4 = 1/2 +1/12 - 7/12 =0 | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 11:46 Ven 18 Déc 2009, 11:46 | |
| pour n=2 S_2=1/2 +1/2.3 +1/3.4-1/3-1/4 =1/6 ta po bien compris la suite !! c pa assez facile cherche encore  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  | |
| |
|
  | |
| | Olympiodiose |  |
|
